
- •1.Основные понятия и формулы комбинаторики.
- •2.Случайные события и действия над ними. Виды событий
- •3. Аксиоматическое определение вероятности
- •6.Понятие дискретной случайной величины. Закон распределения дискретной одномерной случайной величины. Функция распределения f(X), ее свойства.
- •7.Числовые характеристики дискретной случайной величины.
- •8.Схема Бернулли. Формула Бернулли. Локальная и интегральная теорема Муавра-Лапласа
- •9.Биномиальное распределение.
- •10.Понятие непрерывной случайной величины. Функция распределения, ее свойства. Функция плотности распределения вероятностей, ее свойства. Числовые характеристики непрерывных случайных величин.
- •11.Распределение Пуассона
- •12.Нормальный закон распределения. Числовые характеристики нормального закона. Свойства нормальной кривой. Правило 3-х сигм, его практическое применение.
- •14.Дискретный вариационный ряд и его числовые характеристики
- •15.Интервальный статистический ряд и его числовые характеристики.
- •16.Статистическое оценивание параметров распределения по выборке. Точечные оценки параметров распределения
- •18.Статистическая проверка гипотез. Мощность критерия. Критические области
- •19.Статистическая проверка гипотез. Ошибки первого и второго родов.
- •Уровень значимости
- •Мощность и ошибка второго рода
- •20.Двумерная случайная величина. Закон распределения. Условные законы распределения.
- •21.Двумерная случайная величина. Числовые характеристики двумерной случайной величины.
- •2 Типа взаимосвязей между х и у:
3. Аксиоматическое определение вероятности
Пусть
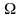 - пространство элементарных исходов
некоторого испытания, а
- пространство элементарных исходов
некоторого испытания, а
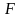 -
-
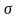 -алгебра
событий, определенная на этом пространстве.
Каждому событию
-алгебра
событий, определенная на этом пространстве.
Каждому событию
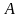 множества
ставится в соответствие величина
множества
ставится в соответствие величина
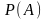 ,
называемая вероятностью события
и удовлетворяющая следующим условиям:
,
называемая вероятностью события
и удовлетворяющая следующим условиям:
А1.
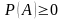 .
.
А2. Вероятность
достоверного события
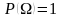 .
.
А3. Если в
последовательности событий
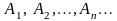 события попарно несовместны (т.е.
события попарно несовместны (т.е.
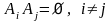 ),
то
),
то
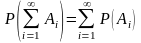 .
.
Таким образом,
вероятность есть функция
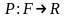 ,
удовлетворяющая условиям А1-А3, или, как
говорят, нормированная (вероятностная)
мера, заданная на множестве
.
Аксиомы А1-А3 называются аксиомами теории
вероятностей.
,
удовлетворяющая условиям А1-А3, или, как
говорят, нормированная (вероятностная)
мера, заданная на множестве
.
Аксиомы А1-А3 называются аксиомами теории
вероятностей.
Заметим, что аксиома А3 эквивалентна двум следующим аксиомам (без доказательства):
А4. Если
и
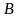 несовместны, то
несовместны, то
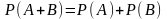 .
.
А5. Если
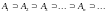 и
и
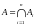 ,
или
,
или
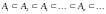 и
и
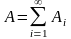 ,
то
,
то
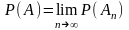 .
.
Определение
3. Тройка
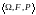 ,
где
- пространство элементарных исходов,
-
-алгебра
его подмножеств, а
,
где
- пространство элементарных исходов,
-
-алгебра
его подмножеств, а
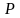 вероятностная мера на
называется вероятностным
пространством.
4.Теорема
сложения и умножения вероятностей.
Независимые события. Условная вероятность
вероятностная мера на
называется вероятностным
пространством.
4.Теорема
сложения и умножения вероятностей.
Независимые события. Условная вероятность
Теорема 1. (Сложения вероятностей)
Вероятность суммы двух совместных событий и равна сумме вероятностей этих событий без вероятности их совместного наступления
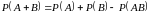 .
.
Вероятность суммы несовместных событий рвана сумме их вероятностей, т.е.
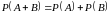 .
.
.
События и называются независимыми, если вероятность не зависит от того, произошло событие или нет.
Событие называется зависимым от события , если вероятность события зависит от того, произошло или не произошло событие .
Вероятность
события
,
вычисленная
при условии, что
имело место, называется условной
вероятностью
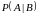 .
.
Теорема 2. (Умножения вероятностей)
Вероятность произведения двух зависимых событий и равна произведению вероятности одного их этих событий на условную вероятность другого, при условии, что первое наступило:
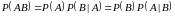 .
.
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
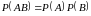 .
.
Определение
1. Вероятность события
,
вычисленная при условии, что имело место
событие
,
называется условной вероятностью
события
относительно события
и обозначается
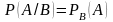 .
.
Легко заметить,
используя классическое или геометрическое
определение вероятности, что
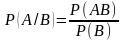 (см. рис14), однако для произвольного
пространства
,
доказать это невозможно, поэтому в
аксиоматической теории понятие условной
вероятности дается как определение.
(см. рис14), однако для произвольного
пространства
,
доказать это невозможно, поэтому в
аксиоматической теории понятие условной
вероятности дается как определение.
Определение 2. Условной вероятностью события относительно события называется величина, равная
,
(при условии
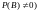 .
5.Формула
полной вероятности
.
5.Формула
полной вероятности
Если событие А может
произойти только при выполнении одного
из событий ![]() ,
которые образуют полную группу
несовместных событий, то вероятность
события Авычисляется по формуле
,
которые образуют полную группу
несовместных событий, то вероятность
события Авычисляется по формуле
![]() .
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу
несовместных событий
,
вероятности появления которых ![]() .
Событие А может произойти только
вместе с каким-либо из событий
,
которые будем называть гипотезами.
Тогда по формуле полной вероятности
.
Событие А может произойти только
вместе с каким-либо из событий
,
которые будем называть гипотезами.
Тогда по формуле полной вероятности
Если событие А произошло, то это может изменить вероятности гипотез .
По теореме умножения вероятностей
![]() ,
,
откуда
![]() .
.
Аналогично, для остальных гипотез
![]()
Полученная формула называется формулой
Байеса (формулой Бейеса). Вероятности
гипотез![]() называются апостериорными
вероятностями, тогда как
называются апостериорными
вероятностями, тогда как ![]() - априорными
вероятностями.
- априорными
вероятностями.
