21.Двумерная случайная величина. Числовые характеристики двумерной случайной величины.

Пусть (x , h ) - двумерная случайная величина, тогда M(x , h )=(M(x ), M(h )), т.е. математическое ожидание случайного вектора - это вектор из математических ожиданий компонент вектора.

Если (x , h ) - дискретный случайный вектор с распределением

 

	y1	y2	...	ym
x1	p11	p12	...	p1m
x2	p12	p12	...	p2m
...	...	...	pij	...
xn	pn1	pn2	...	pnm

 

то математические ожидания компонент вычисляются по формулам:

,  .

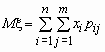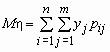Эти формулы можно записать в сокращенном виде.

Обозначим 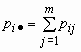  и  , тогда   и  .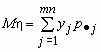

Если p_(x , h )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины (x , h ), то

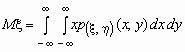 и  .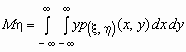

Поскольку 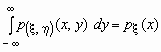  -плотность распределения случайной величины x , то 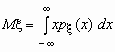 и, аналогично,  .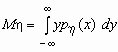

Дисперсия

 Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.

Если (x , h ) - двумерная случайная величина, то

Dx = M(x - Mx )² = Mx ² - M(x )², Dh = M(h - Mh )² = Mh ² - M(h )².

Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.

 Условное математическое ожидание

 Между случайными величинами может существовать функциональная зависимость. Например, если x - случайная величина и h =x ², то h - тоже случайная величина, связанная с xфункциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.

Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.

Для двумерного дискретного случайного вектора (x , h ) с распределением

Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov(x , h ). Ковариацию вычисляют по формулам cov(x , h )=M[(x - Mx )(h - Mh )] = M(x h) - Mx Mh .

Если случайные величины x и h независимы, то cov(x ,h )=0.

Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.

Свойства ковариации:

cov(x , x ) = Dx ;

Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции  . 22.Понятие функции регрессии.

Для количественного описания взаимосвязей между экономическими переменными в статистике используют методы регрессии и корреляции.

Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х.

Уравнение регрессии выражает среднюю величину одного признака как функцию другого.

Функция регрессии - это модель вида у = л», где у - зависимая переменная (результативный признак); х - независимая, или объясняющая, переменная (признак-фактор).

Линия регрессии - график функции у = f (x).