Мощность и ошибка второго рода

Снизить вероятность ошибки второго рода заметно труднее. Как правило, ее можно уменьшить, если увеличить число анализируемых наблюдений. Поэтому так необходимы большие выборки. Методы проверки гипотезы, обладающие таким свойством, называют состоятельными. Статистики добиваются такого результата математическими средствами, разрабатывая специальные алгоритмы проверки гипотезы.  .

Если выборка маленькая (часто в качестве границы между большой и маленькой выборкой берут пороговое значение 30 наблюдений), проверить гипотезу удастся. Платой за малый размер будет неприемлемо большая вероятность ошибки второго рода. Большинство практиков, работающих с маленькими выборками, думают, что смогут преодолеть эту трудность, если будут игнорировать ошибку второго рода, вовсе не обращать внимания на нее. Профессиональные статистики в таких ситуациях часто увеличивают уровень значимости (например, до 0.15 или 0.2), чтобы сделать вероятности ошибок первого и второго рода сопоставимыми.

20.Двумерная случайная величина. Закон распределения. Условные законы распределения.

Пусть на вероятностном пространстве   заданы две случайные величины:  . Каждому элементарному событию  ставится в соответствие упорядоченная пара значений   случайных величин  .

Упорядоченную пару   двух одномерных случайных величин   называют двумерной случайной величиной.

Двумерную случайную величину называют также случайным двумерным вектором, случайной двумерной точкой, системой двух случайных величин. Одномерные случайные величины   называются компонентами двумерной случайной величины  .

Функцией распределения   двумерной случайной величины   называется вероятность произведения событий   и  , определенная для любых вещественных  :  . (1)

Функция   для краткости называется двумерной функцией распределения.

Геометрический смысл равенства (1): функция   есть вероятность того, что случайная точка   попадет в бесконечный квадрат с вершиной в точке  ; точка   будет левее и ниже этой вершины.

Свойства двумерной функции распределения

1.  .

2.  ,  .

3.  .

4.  ;

. (2)

5.   неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.

Формулы (2) означают, что из функции распределения двумерной случайной величины можно получить функции распределения ее одномерных компонент.

Используя функцию распределения, можно найти вероятность попадания случайной точки в прямоугольник  :

.

Дискретная двумерная случайная величина

Двумерная случайная величина   называется дискретной, если множество ее значений   – конечное или счетное.

Закон распределения вероятностей двумерной дискретной случайной величины   можно задать формулой

. (3)

События   образуют полную группу событий, поэтому сумма всех вероятностей

   равна 1, т.е.  .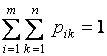 

Условным законом распределения дискретной случайной величины   при   называется множество значений   ( ) и условных вероятностей  ,  , …,  , вычисленных по формулам

,  .

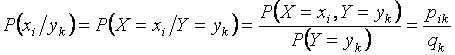Аналогично строится условный закон распределения дискретной случайной величины   при  , где условные вероятности   ( ) вычисляются по формулам

,  .

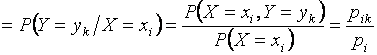Сумма вероятностей условного распределения равна единице.