Учитывая подвижности катионов и анионов,

V=v*F и U=u*F

получаем заданное выражение для разной степени диссоциации электролитов.

25. Основные положения теории сильных электролитов

Дебая-Хюккеля.

Эти представления сформулированы в виде идеи о наличии вокруг каждого иона ионной атмосферы из противоположно заряженных ионов. Ее плотность макс. у центра, с удалением от него ↓. На некотором расстоянии, которое можно считать границей ионной атм., кол-во ионов каждого знака одинаково. Термодинамические св-ва р-ров электролитов теория связывает с параметрами ионной атм. – ее размером и плотностью.

1. Электролит в растворе диссоциирован полностью, и кон-ция ионов рассчитывается по аналитической кон-ции электролита.

2. Распределение ионов в ионной атмосфере подчиняется классич. статике, а сама ионная атмосфера рассматривается как непрерывная среда.

3. Из всех видов взаимодействия учитывая только электростатическое взаимодействие ионов. Растворителюлю отводится роль среды с некоторой диэлектрической проницаемостью.

4. Диэлектрическая проницаемость р-ра принимается равной диэлектрической проницаемости чистого растворителя.

5. Из всех свойств ионов учитывается только заряд.

26. Что такое ионная атмосфера, релаксационное и электрофоретическое торможение?

Ионная атмосфера

Если мысленно выделить в разбавленном растворе сильного электролита один центральный ион, то ионы противоположного знака будут чаще наблюдаться около него, чем ионы с одноименным зарядом. Такое статистическое распределение ионов устанавливается под влиянием 2-х факторов:1) электростатических сил притяжения и отталкивания; 2) теплового движения ионов. В результате вокруг центрального иона устанавливается некоторое промежуточное статистическое распределение ионов – ионная атмосфера.

Электрофоретическое торможение. При наложении на раствор электрического поля центральный ион и его ионная атмосфера, обладающие противоположными по знаку зарядами, движутся в противоположных направлениях. Поскольку ионы гидратированы, то движение ионов движение центрального иона происходит в среде, перемещающейся ему навстречу. Поэтому движущийся ион находится под влиянием дополнительной тормозящей силы, что приводит к снижению его скорости.

Релаксационное торможение. Ионная атмосфера обладает центральной симметрией. При движении иона в электрическом поле симметрия нарушается, что связано с разрушением атмосферы в одном положении иона и формированием ее в другом, новом. Этот процесс происходит с конечной скоростью с течением некоторого времени – временем релаксации. Вследствие этого ионная атмосфера теряет центральную симметрию, и позади движущегося иона всегда будет некоторый избыток заряда противоположного знака. Возникающие при это силы электрического притяжения будут тормозить движение иона.

Силы релаксационного и электрофоретич. торможения

• определяются ионной силой раствора, природой растворителя и температурой.

• ↑ с ↑ концентрации р-ра при постоянстве прочих условий

27. В чем состоит эффект Вина? Что такое дисперсия электропроводности?

Эффект Вина

В постоянных электрических полях достаточно высокой напряженности (10⁴-10⁵ В/см)

Ионы движутся настолько быстро, что ионная атмосфера не успевает образовываться, вследствие чего практически отсутствуют эффекты торможения, а λ стремится к λ^∞.

В слабых электролитах эффект Вина вызывается также смещением диссоциативного равновесия в сильном электрическом поле в сторону образования ионов.

Дисперсия электропроводности (частотный эффект). При увеличении частоты переменного тока выше некоторого значения наблюдается увеличение электропроводности, т.к. при достаточно высокой частоте взаимные смещения иона и ионной атмосферы настолько малы, что ионная атмосфера практически симметрична.

Частота переменного тока, при которой можно ожидать возрастания электропроводности, - это величина, обратная времени релаксации

Следовательно должен исчезнуть эффект релаксационного торможения.

(Эффект Вина возникает при полном уничтожении ионной атмосферы, а следовательно и обоих эффектов торможения. Частотный эффект объясняется лишь исчезновеним ионной атмосферы. Опыт показывает, что последний эффект прим. в 3 раза слабее, чем эффект Вина, т.е. электрофоретический эффект в 2 раза сильнее эффекта релаксации)

28. Активности и коэффициенты активностей электролитов. Методы их определения и вычисления.

Активность связана с химическим потенциалом компонента раствора уравнением:

Индекс х указывает, что активность относится к раствору, в котором концентрация вещества выражена в молярных долях. Активность также иногда называют эффективной или действующей концентрацией.

Коэффициент активности – мера отклонения свойств раствора от св-в идеального раствора той же концентрации.

, где γ – мольный коэф. активности,

Возможны сопоставления активностей компонентов с концентрациями, выраженными в других единицах:

• мольно-объемные концентрации (с)

, где f – мольный коэффициент активности

• моляльность (m)

где γ’ – практический коэффициент активности

В общем случае свойства различных ионов в растворе неодинаковы и можно ввести и рассмотреть термодинамические функции для ионов различного типа:

1. Рассмотрим 2-х компонентный раствор, состоящий из растворителя и соли, диссоциирующей по уравнению:

2. Хим. потенциал: -

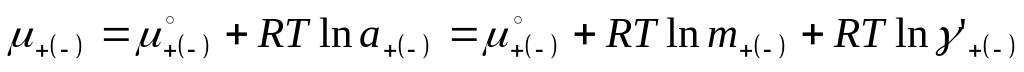(2 уравнения К⁺ и А^-)

3. Сделаем предположения:

- взято 1000г растворителя, n₁=1000/M₁, n₂=m – моляльность

- электролит диссоц. нацело:

- T,P = const,  по ур-ю Гиббса-Дюгема (изм-е хим. потенц-ов комп-ов р-ра при изм-ии состава р-ра):

- вычтем из 1-го 2-ое:

- введем среднюю ионную активность , где ;

- опытным путем получают a₂ и определяют a_ по ур-ю;

- вводят сред. ион. коэф. активности _ и срен. ион. моляльность m_:

;

- можно выразить практич.коэф.актив.

• Определение активности летучего вещества по парциальному давлению его пара.

Из уравнений: р₁=р*₁а₁, р₂=р*₂а₂, (где р₁ – парциальное давление пара растворителя над раствором, р*₁ – давление пара над жидким растворителем; р₂, р*₂ – соответственно для растворенного вещества) получаем

(индекс 1 указывает номер выбранного стандартного состояния)

Для определения γ твердого растворенного вещества выбираем второе стандартное состояние

(у – вспомогательная расчетная величина, К₂ – константа Генри)

Получаем:

(где у=у₀ при х₂→0 находят графическим способом).

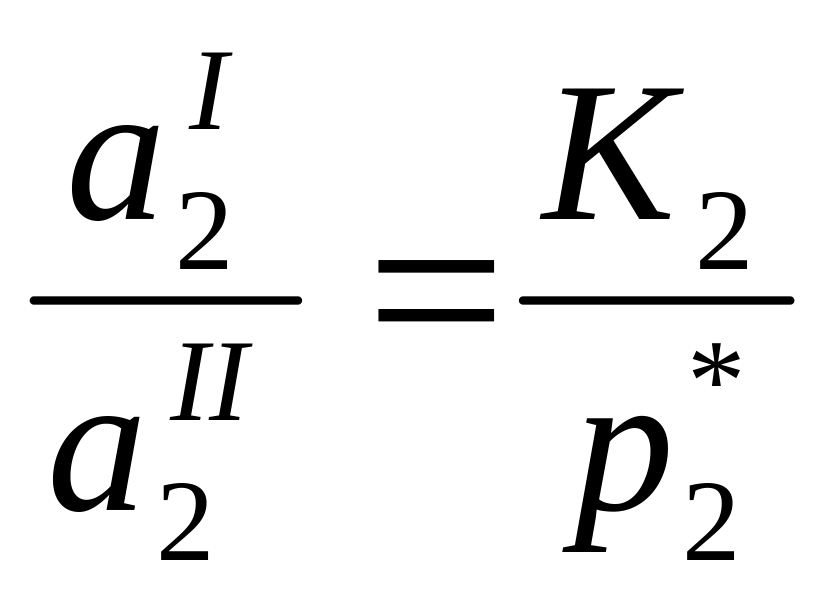
• Определение активности растворенного вещества по давлению пара растворителя.

Из уравнения Гиббса-Дюгема:

Интегрирование дает: ,

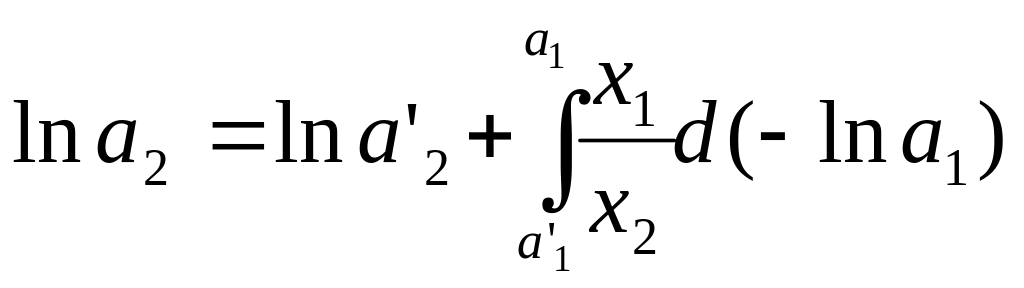где а’₁ и a’₂ – активности растворителя и растворенного вещества при составе раствора х'₂, они должны быть известны.

Также можно проинтегрировать уравнение Гиббса-Дюгема, выраженное через γ:

Активность а₁ определяют по давлению пара над растворами разного состава. Интеграл вычисляют графически.

• Определение активности растворенного вещества по коэфф. распределения.

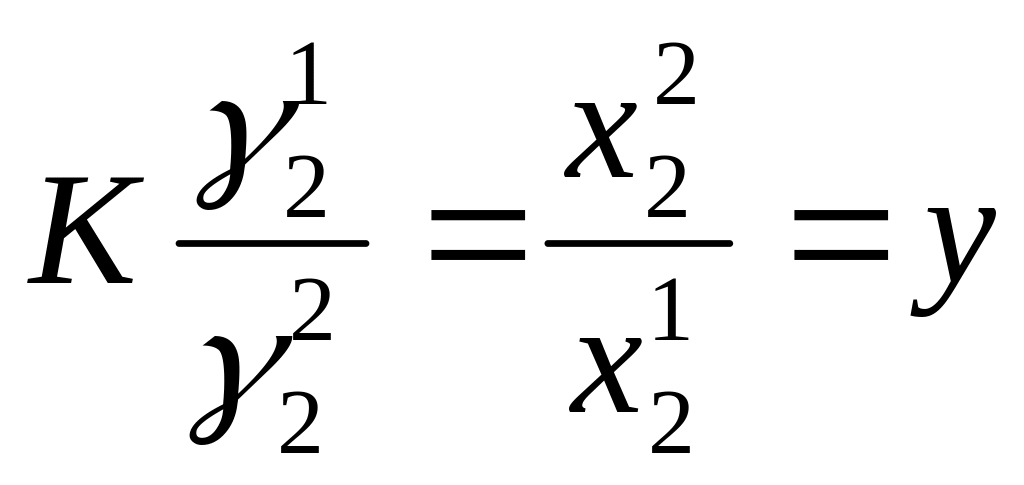
(где К – коэф. распределения, γ¹₂, γ²₂ - коэффициенты активности растворенного вещества в первом и втором растворителях, х¹₁, х²₂ - концентрации растворенного вещества в первом и втором растворителях).

а и γ можно вычислять также по понижению температуры замерзания, по повышению температуры кипения, по осмотическому давлению и по др. свойствам растворов.

29. Кондуктометрическое измерение константы диссоциации, степени диссоциации, точки эквивалентности при титровании.

К ондуктометрия – измерение электрической проводимости электролитов. Для измерения сопротивления электролитов применяется мостовая схема Уитстона:

2 – генератор переменного тока (постоянный вызывает электролиз р-ра)

R_x – измерительная ячейка;

R_M – магазин сопротивлений (известно)

в – положение передвижного контакта (подбирается так, чтобы нуль-инструмент 1 не показывал ток или показывал min, тогда

R_x = R_M (R₁/R₂) = R_M (ав/вб)

Действительная электрическая проводимость р-ра определяется концентрацией раствора, природой компонентов и температурой. Истинная электрическая проводимость р-ра  пропорциональна экспериментально измеренной величине ’: =k’, где k – константа сосуда – хар-ка ячейки – зависит от площади электродов, расстояния м/у ними, формы сосуда, объема р-ра, проводящего ток, находят экспериментально  станд-ых р-ров, чаще всего КCl.

По экспериментальным данным рассчитываются значения удельной:

и эквивалентной электропроводности:

Для расчета степени диссоциации слабого электролита используется уравнение:

, где λ^∞=^_к+_А^ - определяется по подвижностям ионов

Константу диссоциации бинарного электролита

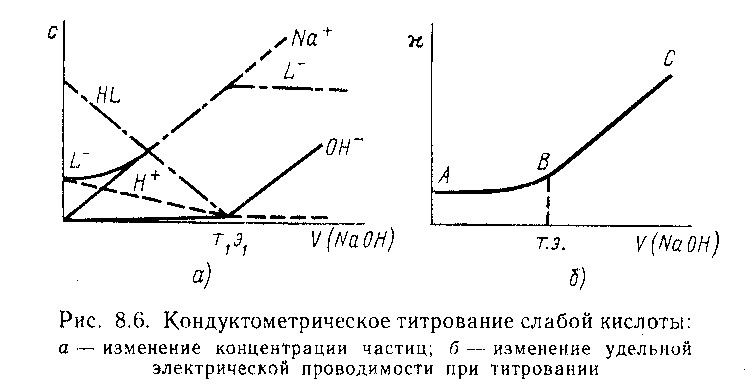
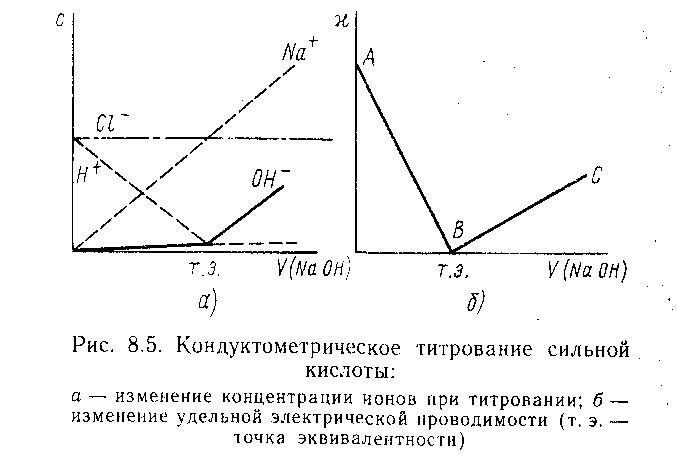
При кондуктометрическом титровании строится кривая зависимости электропроводности титруемого раствора от количества прибавленного титр. агента. Точка эквивалентности определяется по излому кривой этой зависимости. Резкое изменение электрической проводимости происходит, когда в процессе титрования образуются (или исчезают) малодиссоциирующие или труднорастворимые соединения.

Кислотно-основное титрование:

Изменение электрической проводимости до точки эквивалентности будут определяться действием 2-х взаимно противоположных тенденций:  за счет  с_Н+, имеющего подвижность 350 Смсм²/(моль-экв), что намного превышает подвижность иона Na⁺

[50 Смсм²/ (мольэкв)]

После точки эквивалентности начинается резкий электрической проводимости (ветвь ВС), т.к. в растворе будет нарастать концентрация ионов Na⁺ и ОН^-, подвижность кот. составляет 199 Смсм²/ (мольэкв)

30. Причина появления электродных потенциалов.

Электрохимическая цепь представляет собой систему, состоящую из различных фаз, через границы раздела которых переходят заряженные частицы, что вызвано стремлением системы к термодинамическому равновесию. При этом на границах раздела фаз возникают скачки потенциала.

Состояние заряженной частицы в фазе определяется электрохимическим потенциалом μ_Э, который согласно Гугенгейму представляет собой сумму ее химического потенциала μ и электрической энергии:

, где z – заряд частицы, F – число Фарадея, g – внутренний потенциал, отвечающий работе переноса элементарной отрицательно заряженной частицы из бесконечности в вакууме в глубь фазы. Переход незаряженных частиц из одной фазы в другую обусловлен неравенством химических потенциалов частиц в этих фазах. При этом работа переноса 1 моль вещества соответствует разности электрохим. потенциалов μ₁ и μ₂. Если через границу раздела фаз переносятся заряженные частицы, то кроме работы на преодоление сил химического взаимодействия необходимо произвести дополнительную работу против электрических сил. Мерой работы будет служить разность электрохимических потенциалов:

(при равновесии)

Переход заряженных частиц через границу раздела фаз сопровождается нарушением баланса электрических зарядов в каждой фазе и приводит к возникновению двойного электрического слоя, которому соответствует скачок потенциала.

Согласно сольватационной теории электродного потенциала, возникновение скачка потенциала на границе раствор – металл обусловлено: 1) диссоциацией атомов металла на ионы и электроны внутри металла; 2)сольватацией ионов металла, находящихся на поверхности металла, при соприкосновении его с раствором, содер-щим молекулы раст-ля.

Скачки потенциала между фазами не поддаются экспериментальному определению. Поскольку ЭДС электрохимической системы может быть легко измерена, то принято электродный потенциал считать равным ЭДС цепи, составленной из водородного(слева) и данного электрода(справа).

31. Термодинамический вывод уравнения для определения электродного потенциала.

Для обратимой реакции:

ν₁А₁+ ν₂А₂= ν₃А₃+ ν₄А₄

протекающей при постоянных давлениях и температуре в электрохимической цепи, уменьшение энергии Гиббса равно максимально полезной работе. Последняя, в свою очередь, соответствует электрической работе zFE электрохимической цепи, ЭДС которой равна Е. Следовательно:

, где z-число электронов, участвующих в электродных реакциях; F-пост-ая Фарадея. Максимально полезная работа выражается уравнением:

и соответствует электрической работе при ЭДС цепи Е, равной zFg:

(где z – количество электронов, участвующих в электродных реакциях)

Если активность каждого участвующего в реакции вещества равна 1, то ЭДС цепи называется стандартной:

Тогда:

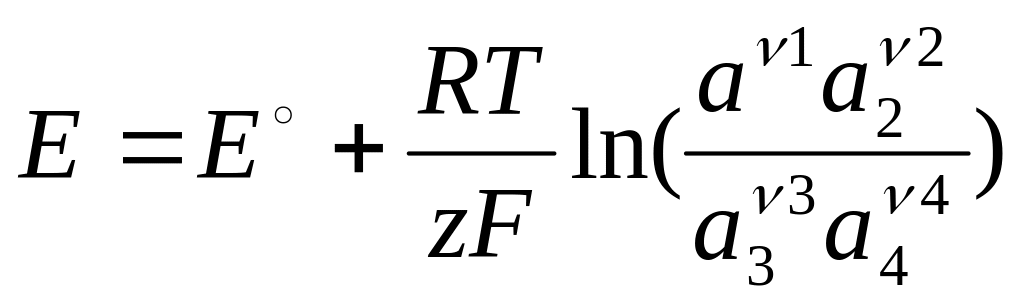
Обозначив 2,3RT/F = b_o (при 298 К

b_o = 0,059) получаем:

Из уравнения изотермы химической реакции: -ΔG^o = RTlnK_a=zFE^o

(где K_a – константа равновесия) получаем:

Для расчета значений электродных потенциалов, выраженных в условной водородной шкале, эти уравнения принимают вид:

,

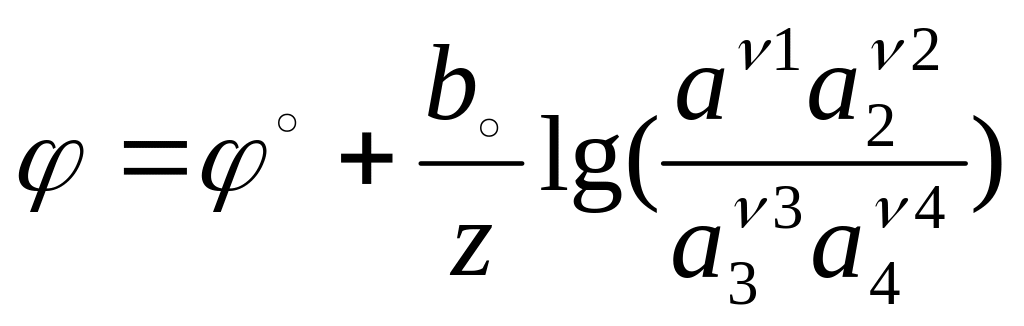и

32 Виды гэ

Виды гальванических элементов.

Различают химические и концентрационные гальванические элементы. В химических электроды отличаются друг от друга химическими св-ми. В этих элементах источником тока служит химическая реакция. Различают химические элементы с 2 и 1 электролитом. К ГЭ с 2-мя электролитами относится элемент Даниэля-Якоби.

Химические цепи 2-х видов.

1) цепях первого на одном электроде протекает реакция с участием катиона электролита (электрод I рода), а на другом электроде – с участием аниона электролита (электрод II рода)

(-)Zn /ZnCI_2(aq) / Hg₂CI₂, Hg(+)

На положительном и отрицательном электродах протекают реакции:

(+)Hg₂CI_2(т) +2 e↔ 2Hg_(T) + 2CI ^–

( - ) Zn²⁺ +2e↔ Zn _(T)

Суммарная Hg₂CI_2(т) - Zn²⁺ ↔ 2Hg_(Ж) + 2CI ^– - Zn_(T)

Получаем выражение для электродных потенциалов

Слева пишем окисленную форму и принятые электроны, а справа восстановленную форму.

ЭДС химической цепи определяется как разность потенциалов правого(положительного) и левого (отрицательного) электродов или уравнению:

2) Элементы второго вида с одним электролитом на обоих электродах протекают реакции с участием одного и того же аниона электролита; при этом, например, один электрод – газовый, и другой второго рода(сравнения).

(-)Hg, Hg₂Cl₂| KCI(aq)| CI₂, Pt (+)

Реакции на электродах

(+) СI₂+2e↔2CI^-

(-)Hg₂Cl_2(T) + 2e↔ 2CI^- +2Hg_(T)

Суммарная реакция в элементе

2Hg_(T)+ Cl_2(Г)↔Hg₂CI_2(T)

Хим. Цепи с одним электролитом широко применяется в физико-химических исследованиях из-за отсутствия в них диффузионного потенциала на границе двух растворов электролитов.

Концентрационные элементы, концентрационные цепи, один из видов гальванических элементов. Это цепи, в кот. Оба электрода одинаковы по своей природе, но различаются активностью одного или нескольких участников электродной реакции. При этом электрическая энергия получается за счет выравнивания концентраций веществ в элементе.

Различают К. э. двух типов:

1) без переносом ионов называются элементы:

а)с одинаковыми электродами и 2-мя одинаковыми по природе, но разными по концентрации растворами электролитов, причем м/д растворами отсутствует непосредственное соприкосновение;

б)с электродами из 2х сплавов (амальгам), одинаковых по природе, но разных по концентрации(с одним раствором электролита);

в)с газовыми электродами, одинаковыми по природе, но с разным давлением газа на электродах( с одним раствором электролита)

2) с переноса ионов.К. э. с переносом ионов получают погружением двух одинаковых электродов (например, серебряных) в разделённые полупроницаемой перегородкой растворы одного и того же электролита (например, нитрата серебра) различной концентрации. Электродвижущая сила в таких К. э. возникает в результате непосредственного переноса электролита из более концентрированного раствора в менее концентрированный. В К. э. второго типа выравнивание концентраций электролита происходит в результате химических процессов, происходящих на двух различных электродах.

К электрохимическим элементам относится элемент Даниэля-Якоби:

33 Вычисление эдс обратимого гэ, химического или концентрационного

В электрохимических системах происходит взаимное превращение энергии химических реакций в электрическую энергию и обратно. Применение законов термодинамики к электрохимическим системам позволяет рассчитать значения равновесных электродных потенциалов и э. д. с. электрохимических цепей. Для обратимой реакции протекающей при постоянных давлении и температуре в электрохимической цепи, максимальная полезная работа выражается уравнением , где Е- эдс элемента

и соответствует электрической работе при э. д. с. цепи Е, равной zFЕ. Отсюда 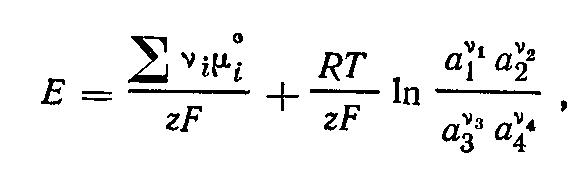где z— количество электронов, участвующих в электродных реакциях (одинаковое для обоих электродов); F — число Фарадея. Если активность каждого участвующего в реакции вещества равна 1, то э. д. с. цепи называется стандартной и равна

В соответствии с этим уравнение принимает вид

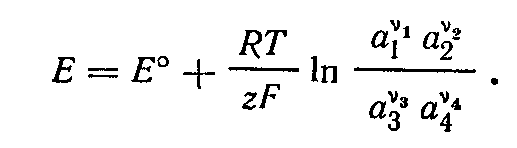Обозначив получаем

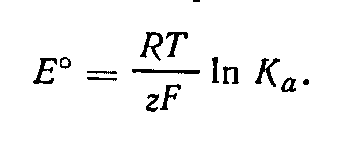Из уравнения изотермы химической реакции следует где Ка — константа равновесия реакции (Ка = К°). Отсюда Связь между э. д. с. электрохимической цепи и изменением энтальпии протекающей в ней реакции устанавливается на основании уравнения Гельмгольца — Гиббса

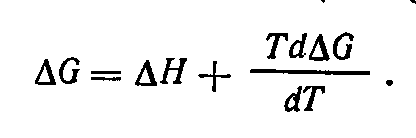
34 Диффузионный потенциал электрохимические цепи могут содержать несколько электролитов, границам раздела которых соответствуют гальвани-потенциалы, называемые фазовыми жидкостными потенциалами. Для двух растворов с одинаковым растворителем такой потенциал называется диффузионным. В месте контакта двух растворов электролита КА, отличающихся друг от друга концентрацией, происходит диффузия ионов из раствора 1, более концентрированного, в раствор 2, более разбавленный. Обычно скорости диффузии катионов и анионов различны. Допустим, что скорость диффузии катионов больше скорости диффузии анионов. За некоторый промежуток времени из первого раствора во второй перейдет больше катионов, чем анионов. В результате этого раствор 2 получит избыток положительных зарядов, а раствор 1 — отрицательных. Поскольку растворы приобретают электрические заряды, то скорость диффузии катионов уменьшается, анионов увеличивается, и с течением времени эти скорости становятся одинаковыми. В стационарном состоянии электролит диффундирует как единое целое. При этом каждый раствор имеет заряд, и разность потенциалов, установившаяся между растворами, соответствует диффузионному потенциалу. Расчет диффузионного потенциала в общем случае затруднителен. С учетом некоторых допущений Планком и Гендерсоном выведены формулы для расчета. Так, например, при контакте двух растворов одного и того же электролита с различной активностью ( )

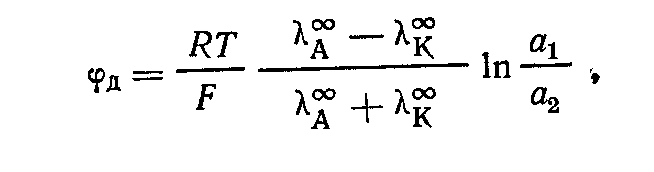
где — предельные подвижности ионов. Э. д. с. электрохимической цепи с учетом диффузионного потенциала будет

Поскольку расчет и экспериментальное определение диффузионного потенциала затруднены, то при измерениях э. д. с. исключают, используя соленой мостик. Последний представляет собой концентрированный раствор электролита , подвижности ионов которого приблизитеьяо одинаковы (КСl, КNОз). Соленой мостик, например КСl, располагают между растворами цепи, и вместо одной жидкостной границы в системе имеются две.

35.Определение термодинамических характеристик обратимого гальванического элемента. В электрохимических системах происходит взаимное превращение энергии химических реакций в электрическую энергию и обратно. Применение законов термодинамики к электрохимическим системам позволяет рассчитать значения равновесных электродных потенциалов и э. д. с. электрохимических цепей. Для обратимой реакции протекающей при постоянных давлении и температуре в электрохимической цепи, максимальная полезная работа выражается уравнением и соответствует электрической работе при э. д. с. цепи Е, равной zFЕ. Отсюда где z— количество электронов, участвующих в электродных реакциях (одинаковое для обоих электродов);

F — число Фарадея. Если активность каждого участвующего в реакции вещества равна 1, то э. д. с. цепи называется стандартной и равна

В соответствии с этим уравнение принимает вид

Обозначив получаем

Из уравнения изотермьг химической реакции следует где Ка — константа равновесия реакции (Ка = К°). Отсюда Связь между э. д. с. электрохимической цепи и изменением энтальпии протекающей в ней реакции устанавливается на основании уравнения Гельмгольца — Гиббса Убыль энергии Гиббса соответствует максимальной полезной (электрической) работе цепи:

Из определения энергии Гиббса следует Сравнивая уравнения получаем Из уравнения видно, что электрическая работа цепи в общем случае не соответствует тепловому эффекту реакции. Если , то электрическая работа меньше энергии химического процесса, электрохимическая система отдает теплоту в окружающую среду или нагревается в условиях тепловой изоляции. При электрическая работа системы больше энергии химической реакции; недостаток энергии система заимствует из окружающей среды или охлаждается в условиях тепловой изоляции.

36(1).Электроды 1 и 2 рода, окислительно-восстановительный, сравнения. Электроды первого рода. В потенциалопределяющих реакциях на этих электродах участвует один вид ионов. Металлические электроды, обратимые относительно катионов (в том числе и амальгамные), и металлоидные, обратимые относительно анионов: Уравнение потенциалопределяющей реакции на электродах, обратимых относительно катионов, Электродный потенциал с учетом того, что активность твердого вещества при данной температуре постоянна и равна единице: А м а л ь г а м н ы е электроды состоят из амальгамы металла, находящейся в контакте с раствором, содержащим ионы этого металла : Уравнения потенциалопределяющей реакции электрода и его потенциала: 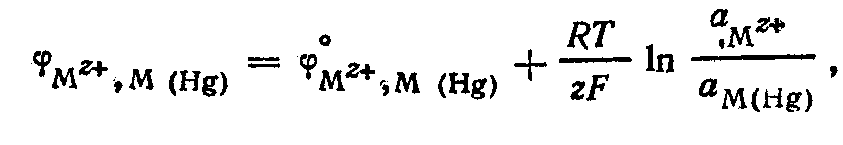К электродам первого рода относятся также газовые.

Водородный электрод пластинка из платины, покрытая электролитической платиновой чернью, погруженной в раствор, содержащий потенциалопределяющие вещества, через который пропускается водород. В кислой среде системе отвечает уравнение потенциалопределяющей реакции которое может быть записано в упрощенном виде:

Потенциал водородного электрода

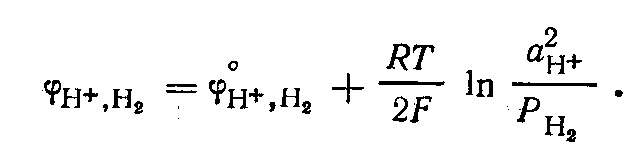
Поскольку стандартный потенциал водородного электрода при всех температурах условно принят равным нулю, то при Р, = 1 потенциал электрода определяется рН раствора: В щелочной среде в системе протекает потенциалопределяющая реакция по уравнению которому отвечает уравнение для расчета потенциала: Водородный электрод применяется как индикаторный при экспериментальном определении рН растворов. Кислородный электрод по устройству аналогичен водородному электроду. В щелочной среде для системы электродный процесс и отвечающее ему уравнение для расчета потенциала

Создать практически кислородный электрод с данной реакцией не удается, так как в реальных условиях металлы под действием кислорода окисляютсяэПотенциал Кислородного электрода как в щелочной, так и кислой среде зависит от рН раствора:

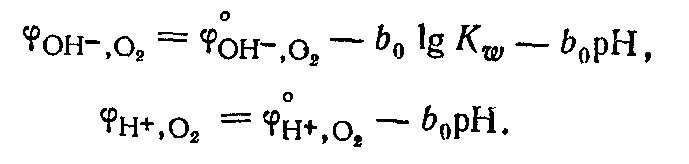
Электроды второго рода.

Т акие электроды состоят из трех фаз: металл покрыт слоем его труднорастворимой соли и погружен в раствор, содержащий анионы, одноименные с анионами соли:

В потенциалопределяющей реакции на этом электроде принимают участие как катионы, так и анионы. Электрохимическому процессу сопутствует химическая реакция, приводящая к осаждению или растворению МА: Суммарное уравнение реакции, согласно которой электрод обратим относительно аниона, Последней реакции соответствует уравнение для расчета электродного потенциала

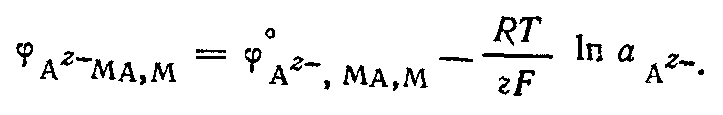
Электрод второго рода можно рассматривать как электрод первого рода, обратимый относительно катиона у которого активтность в растворе определяется растворимостью МА. Вследствие устойчивости потенциалов электроды второго рода могут быть использованы как электроды сравнения при потенциометрических измерениях. для этого наиболее употребительны каломельный и хлорсеребряный электроды. Каломельный электрод состоит из ртути, покрытой пастой, содержащей каломель, и соприкасающейся с раствором хлорида калия: .

Уравнение потенциалопределяющей реакции По концентрации применяемого раствора КСI различают 0,1 н., 1 н. и насыщенный каломельные электроды. Последний имеет наиболее широкое применение.

Хлорсеребряный электрод серебряная пластинка, покрытая АgС1 и погруженная в раствор КСI. Уравнение электродной реакции Окислительно-восстановительные электроды. Все электроды, которым соответствует потенциалопределяющие реакции с участием электронов, представляют собой окислительно-восстановительные системы. Однако принято в особую группу выделять электроды, в потенциалопределяющих реакциях которых не участвуют простые вещества — газы, металлы. Эти электроды называются окислительновосстановительяыми (редокси-электроды). В общем виде схема электрода и уравнение потенциалопределяющей реакции записываются так: Сюда относятся в первую очередь электроды, у которых Ох и Red представляют собой ионы, причем электродная реакция состоит в перемене их заряда. Потенциал окислительно-восстановительного электрода для систем, характеризующихся равновесием , потенциал рассчитывается по уравнению Кроме относительно простых окислительно-восстановительных электродов существуют более сложные, в потенциал- определяющих реакциях которых участвуют ионы Н+ и молекулы воды. Например, системе отвечают уравнения электродной реакции и для расчета потенциала электрода:

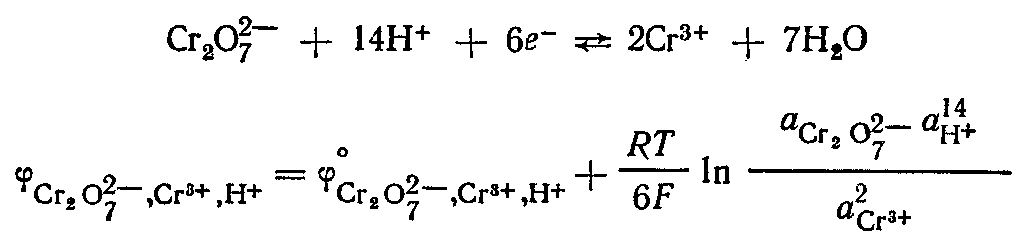
Из расчетного уравнения видно, что потенциал редокс электрода зависит от активности ионов Н+ в растворе. При условиях, обеспечивающих постоянство активностей других компонентов потенциалопределяющей реакции, такие окислительно-восстановятельньие электроды могут быть использованы как индикаторные при потенциометрическом определении рН растворов (например, хингидронный электрод). Стеклянный электрод представляет собой тонкую мембрану из специального стекла, в котором повышено содержание щелочных составляющих соединений натрия, лития и др.Согласно теории Б. П. Никольского потенциалопределяющий процесс на границе раствор — стекло заключается в обмене между ионами щелочного металла, например Na+, содержащимися в cтекле, и ионами Н+, находящимися в растворе.

37. Электрохимические методы определения рН растворов.

1) при помощи водородного электрода

Водородный электрод – Н+ | Н₂ , Pt – платиновая пластинка, погруженная в испытуемый р-р и омываемая струей водорода

Состояние равновесия H+ + e ↔ ½ H₂

Составляют электрохимический элемент

(-) H₂, Pt | H+ , A- || KCl | Hg₂Cl₂, Hg (+)

ЭДС этой цепи равна E = E_кал – E_{H+ | H2}

где E_кал - потенциал каломельного электрода

E_{H+ | H2}= -2,303b₀pH

“+” простота аппаратуры,

можно определять рН в р-рах, в кот.присутствуют окислители или восстановители,

отсутствие необходимости калибровки прибора

“-” длительность измерения,

получение газообразного водорода,

электрод из платинированной платины легко «отравляется» примесями,

область измерения в интервале рН от 1 до 8

2) с использованием хингидронного электрода

E⁰_xr – стандартный потенциал хингидронного электрода

“+” простота аппаратуры,

отсутствие необходимости калибровки прибора

“-” область измерения в интервале рН от 1 до 8,

нельзя определять рН в р-рах, в кот.присутствуют окислители или восстановители

3) при помощи стеклянного электрода

Сосуд из тонкого стекла с повышенной электрической проводимостью, наполненный р-ром, в кот.погружен электрод 1-го или 2-го рода.

E_ст = E⁰_ст -2,303b₀pH

где E⁰_ст - потенциал стеклянного электрода

Составляют электрохимический элемент

(-) Hg, Hg₂Cl₂ | KCl aq || испытуемый р-р, Н+ | стеклянный электрод (+)

ЭДС этой цепи равна E = E_ст – E_кал

38. Потенциометрическое титрование.

1) определение т/д характеристик хим.реакций

Измеряют э.д.с. цепи при различной температуре и определяют температурный коэф-т э.д.с. По этим данным рассчитывают изменение энергии Гиббса, энтальпии и энтропии.

2) определение средних ионных коэф-тов активности р-ров электролитов

Измеряют э.д.с. электрохимической цепи с одним электролитом (отсутствует диффузионный потенциал), электроды которой обратимы относительно катиона и аниона электролита.

3) определение стандартных потенциалов и констант равновесия электродных реакций

Измерив потенциал исследуемого электрода φ, можно рассчитать его стандартный потенциал φ⁰.

39. Определение понятий:

ν₁А₁+ν₂А₂+…+ν_nА_n→ν’₁A’₁+ν’₂A’₂+…+ν’_nA’_n,

где ν_i и ν’_i – стехиометрич. коэф. исходных и полученных вещ-в

А_i и А’_i- исходные и полученные вещ-ва.

υ=kcⁿ¹_A1cⁿ²_A2…cⁿⁿ_An

c – концентрации реагирующих вещ-в

Скорость реакции (υ) – кол-во молекул данного сорта, реагирующих в единицу времени.

Константа скорости реакции (k) – скорость реакции при условии, что концентрации реагирующих вещ-в равны 1. c_A1=c_A2=…=c_An=1, υ=k

Порядок реакции по данному вещ-ву – число, равное степени n_i , в которой концентрация этого вещ-ва входит в кинетическое ур-ние реакции. Сумма степеней n₁+n₂+…+n_n – порядок реакции в целом. Целое /дробное,

положит./ отрицат.

Молекулярность – число молекул, участвующих в элементарном хим. акте (акт взаимодействия частиц, в рез-те кот. образуются новые частицы продуктов рекции или промежуточных соединений) всегда целое положит.

k=Ce^-E/RT

Энергия активации (E) – тот избыток энергии по сравнению со средней энергии молекул при данной температуре, которой должны обладать молекулы, чтобы они могли вступить в хим. реакцию. Если E↑, то υ↓

Предэкпоненциальный множитель (C) – константа, характеризующая реакцию.

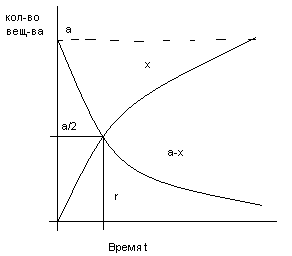
Время полураспада (τ): время, соответств. точке пересечения кривых.

х – прореагировавшее кол-во, а-х – оставшееся кол-во.

х=а/2 к моменту времени τ прореагирует половина исх. вещ-ва

40. Вывод уравнения кинетики односторонней реакции 1 и 2 порядка.

1) А→В

- концентрация в-ва А в момент времени t, V объём системы

если t=0, x=0, то

, c₀ - исходная концентрация, с - концентрация к моменту времени t

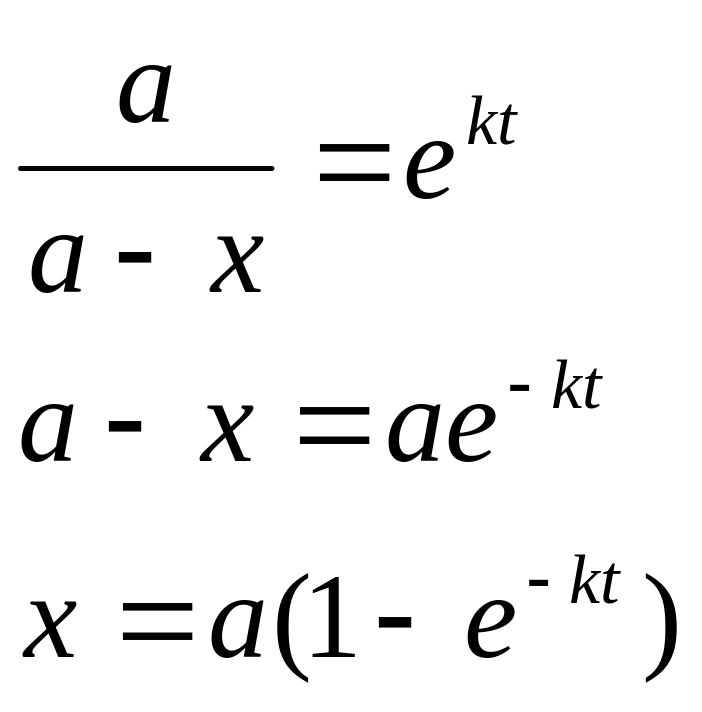
время полураспада х=а-х

время полураспада не зависит от количества исходного вещ-ва

2) А+В→С+D+…

если V=const, то

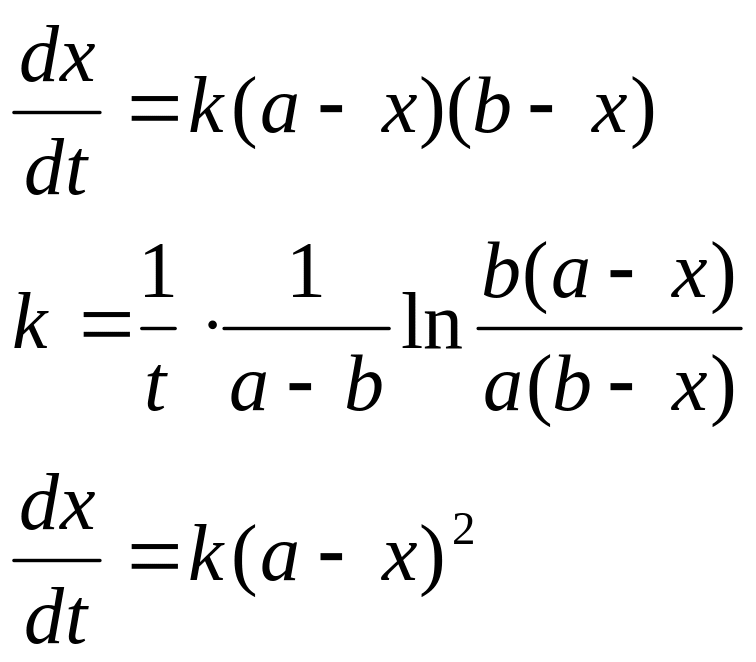если a=b, то

время полураспада обратно пропорционально кол-ву исх.вещ-ва

41. Вывод уравнения кинетики двусторонней реакции 1 порядка.

A k₁↔k₂ B

Принцип независимости: если в системе одновременно протекает несколько реакций, то каждая из них независима от остальных и скорость её прямо пропорциональна концентрации реагирующих веществ.

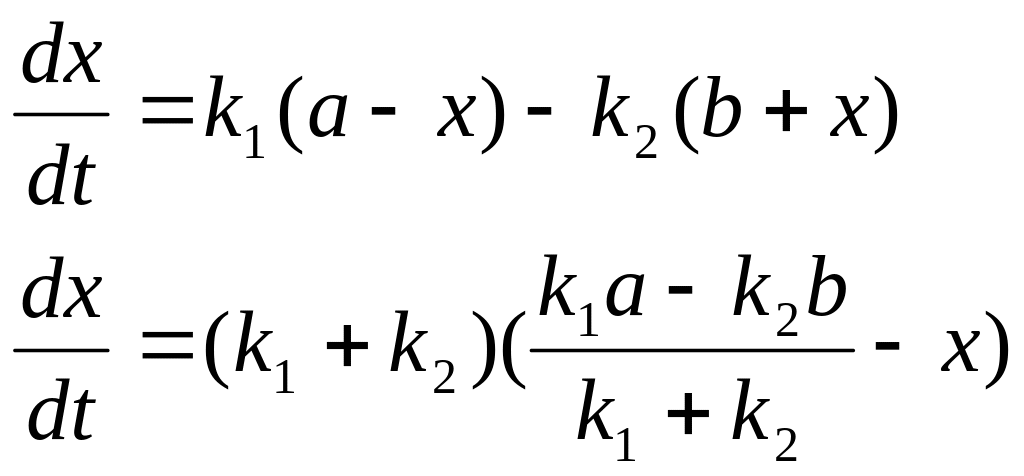
Пусть

тогда

где К – константа равновесия

в момент равновесия тогда

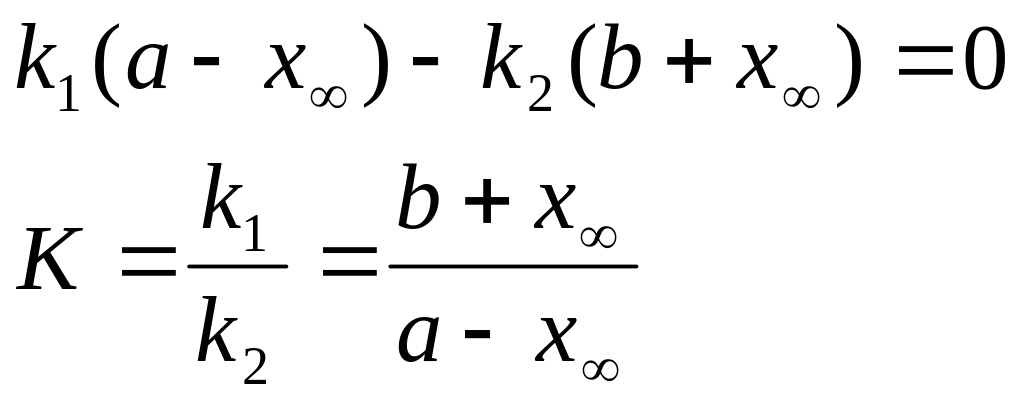
где х_∞ - кол-во вещ-ва А, прореагировавшего к моменту равновесия

Если считать как необратимую , то

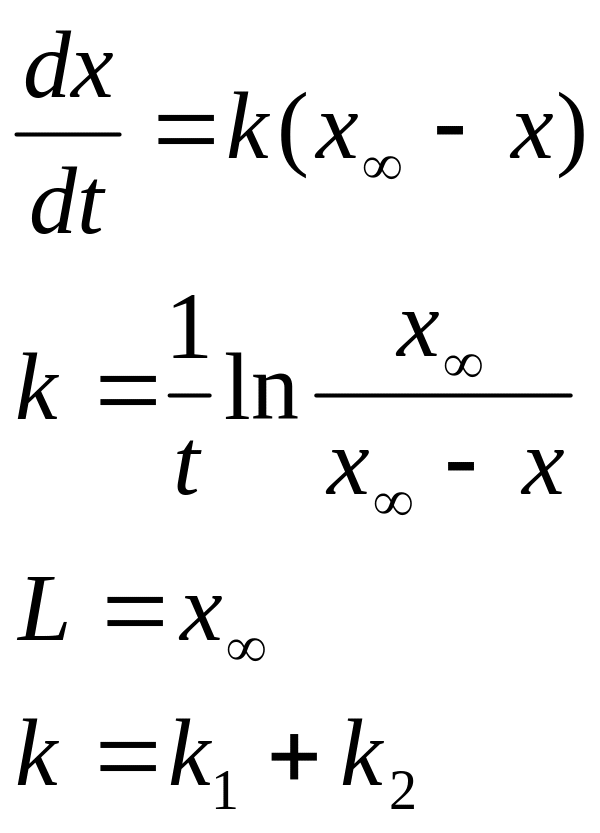
42. Вывод уравнения кинетики параллельных односторонних реакций

1 Порядка.

Если исходные вещ-ва реагируют одновременно в нескольких направлениях, то такие реакции наз. параллельными.

А→B скорость реакции

А→С скорость реакции

43. Кинетические кривые и уравнения скорости последовательной реакции.

Это реакции с промежуточными стадиями

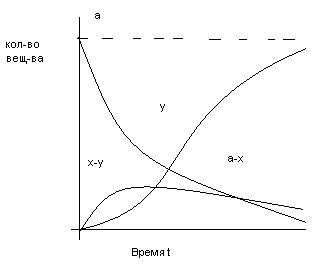
Кривая (x-y) изменения количества промежуточного вещ-ва имеет максимум t_max , при котором наиб. кол-во прмежуточ. вещ-ва

Пусть тогда

Чем больше k2/k1, тем больше ордината максимума (x-y)

y=f(t) характеризует накопление продукта: точка перегиба(т.е. вещ-во образуется с начальным ускорением) совпадает с точкой максимума (x-y)

44. Методы определения порядков реакции.

1) порядок реакции в целом = сумме порядков реакции по каждому вещ-ву

Порядок реакции по данному вещ-ву: изменение концентрации только данного вещ-ва, для этого концентрации остальных вещ-в должны быть велики, чтобы изменением их можно было пренебречь.

ν₁А+ν₂B+ν₃C→ν₄D+ν₅E,

, где k₁=kc_Bⁿ²c_Cⁿ³,

n_i – степень, в кот. концентрация i-го вещ-ва входит в ур-ние реакции

2) по времени полураспада: задавать каждый раз исходную концентрацию данного вещ-ва (несколько опытов). Выяснить зависимость вр.полураспада от кол-ва исх.вещ-ва

n= n₁+n₁+…+n_i – суммарный порядок реакции

r~ , где a – концентрация исх.вещ-ва

3) все вещ-ва, кроме А, берутся в избытке; задают 2 различных начальных значения концентрации:

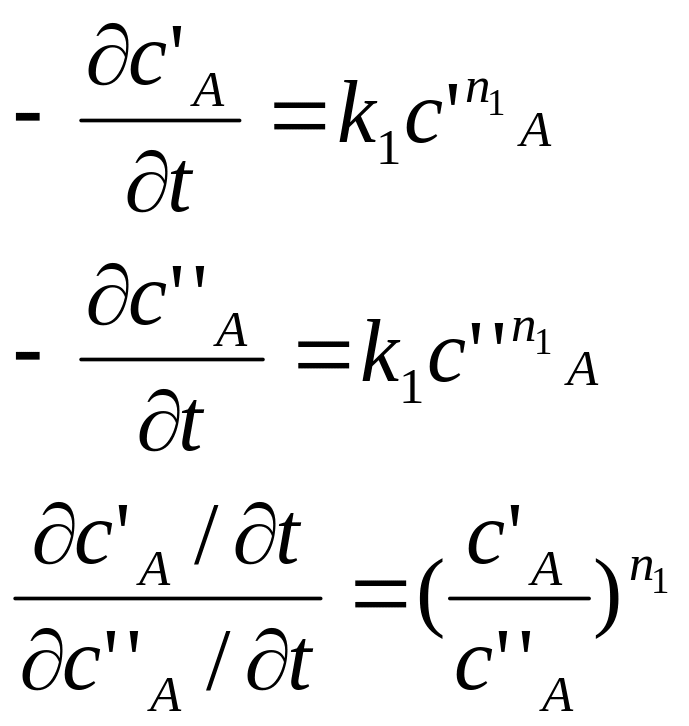
порядок реакции по вещ-ву А

4) графический:

t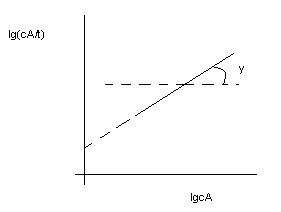 gφ= порядку реакции по данному вещ-ву

- средняя скорость реакции

С_А – концентрация вещ-ва А в каждый момент времени

5) метод подбора: проверяют, какое из ур-ний лучше описывает опытные данные. Ур-ние описывает процесс, если полученные по нему значения констант колеблются около какой-то средней величины.

45. Методы определения энергии активации.

Энергия активации (E) – тот избыток энергии по сравнению со средней энергии молекул при данной температуре, которой должны обладать молекулы, чтобы они могли вступить в хим. реакцию. Если E↑, то υ↓

ур-ние Аррениуса

1. графический:

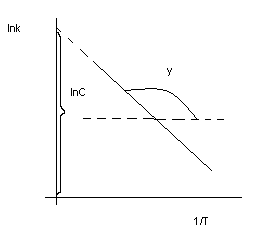
lnC – константа интегрирования

Отсюда определяем величину энергии активации.

2. по энергетическому барьеру:

и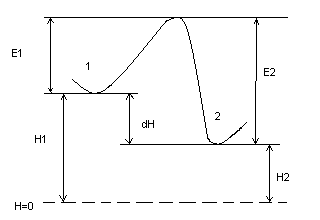 з состояния 1 в состояние 2 при затрате энергии Е₁, обратный переход при затрате энергии Е₂

∆Н = Е₂ - Е₁

-∆Н = Н₁ - Н₂

46. Зависимость константы скорости реакции от температуры.

С увелич-м температуры, скорость хим. р-ции обычно возрастает. В областях умеренных температур можно воспользоваться правилом Вант-Гоффа: при увеличении Т на 10ºС скорость реакции возрастает в 2-4 раза.

Наиболее широко применимое уравнение Аррениуса:

Проинтегрировав Е_а от Т получим: k=A (1), где А-постоянная интегрирования- предэкспоненциальный множитель.

Определив константы скоростей при нескольких температурах, по (1) можно рассчитать А и Е_а 2,3 lg , откуда Е_а= Определив Е_а по (1) найдем А.

Уравнение (1) может быть записано и в линейной форме:

47. Вычисление константы скорости бимолекулярной реакции по числу соударений.

А+В С

К – константа скорости.

Для молекул разного сорта общее число бимолекулярных столкновений определяется по уравнению:

, где

r_AB – диаметр, равный сумме двух радиусов r_A и r_В молекул А и В

n’_A, n’_B – число активных молекул газа в 1 см³

М_А, М_В – молекулярные массы А и В

Величина средней арифметической скорости w определяется по формуле

Число активных молекул А и В может быть рассчитано по закону Больцмана

Число активных столкновений в 1 см³ в единице времени будет равно

(5)

Суммарная энергия будет равна

Е = Е₁ + Е₂ (6)

Подставим (6) в (5)

Зная что

-(∂Ca/∂τ)_v = Z_AB/N_i

N_i = N_A/22400

N_i – число молекул в 1 см³

-число молекул в 22400 см³

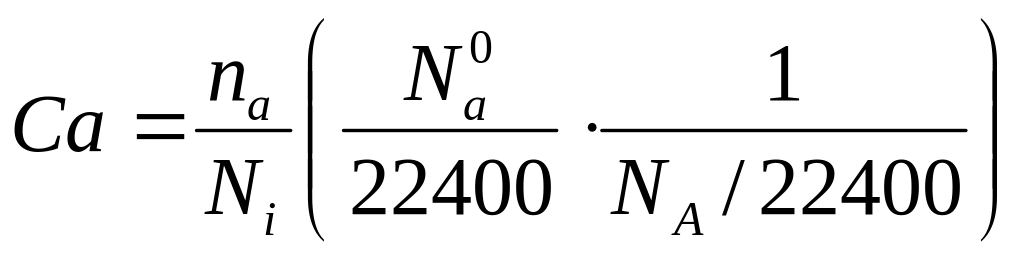
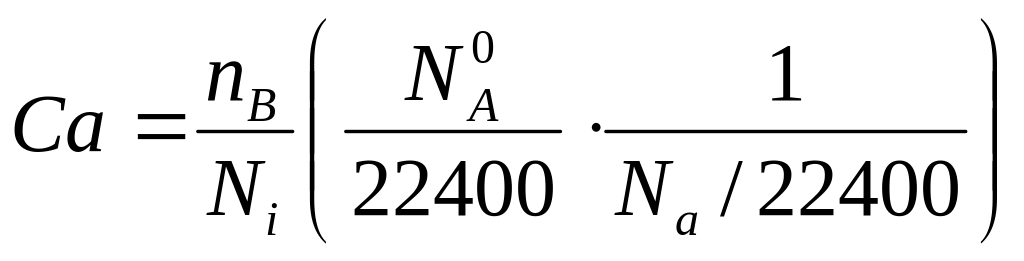
Согласно основному постулату кинетики

-(∂Ca/∂τ)_v = KCaC_B или -(∂Ca/∂τ)_v = K∙n_an_B/(N_i)² (*)

Подставим (*) в (8)

находим К: К = К₀e^-E/RT,

Где K₀=

48. Основные теории переходного состояния.

В модели активного комплекса предполагается, что исходная конфигурация реагирующих частиц, обладающих достаточной энергией для преодоления барьера реакции, преобразуется при непрерывном изменении межатомных расстояний и соответствующей энергии системы в активный комплекс, который обязательно превращается в продукты реакции:

АА + В → {ААВ}

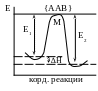Для превращения исходных молекул АА и В в продукты они должны образовать активный комплекс {ААВ}, в нем старые связи разрыхлены и наметились новые, но их конфигурация и энергия не соответствуют стабильным молекулам.

E₁ и Е₂ – энергия активации прямой и обратной реакций

∆Н = Е₁-Е – теплота реакции

Вначале АА и В поднимаются до точки М, которая представляет собой энергетический перевал, затем активный комплекс распадается и молекулы А и АВ «скатываются вниз» в потенциальную яму.

Активный комплекс находится в состоянии равновесия с исходными веществами, причем одна из колебательных степеней свободы вырождается в поступательную по координатам реакции и дальше активный комплекс необратимо превращается в продукты. Прямой и обратный процессы с образованием активного комплекса протекают независимо друг от друга.

Скорость реакции согласно теории будет равна числу активных комплексов, проходящих через потенциальный барьер вдоль координаты реакции в единицу времени, в еденице реакционного пространства.

49. Связь константы скорости реакции с энтальпией и энтропией активации.

AB + С A…B…C A + BC

Выражение константы скорости для бимолекулярной реакции:

(5), где χ – трансмиссионный коэффициент, определяет долю активных комплексов, прошедших через точку М.

Изменение энергии Гиббса для активных комплексов при стандартных условиях равно теплоте и энтропии активации или константе равновесия К_р^#.

; => (6)

Подставив (5) в (6):

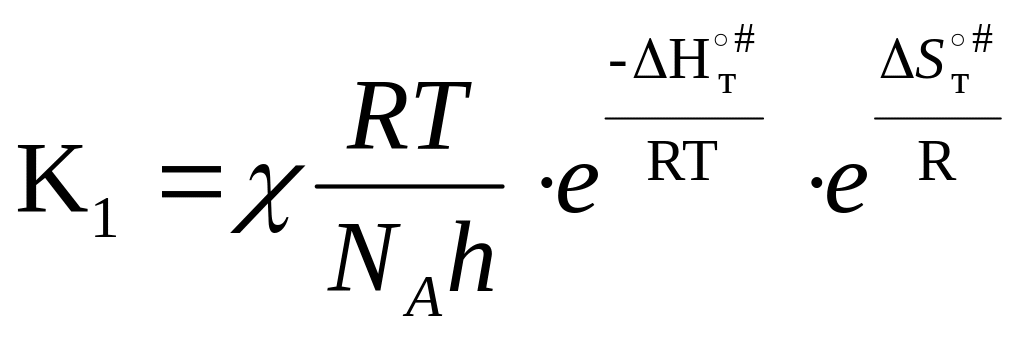(7)

Используя уравнение Аррениуса: K₁ = K₀₁exp(-E/RT) и (7) можно найти связь между теплотой активации и энергией активации и выражение для K₀₁:

Логарифмируем (7):

и дифференцируем по Т (∆S^0#=const)

; (8)

Сравнивая с уравнением Аррениуса:

=> ; (9)

Подставляя (9) в (7):

=>

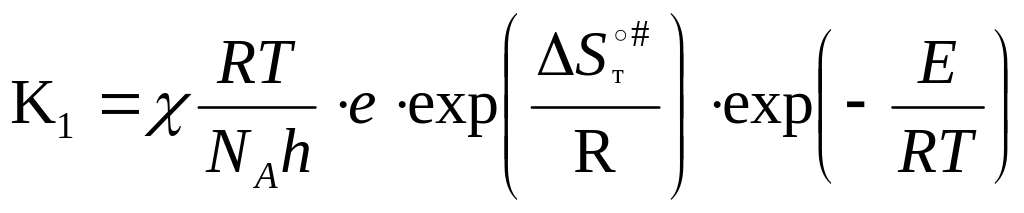По величине реакции делят на «нормальные» ( =0, exp( /R)=1), «быстрые» ( >>0, exp( /R)>>1) и «медленные» ( <<0, exp( /R)<<1).

exp( /R) приобретает смысл стерического множителя.

50. Основные законы Фотохимии. Кинетика фотохимической реакции.

Фотохимические реакции-это реакции кот. Проходят под действием на молекулы реагирующих веществ ультрафиолетового света.

Закон Гротгуса: химически активны лишь те лучи, кот. поглащаются реакционной смесью.

Закон Ламберта-Бера: ослабление интенсивности dI света прошедшего через слой толщиной dl, прямо пропорционально толщине слоя и интенсивности падающего света I:

, где k-множитель пропорц-ти, называемый молекулярным коэффициентом поглащения; n- число поглативших свет молекул в 1см³.

Количество энергии Q, поглащаемой в единицу времени t:

Тогда согласно закону Вант-Гоффа скорость фотохимической реакции пропорциональна количеству энергии, поглащенной веществом в единицу времени t: = , где K- множитель пропорциональности.

Закон Штарка-Эйнштейна: каждому поглащенному кванту излучения hν cоответ-т одна измененная молекула: число молекул-

Во многих случаях число фотохимически прореагир-х молекул не равно числу поглащенных квантов. Вводим понятие квантового выхода γ- отношение числа прореагир-х мол-л к числу поглащенных квантов: γ= ,тогда выражение скорости:

Кинетика:

HI+hν H+I первичный процесс

H+HI H₂+I

I+I+M I₂+M вторичные процессы

Уравнения кинетики для этой схемы запишутся в таком виде:

(1)

(2)

(3)

На основе принципа стационарности Боденштейна и

Из 2 и 3 получим: и и подставив в 1, имеем:

или (4)

Откуда получим квантовый выход для реакции разложения HI:

Из уравнения 4 следует, что скорость реакции разложения HI прямо пропорциональна интенсивности поглащенного света и количеству молекул HI, поглотивших энергию излучения.

51.Квантовый выход. Примеры реакций с различным квантовым выходом.

Для определения эффективности действия излучения на вещество вводится понятие квантового выхода. Квантовый выход определяется как отношение числа прореагировавших молекул к общему количеству поглащенных квантов лучистой энергии: γ= Следует отметить, что γ зависит от доли вторичных реакций , длины падающего света, а скорость фотохимической реакции зависит также и от температуры реакции, хотя и в не очень значительной мере.

Квантовый выход в практических случаях может иметь значение меньшее единицы. Примером таких реакций является разложение оксида азота 2NO = N₂+O₂ γ=0,75. Низкое значение кв-го выхода определяется дезактивацией первичных активных частиц при высвечивании энергии, гибели радикалов в тройных столкновениях на третьих частицах и другими причинами.

В реакции разложения гидропероксида водорода по схеме Н₂О₂→Н₂О + О γ=1. Часто γ бывает больше 1. Так, при синтезе озона 3О₂→2О₃ γ=3. В случае, когда γ>> 1, процесс является цепным. В первичном акте в этом случае образуется возбужденная молекула, которая распадается на активные частицы, участвующие затем последовательно во многих последовательно чередующихся стадиях гибели и регенерации. Например реакция образования фосгена СО+Cl→COCl₂ γ=10³.

52. Цепные реакции (примеры, основные признаки).

Имеется класс специфических реакций, протекающих в газовой (а также в жидкой фазах) через образование высокоэнергетических (Е больше Е_а) возбужденных частиц, радикалов, атомов и др. Далее эти активные частицы быстро взаимодействуют с исходными реагентами, с образованием продуктов и регенерацией активных частиц. Таким образом, в результате зарождения малого числа активных частиц превращается большое число молекул реагентов. Такой циклический процесс называется цепным, причем повторяющаяся группа реакций называется цепью.

В цепном процессе выделяют этапы:

1) Зарождение (инициирование) цепи с образованием активных частиц (АЧ).

2) Развитие (продолжение) цепи, характеризуемое длиной цепи, l_ц, которая представляет собой число молекул реагента, прореагировавших на одну активную частицу, образовавшуюся на этапе зарождения цепи.

3) Обрыв цепи в результате процессов дезактивации/гибели активных частиц, например, на стенке (при малых давлениях) или при тройных соударениях с молекулами реагентов или примесей. Здесь материал стенки или третья частица играют роль «приемника» избыточной энергии, выделяющейся при ассоциации атомов и/или радикалов. За счет передачи этой энергии возможна стабилизация образующихся молекул (Н₂ или С1₂). Кроме указанных реакций, обрыв цепи может происходить за счет взаимодействия активных частиц с добавками (ингибиторами), при котором образуются относительно стабильные радикалы (например, типа стерически затрудненных фенолов или аминов).

Основными признаками наличия цепного процесса являются:

• существенное увеличение скорости развитого процесса (r) по сравнению с начальной скоростью (r_i); отношение r/r_i равно средней длине l_ц.

• образование нескольких молекул продукта на 1 молекулу инициатора или на 1 квант инициирующего излучения,

• зависимость скорости реакции от материала стенки реактора и отношения поверхности к объему реакционного пространства,

• сильная зависимость скорости реакции от концентрации добавок ингибиторов.

Проиллюстрируем эти этапы на примере реакции Н₂ + С1₂= 2НС1:

k_i

1) С1₂ + hν  С1₂* 2С1^ (инициирование)

2а) С1^ + Н₂  2НС1 + H^

k_р

2б) H^ + С1₂  НС1 + Cl^ и т.д. (продолжение цепи)

k_{t +НМ}

3а) H^ + М  НМ  Н₂ + М

k_t

3б) 2С1^ + НС1  С1₂ + НС1* (обрыв цепи на стенке а) и в объеме б))

где М – материал стенки.

Различают неразветвленные и разветвленные цепные реакции. Процесс называется неразветвленным, когда на этапе продолжения цепи превращение одной активной частицы приводит к образованию одной новой АЧ. Если при этом образуется больше одной новой активной частицы, такой цепной процесс называется разветвленным.

Наиболее трудным этапом цепного процесса обычно является инициирование. Этому этапу соответствует индукционный период наблюдаемой кинетической кривой. Цепной процесс может быть инициирован соответствующим излучением или веществами-инициаторами, например, из класса пероксидов, диазосоединений и т.п. По мере увеличения концентрации активных частиц (в рассмотренном примере радикалов H^ и Cl^) скорость реакции существенно возрастает до стационарного значения (в случае неразветвленной цепи) или до выгорания/взрыва (в случае разветвленной цепи) реакционной смеси. На заключительном этапе реакции, когда процессы обрыва АЧ преобладают над инициированием цепи, скорость реакции убывает во времени (рис. 17).

53. Кинетика неразветвленных цепных реакций.

Рассмотрим кинетику реакций с неразветвленными цепями. Обозначим концентрацию активных частиц «n». Очевидно, что в случае неразветвленной цепной реакции изменения концентрация АЧ изменяется только за счет протекания реакций 1-инициирование и 3-обрыв цепи.

k_i

1) С1₂ + hν  С1₂* 2С1^ (инициирование)

2а) С1^ + Н₂  2НС1 + H^

k_р

2б) H^ + С1₂  НС1 + Cl^ и т.д. (продолжение цепи)

k_{t +НМ}

3а) H^ + М  НМ  Н₂ + М

k_t

3б) 2С1^ + НС1  С1₂ + НС1* (обрыв цепи на стенке а) и в объеме б))

где М – материал стенки.

Тогда можно выразить скорость изменения концентрации активных частиц (n), определяющую скорость реакции, как:

dn/dt = r_i – k_tn (4.1)

или если преобладает обрыв цепи в объеме (при повышенных давлениях)

dn/dt = r_i – k_tn² (4.2)

где r_i – скорость инициирования. Обычно для протекания реакции обрыва не требуется активация (Е_t ~ 0) и k_t >> k_i, поэтому достаточно быстро устанавливается стационарная концентрация активных частиц, определяемая из условия dn/dt = 0 в уравнении (4.1) или (4.2). (если что-то непонятно, см. 52 и 54 вопросы) =)

54. Принцип стационарности как метод для вывода кинетических уравнений цепных реакций.

На основе рассмотренной феноменологической картины можно описать в стационарном приближении кинетику неразветвленной цепной реакции. Проиллюстрируем это на примере цепной реакции разложения ацетальдегида с образованием метана и монооксида углерода в качестве основных продуктов (также образуется несколько процентов водорода и этана):

СН₃СНО  СН₄ + СО (4.R1)

для которой наблюдается полуторный порядок реакции по ацетальдегиду.

На основании экспериментальных данных можно предложить следующую схему протекания реакции (11):

k_i

1. СН₃СНО  СН₃^ + НС^=О (инициирование цепи, разрыв связи С-С)

k₂

2. СН₃^ + СН₃СНО  СН₄ + СН₃С^=О (продолжение цепи, отрыв атома Н от ацетальдегида)

k₃

3. СН₃С^=О  СО + СН₃^ (продолжение цепи, разрыв связи С-С)

k_t

4. 2 СН₃^ + M  С₂Н₆ (обрыв цепи)

Взаимодействием радикалов СН₃^ + СН₃С^=О и СН₃С^=О + СН₃С^=О пренебрегаем ввиду отсутствия в продуктах ацетона и диацетила. Далее запишем условия стационарности для обоих радикалов, участвующих в продолжении цепи (радикал НС^=О обладает низкой активностью):

d[CН₃^]/dt = k_iC_A - k₂C_A[CН₃^] + k₃[СН₃С^=О]- k_t[СН₃^]² = 0 (4.3)

d[СН₃С^=О]/dt = k₂C_A[CН₃^] - k₃[СН₃С^=О] = 0 (4.4)

Объединяя (4.3) и (4.4), получим k_iC_A = k_t[СН₃^]² , откуда

[СН₃^] = (k_iC_A/k_t)^0,5 (4.5)

Скорость реакции определим по образованию метана (стадия 2)

d[CН₄]/dt = k₂C_A[CН₃^] (4.6)

или с учетом (4.5) окончательно получим теоретическое кинетическое уравнение

d[CН₄]/dt = k₂(k_i/k_t)^0,5C_A^1,5, (4.7)

которое в совокупности со схемой правильно отражает наблюдаемые закономерности

55.Понятие о пределах воспламенения и взрыва.3 предела взрыва.

Разветвленные цепные р-ции(ц.р.) могут переходить во взрывной режим при определ-ных давлениях,тем-ре,составе реакцион. смеси и др. переменных. Экспер-но, на примере окис-я сероводорода кислородом,было установлено,что смесь может 3 раза переходить во взрывной режим,т.е. в смеси можно создать 3 значения давлений и тем-ры,при к-рых она взрывается.Эти дав-я и тем-ры наз-ют пределами самовоспламенения смеси(см.рис.)Э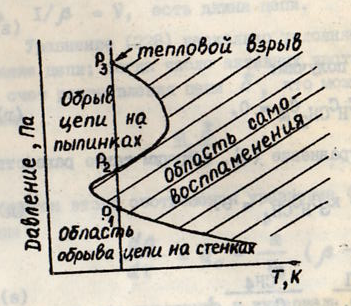 то объяс-ся след. образом.При дав-ях ниже Р₁ смесь H₂S и O₂ не взрыв-ся,т.к. она значит-но разбавлена(разрежена),и среднее число актов обрыва цепей на стенках сосуда, в к-ром нах-ся смесь, превышает число разветвлений цепей. Повышая,след-но,внешнюю поверх-ть сосуда или вводя в сосуд тв. зерна с развитой поверх-тью,можно изменять пределы дав-я и тем-ры для нижнего критич. предела взрыв-ти Р₁.При Р₁ смесь взрыв-ся,т.к. в этом случае число обрывов цепи уже ниже числа развития цепей.При дав-ях выше Р₂ смесь не взрыв-ся,т.к. обрыв цепи происходит при столковении актив.частиц в объёме реакцион.смеси на пылинках(или др. массив.частицах).При дав-ях,равных Р₂, смесь взрыв-ся,т.к. число разветвлений цепей выше числа их обрывов на третьих частицах.3-ий предел взрыв-ти происходит при Р₃(повышение дав-я смеси) и обусловлен тепловой природой процессов,особ-но легко он проходит для экзотермич.р-ций.При сжатии смесей происходит их сильный разогрев,к-рый приводит к их взрыву.Тепловому взрыву способ-ют каталит.действи стенок сосуда,на к-рых при адсорбции могут создаваться актив.частицы.Особ-ть ц.р.- наличие периода индукции в превращении исх.смеси в-в.За время периода идукции в смеси накаплив-ся а.ч.,к-рые приводят к постепенному развитию ц.р. с послед. взрывом. . P₁,P₂,Р-предел.дав-я взрыва и общ.внеш.дав.Т₀-постоянная.При Р< P₁ и P> P₂ T₀<0→затух-щий пр-с,при P₁<Р< P₂ T₀>0→пр-с протекает с самоускорением.Т-хар-ет вр,в теч к-рого конц-я промеж. продуктов увел-ся в е раз. Вр,в теч. к-рого скорость пр-ся переходит от незначительной неизмер.вел. к оч.большой измер.величине.

56.Основные признаки катализа. Катализ – явление изменения скорости реакции в присутствии веществ – катализаторов, которые вступают в промежуточное взаимодействие с реагирующими веществами, но в процессе реакции не расходуются и в состав конечных продуктов не входят. К. участвует в образовании активированного комплекса. К. не может вызвать изменение энергии Гиббса, следовательно, не может вызвать протекание реакции. В состоянии равновесия К. в равной степени ускоряет прямую и обратную реакции.Специфичность катализа заключается в том, что реакции данного типа ускоряются К. лишь определенного химического состава. Так, кислотно-основные реакции ускоряются кислотами или основаниями, а ОВР – переходными металлами или их соединениями (особенно высоким каталитическим действием обладают элементы 8 группы). Специфичность обусловлена характером связей (ковалентная, донорно-акцепторная, водородная), которые возникают между катализатором и реагентом.

57.Свойства катализатора.(К)К-в-во,к-рое,участвуя в элементар. стадиях хим.пр-са(х.р),изменяют скор-ть х.р.,и после завершения р-ции сами остаются хим-ки неизмен-ми.Физич. и текстурное состояние К может меняться.К,взаим-я с молекулами реагентов,обмен-ся с ними энергией и электронами.К могут снижать Е_а и создавать благоприят. для взаим-я ориентацию мол-л.Элементар.акт может проходить т-ко м\у активир.м-ми.Роль К при возбуждении м-л реагентов сводится к изменению их орбитальной симметрии.К явл-ся в-во,если:1)в-во должно влиять на изменение скор-ти х.р. при небольших его сод-ях в реакцион.смеси.Если в-во проявл-ет каталит.св-ва,то оно циклически участвует в элементар.стадиях превращ-я мол-л реагентов.2)скор-ть х.р. меняется в завис-ти от конц К в реакцион.см. К участвует в образ-нии нестойких промежуточных соед-ний с м-ми реагентов. Ниж. предел каталитич. действия в-в зависит от природы и строения м-л реагир. в-в и К. Если К участвует в катализе с обр-ем промеж.комплекса(КС),то при равновес. сод-нии КС в смеси,скор. х.р. будет прямо пропорц-на конц.К.Если К участвует во взаим-вии с предварит-но возбужд. м-ми,то скор. х.р. может выражаться нулевым,дроб,положит,отриц порядком по конц К в завис-ти от его кол-ва в реакц.см. При нулевом порядке для конц. К происходит “выпадение” его из реакц.см. (скрытый катализ 1 рода).Если “выпадает” конц. одного из реагента и К,то возникает скрыт.катализ 2 рода.При отриц порядке по конц К скор-ть х.р. убывает и происходит самоотравление К или ингибирование К–ром нек-рых реагентов.3)К,не смещая положения хим.равновесия в реакц.см.,способ-ет сокращению времени его достижения.Он одновременно влияет на скор-ть прям. и обрат. р-ций.К участвует т-ко в возбужд. м-л реаг. полем своих актив.центров и способ-ет снижению стерич.препятствий взим-вию возбуж.м-л.4)Подверг-ся воздействию ядов и ингибиторов.Яды по дейсвию подразделяют: избирательные (выключ-ся отдел.ф-ции К);обратимые (происходит при умеренном связывании м-л яда актив.центрами);необратим(при прочном связывании);накапливающ-ся(при медлен накоплении яда на пов-ти К в ходе р-ции).Для описания закономер-тей отрав-я энергетич.однород. пов-тей тв.К: ,А,А₀-актив-ть отрав-го и исход.К;α-эмпирич.коэф-т;Г-кол-во яда.Для неоднород.пов-тей: ; g-число м-л яда;z₀-обл-ть миграции м-л яда на пов-ти К;β=g_эф/g-вер-ть отравления актив.центра;g_эф-число м-л яда,отрав-щих актив.ц.Отравляющее действие завис. от тем-ры,дав-я,природы и сп-ба приготовления К.Выше 973К отрав-е не происходит,т.к. яды разлаг-ся,а К полностью теряют актив-ть из-за структур. изменений.5)Селективность- св-во К. ускорять р-цию лишь по одному из возможных путей.Селек-ть зависит от условий проведения и степени завершенности р-ции. ;x_i-выход i-го цел.продукта,х-общ.превращ-е сырья. Чем выше селек-ть,тем меньше затрачивается энергии.6)Промотирование и модифицирование К. В-ва,к-рые сами явл-ся каталитически актив.,но при добав-нии к-рых к К повыш-ся его актив-ть,наз. промоторами.Если при изменении добавок в-в в К актив-ть его вначале растёт,достигает макимума, а затем сниж-ся,то такие в-ва наз.модификаторами. ;w₀-скор х.р. без добав.;∆w₀-прибав к скор за счёт добав,R-критерий модиф-я.R>w₀-модиф.К, R<w₀-отрав-е.Промоторы могут изменять струк-ру К,состояние каталит.центров, способствовать появл-ю модиф-ции с повыш.каталит. актив-тью.При повыш тем-рах или невыс.конц в кач-ве промотора примен-ют яды.7)К не участвует в общ стехиомет-рии р-ции.

58.Общий и специфич. кислотно-основ.катализ.К кисл.-основ. кат-зу отн-ся пр-сы изомеризации,гидратации и дегидратации,гидолиза,этерификации и др. При бимол-ной гетерогенной катал-кой р-ции 1 из частиц явл-ся акцептором (электрофил), другая – донором (нуклеофил) пары электронов. Чем более ярко выражены св-ва электрофильности и нуклеофильности, тем выше скорость р-ции.В завис-ти от природы частиц, выступающих в качестве К., реакции кислотно-основного типа делятся на: 1. специфический кислотный катализ, включает реакции, катализируемые только ионами водорода (гидроксония). 2. специфический основный катализ, включает реакции, катализируемые ионами гидроксила. 3. общий кислотно-основной катализ, включает реакции, катализируемые любыми кислотами и основаниями Бренстеда. 4. электрофильно-нуклеофильный катализ, включает реакции, катализируемые акцепторами или донорами электронных пар.В общ случае скор. х.р.,проводимой в р-ре (вод. или невод) может повыш-ся под воздействием Н⁺,ОН^-,Ме⁺,А^-.МА(соль),к-ты,основания.Урав-е кинетики для р-ции представ-ся: .Первый член отражает некатал-кое превращ-е в-ва.Для выявл-я влияния кажд.компонента на скор х.р. проводят раздельно в кисл.ср.,в р-ре соли и в р-ре основ.Для каждого компоненте состав-ют соответ. ур-е р-ции: ; ; . Если кат.р-ции проводятся в р-рах с неидеальными св-вами,то вместо конц примен-ся актив-ти,причём скор. х.р. в завис-ти от ионной силы р-ра будет изменяться по слож.з-ну.Каталит.актив-ть слаб.к-ты может повыш-ся солями этой к-ты.Такой эффект наз-ся вторичным солевым эф-том.Нейтральные соли могут изменять каталит.действие к-ты за счёт изменения ион.силы р-ра и степени сольватации м-л и ионов в р-ре.Под воздействием м-л нейтр.соли скор.х.р. может увел-ся,умен-ся или остав-ся неизмен.При р-ции гидролиза нейтр.соли не влияют на скор.х.р.: lgk_э=lgk₀.Для р-ции лигандного обмена скор.х.р. повыш-ся lgk_э=lgk₀+4√j.Для р-ции окис-я брома скор.умен-ся lgk_э=lgk₀-√j,где k_э,k₀-константы скор в присут-вии соли и в её отсут-вии.k₀=к₁К_с-произвед-етистин.константы скор. И конст. Ав-сия;j-ион.сила р-ра.Изменение скор.х.р. в р-ре под действием к-ты и нейтр.соли за счёт изменения ион.силы р-ра наз-ют первич.солевым эф-том(прибавление нейтр.соли,не имеющей общего иона с катал-щей р-цию к-той).

59.Катализ КС переходных металлов и ферментатив.катализ.В кач-ве К примен-ся КС катионов переход.Ме(Vlll гр. Fe,Co,Ni,Ru,Pd и др).Сущ-ть каталит.действия заключ-ся в том,что ионы Ме с d-электрон. конфигурацией d⁶-d¹⁰ могут взаим-ть с др.м-ми,выступая,как акцепторы и доноры электронов.Ионы перех.Ме могут взаим-ть с несколькими лигандами.Число лигандов завис.от строения лиганда и электрон.конфигурации иона Ме.В р-ции А₁+А₂→А₃+А₄,катал-емой комплексными К,м-лы реагентов выступают как лиганды по отнош. к иону Ме. Хим.взаим-вие м\у м-ми А₁ и А₂,координир-ми около центр.иона Ме ,облегчается благодаря поляризации м-л,понижению энергии отдельных связей и повыш.вер-ти оптимального расположения реагир.м-л.Центр.ион Ме явл-ся мостиком,облегчающим электрон. переходы м\у реагир. м-ми.Катал.актив-ть иона Ме зависит от энергии связи иона с участниками р-ции.Если эн.св. М-L велика или мала,то ион Ме прояв-ет слаб.каталит.актив-ть.В 1-ом случ. м-лы так прочно соед-ся с ионом Ме,что блокируют его и выводят из р-ции.При низ.энергии связи реагир.м-лы не смогут вытеснить из КС др. присут-щие в р-ре лиганды,при к-ром энергетич.возмущение м-л,вошедших в состав КС,недостаточно.Являясь донорами или акцепторами элек-нов,одни лиганды могут сущ-но влиять на распред-е электрон.плотности в др.реагир.м-лах,вошедших вместе с ними в состав КС,и изменять эн-ю отдел.связей.Эти св-ва лигандов и ионов Ме дают возможность регулир-я каталит.актив-ти ионов введением в коорд.сферу лигандов определ-го строения.Лиганды,повыш-щие катал.акт-ть иона Ме в дан.р-ции,наз. активаторами,пониж-щие-ингибиторами.Координационно-насыщенные КС не явл-ся актив.К.Ферменты-белки,вход.в состав клеток и тканей,кат-щие х.р.,протек-щие в орг-ме.Они отлич-ся высок. каталит.актив-тью,специфич-тью,избират-тью.Ф.к.-явление более сложное и высокоорганиз-ное,чем обыч катализ.Высок. организ-ть пр-сов ф.к. опред-ся особ-тью хим.взаим-вия в орг-ме,вызываемой сочетанием актив.центра ферм-та и субстрата.В актив.катал.центр входят группы,к-рые могут ориентир-ть м-лы субстрата в опред-ном положении по отнош. к актив.ц. Актив.ц. ф-та имеют строго опред-ную струк-ру.Они сод-т актив.гр.-доноры или акцепторы электронов.Многие в-ва оказ-ют на ф-ты активир. и ингибир. действие(ионы тяж.Ме отравляют почти все ф-ты).Каталит.актив-ть ф-тов проходит ч\з максимум при измен. рН.В сильнокисл. и сильнощел.средах ф-ты теряют катал.актив. вследствие денатурации белка.В обл.0-40ºС скор.р-ций,кат-мых ф-тами,при повыш-нии тем-ры возрастает в соот-вии с ур.Аррениуса.При тем-рах 60-70ºС белки денатурируются и полностью теряют катал.актив-ть.

60Кинетика гомогенных катал. р-ций Гомогенными назыв. такие реакции, при котор. все реагир. в-ва и kat наход-ся в одной и той же фазе, например, в газовой или в р-ре; при этом атомы, молекулы или ионы реагирующих в-в взаимод-вуют по всему занятому объему. В этих пр-сах роль kat формально сводится к снижению Еа и, сл-но, к ускорению р-ции. Кроме того, участие kat в пр-се приводит к усложнению кинетического закона протекания р-ции. Рассмотрим для примера бимолекулярную р-цию, идущую в присут-вии kat.

A+B+K↔^R1_R2 ABK*. Скорость пр-са в целом опред-ся скоростью распада активного комплекса в направлении образования продуктов р-ции и регенерации kat:ABK*→^R3 K+Продукты

Кон-ция активного ком-са:[ABK*]= (R1[A][B][K])/(R2+R1[A][B]

Скорость пр-са в целом:-d[A]/dt=R3*[ABK*]=(R3R1[A][B])/ /(R2+R1[A][B])*[K]

Если равновесие м/у исх. в-вами и активным комплек-сом сдвинуто в сорону активного ком-са, т.е. R1>>R2, то и R1[A][B]>>R2

-d[A]/dt=R3*[K] Если – в сторону исходных в-в, то R2>>R1[A][B] и тогда

-dA]/dt=(R3R1)/R2*[A][B][K] во всех случаях скорость пр-са пропорциональна кон-ции kat.

61.З-ны Фика и роль диффузии в гетерог.катал.р-циях.Гетероген.пр-с можно разделить на 5 стадий:1)транспорт реагир.в-в к пов-ти К(диф-зия);2)адс-ция реагир.в-в на пов-ти К;3)р-ция на пов-ти К;4)десорбция продуктов р-ции с освобождением пов-ти К;5)транспорт продуктов р-ции в объёме(диф-зия).В завис-ти от условий провед-я пр-са и его особ-тей наиб.медленной стадией может быть любая из 5.Для гетероген.пр-сов особую важность приобретает перемещение в-ва из внутрен.объёма ж-ти или газа к тв.пов-ти,т.к. гетероген. хим. р-ция может протекать в том случае, если происходит непрерывная молекулярная или конвективная диффузия реагирующих в-в к поверх-ти, на кот. идет данная р-ция, и непрерывная диф-зия продуктов р-ции.Диф-ный пр-с имеет чисто физич.природу и его можно описать с пом. з-нов Фика:dn/dt=-D*S*(dc/dl) (1); dn/dt=-D*S*(d²c/dl²) (2),n-кол-во в-ва,проход-го ч\з площадку размером S за вр t;D-коэф-т мол-ной диф-зии,м²*с^-1.1-ый з.Фика опр-ет,что скор. диф. пр-са в неподвижной среде в изотермич.условиях ч\з слой толщиной δ прямо пропорц-на градиенту конц-ции в-ва.Отриц.знак в (1) показ-ет убыль конц-ции;коэф-т D при малых конц-ях не завис. от конц.в-ва С. 2-ой з.Фика опр-ет скор.накопления в-ва в дан. системе за опред-ное вр.Коэф-т диф-зии опр-ся как отнош. квадрата средней длины пробега м-л ко вр.диф-зии и он обратно пропорционален давлению: D=l²_сред/2t.Градиент конц. в-в в потоке можно представить в форме конечной разности: -dn/dl=(c_s-c_x)/l (3).Подставим (3) в (1): dn/dt=D*S*((c_s-c_x)/l); c_s,c_x- конц в-ва в объёме и у пов-ти К,моль\м³.Скорость диф-зии возрастает с повыш.тем-ры по з-ну,аналог.ур.Аррениуса: D=ke^-E/RT.Но величина Е во много раз меньше Е_а большин-ва х.р.→с повыш тем-ры скор.диф-зии будет расти значит-но медленнее,чем скорость х.р.

62.Области протекания гетероген.катал.р-ций. Гетерогенная хим. р-ция может протекать в том случае, если происходит непрерывная молекулярная или конвективная диффузия реагирующих в-в к поверх-ти, на кот. идет данная р-ция, и непрерывная обратная диф-зия продуктов р-ции.Скор. пр-са будет опр-ся скор. лимит-щей стадии.Если скор. хим. р-ции > скор. диф-зии, то скорость пр-сса в целом будет опред-ся скор-тью диф-зии. В этом случае пр-с лежит в диф-оной области и кинетика р-ции подчиняется урав-ям, к-рые рассматр-ют пр-сы диф-зии.Пр-с при этом чаще всего опис-ся ур-ем 1-го порядка,т.к. скор.диф-зии прямо пропорц-на конц. Если скор. х. р. < скор. диф-зии, то скорость р-ции опр-ся скоростью хим. р-ции. Тогда пр-с лежит в кинетической области и описывается урав-нием кинетики той р-ции, к-рая проходит на повер-ти К. Если скорось диф. и скорость хим. р-ции, рассмотренные независимо друг от друга, соизмеримы, то имеется переходная область.Она хар-ся тем,что конц. реагир.в-в в центре зерна меньше,чем на наруж пов-ти зёрен К.В перех.обл. порядок и Е_а измен-ся от измен. тем-ры,к-рое происходит от тем-ры, опр-мой кинетич.обл.,до тем-ры,хар-ной для диф.обл.Большое влияние на хар-р протекания гетер.х.р. оказ-ют давления реагир.в-в,скор. потоков,пористость К и тем-ра.При изменении тем-ры на 10ºС скор. диф-зии измен-ся ≈в 1,2 раза, а скор.х.р.- в 3-4раза→при понижении тем-ры скор.х.р. убывает быстрее,чем скор. диф-зии,и при низких тем-рах пр-с чаще протекает в кинетич.обл.Если не все участки пов-ти, на к-рой протекает р-я в равной степени доступны для реагир.м-л,то часто оказ-ся,что на части пов-ти р-я протекает в кинетич.обл,а на остальной-в диф-ной.При проведении р-ции на неравнодоступ.пов-ти возмож.4 обл.1)Внеш.диф.обл. (Скор.диф. м-л к внеш. пов-ти К-лимит.ст).Внешдиф.обл. проявл-ся,когда пр-с проводится при повыш. тем-рах,при наличии у пов-ти К плёнки,затруд-щей подход м-л реаг-тов к актив.ц. К,при проведении пр-са в присут-вии высокоактив.К. В случ. внеш.диф. конц-ии регаир.в-в на пов-ти пористого тела и внутри пор гораздо меньше,чем в объёме.2)Внутр.диф.При таком режиме конц. реагир. в-в у внеш.пов-ти пористого К близки к конц. их в объёме;конц в порах уменьш-ся от наруж. пов-ти зёрен пористого К к их центру,а конц. прод.р-ции соот-но возрастает.Кин-ка пр-са завис. от соотнош. внеш и внутр пов-ти;если они соизмеримы,то кин-ка соот-ет промеж.обл.Внутридиф.пр-сы опис-ся ур-ем массопереноса: w_м.п.=β∙S(c^п-с^об),β=D/l-коэф-т массопер-са; c^п-конц в-ва у пов-ти,на входе в пору,с^об-конц в-ва в объёме пор.3)Внеш.кинетич.обл.(Скор. х.р. м\у адсорбир.в-ми на внеш. пов-ти К гораздо меньше скор. пр-сов на др. стадиях). Конц. реагир. в-в на пов-ти К и в объёме равны,но р-я протекает т-ко на внеш пов-ти К.Кин-ка пр-са опр-ся кин-кой х.р.Состав-ся ур-я завис-ти скор.х.р. от тем-ры, конц К и др.параметров.4)Внутр.кинетич.обл.(наиб медл.стадия-ст. хим. превращ-я м-л реагентов,адсорбир-ных на актив.ц. внутри пор К).При таком режиме конц в-в в объёме,на пов-ти К и внутри пор одинаковы.Кин-ка опр-ся к-кой пр-са.Скор.пр-са зависит от всей пов-ти К(внутр. и внеш).А во внешнекин.обл. т-ко от внеш.

63.Кин-ка гетероген.кат.р-ций,к-рые не тормозятся продуктами р-ции.Будем рассмат-ть р-ции на тв.К,в к-рых реагир.в-ва и продукты р-ции газообраз.В типич.гетероген.пр-се регир-ют т-ко те в-ва,к-рые адсорбир-ны на пов-ти.Скор.гет.х.р. опр-ся как кол-во в-ва,реагир в ед. вр. на ед. площади пов-ти К:υ=dx/Sdt,x-кол-во в-ва,прореагир. к моменту вр t,моль;S-общ.площадь пов-ти К,на к-рой идёт х.р.Скор. гет.х.р. прямо пропорц-на пов-ной конц в-в,к-рая прямо пропорц-на степени заполнения пов-ти θ→ dx/Sdt=θ.Т.к. пов-ть дан.К постоянна, то величину общ.пов-ти К можно ввести в константу скор.k’, т.е. k’S=k → dx/dt=kθ(1).Величину пов-ти,занятую реагир.в-вом на 1 см² пов-ти К,можно найти,исходя из ур-я:θ=Kp/(1+Kp)(2),p-дав-е газа,К-константа рав-сия адсорб-ции(адсорб.коэф-т).Из(2) след.,что если адс-ция мала,то θ<<1,и К<<1,поэтому Кр в знаменателе пренебрегаем.Тогда из (2): θ=Кр(3),т.е. при малых дав-ях пов-ть,занятая адсорбир. в-вом,прямо пропорц-на дав-ю.Эта обл. наз-ся обл-тью линейной адс-ции.Если адс-ция велика,то Кр>>1,и в знаменателе (2) пренеб-ем 1→θ=1(4)-ур-е асимптоты кривой,опис-мой ур-ем (2).Если реаг-ет одно в-во и его адс-ция мала,то,подставив в (1) знач-е θ из(2):dx/dt=kKp(5).Пусть kK=k*→выр-е (5) примет вид:dx/dt=k*p(6). p=n_i/V *RT=(n₀-x)/V *RT(7),n_i= n₀-x-число грамм-мол-л исх.в-ва в момент вр. t,n₀-в начальн.момент,V-общ объём системы.Подставим (6) в (5) и получим ур-е,удобное для интегрирования(k*-кажущаяся константа скор.пр-са).Подставим (2) в (1): dx/dt=k*∙(p/1+Kp).Это выр-ние соответ-ет случаям,когда реагир.в-во адсорб-ся умеренно:dx/dt=k*p^1/n.Такой дробный порядок явл-ся кажущимся.Он получ-ся,т.к. в кин-кое ур-е вводим величины,хар-щие изменение конц.в-ва не непосред-но на пов-ти,а в объёме.В наше выр-е входит не пов-ная конц,хар-мая велич.θ,а величина,хар-щая сод-е реагир.в-ва в объёме-его парциальное дав-е р.Если реагир. в-во сильно адс-ся,то θ=1,тогда подставив (4) в (1):dx/dt=k(кажущ-ся порядок равен 0,р⁰=1).

64.Связь м\у истинной и кажущ-ся энериями активации.Если построить на основании экспер-ных данных график завис-ти кажущ-ся константы скорости k* от 1/T,то получ-ся прямая,опис-мая ур-ем:lnk*=-E*/RT+lnc или dlnk*/dt=E*/RT²(1),где E*-кажущ-ся Е_а.Найдём завис-ть м\у Е_а и E*. k*=kK.Адсорбцион.коэф-т(константа рав-сия) К равен отнош. констант скоростей пр-сов адс-ции и десорб-ции:К=k₁/k₂, k*=k∙ k₁/k₂(2).Каждая из констант,входящих в (2),явл-ся функцией тем-ры.Т.к. k₁=C’/√T(C’-величина постоянная), k₂=C”e^-λ/RT(3)(C”-велич.постоян.,λ-т-та адсорбции),k=Ce^-E/RT(4).Константа скорости пр-са адс-ции k₁ с тем-рой измен-ся очень мало по срав-ю с k и k₂.Завис-тью k₁ от тем-ры можно пренебречь и считать,что эта величина постоянная.Подставив (3) и (4) в (2):k*=Ce^-E/RT∙k₁/(C’e^-λ/RT)→lnk*=-E/RT+λ/RT+lnconst (const=Ck₁/C’). Дифференц-ем по Т:dlnk*/dT=(E-λ)/RT²(5)/Сравнивая (5) и (1),видим: Е*=Е-λ(6).Это выр-е хар-ет завис-ть кажущ-ся Е_а от истин. Е* меньше Е_а на величину т-ты адс-ции реагир.в-ва.Для простешей р-ции А→В на пов-ти тв.К можно выделить с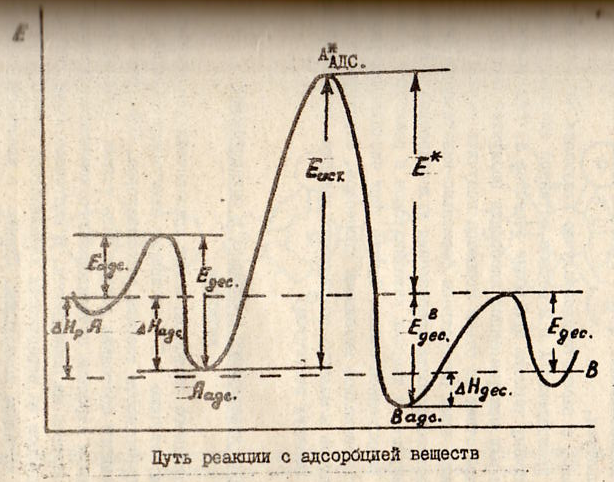 тадии:А→А_адс→А*_адс →В_адс→В. Вначале м-лы в-ва А адс-ся на пов-ти тв.К,преодолевая энерг.барьер Е_адс.Выделяя избыток энергии в форме т-ты адс-ции,м-ла может перейти в более уст-вое адсор-ное сост.А_адс.На новом кат-ком центре или под воздействием актив.центра К м-ла А может перейти в электронно-возбуждённое сост с переходом на энергетический барьер высотою Е_ист.(А*_адс).Возбуждённые м-лы А,скатываясь в ложбину продукта р-ции,превращ-сяв прод.р-ции.При этом м-ла В переходит в адсорбир.сост.Для десорбции м-лы В с актив.ц. ей необх-мо преодолеть энергию Е^В_адс.После чего м-ла В может уйти с каталит.центра в объём реакцион.смеси.

65.(1)Основные теории катализа: мультиплетная, ансамблей, электронная, радикальная.

1.Мультиплетная. Основные положения этой теории:

1.Активный центр кат-ра представляет собой совокупность определенного числа адсорбционных центров, расположенных на поверхности в геометрическом соответствии со строением мол-лы, претерпевающей превращение(принцип геометрического или структурного соответствия).

2.При адсорбции реагирующих мол-л на активном центре образуется мультиплетный комплекс, в рез-те чего происходит перераспределение связей, приводящее к образованию продуктов реакции.

Для различных реакций число адсорб.центров в активном центре принимается равным 2,3,4,6.подобные акт.центры были названы дублетами,триплетами,квадруплетами,секстетами, а в общем мультиплетами.

Второе исх.положение явл. принцип энергетического соответсвия (Баландин),согласно к-ому энергия активации гетерог.р-ции явл.сложной вел-ной,в первом приближении состоящей из 2х слагаемых,одно из к-ых зависит только от энергии связи между составными частями реагир.в-в,а другое-от энергии вз-ия между катализатором и составными частями мультиплетного комплекса.Гетерог.р-ция представлена след.образом:

Исх.в-ва+кат-тор→мультипл.комплекс→кат-тор+продукты р-ции

Для I стадии необходима энергия разрыва связей,при этом выделяется энергии образования мультипл.комплекса.Е=разность этих энергий.

Для II стадии необх.энергия для разрыва связей в мультипл.комплексе. выделяется энергия обр-ния конечных продуктов.Разность этих энергий определяет скорость II стадии.

2.Ансамблей

Основное исх.положение – носителем каталит.активности явл. находящаяся на пов-ти атомная(докристаллич) фаза кат-ра,относительно к-ой пов-ть носителяч(или кристалл.фаза самого кат-ра) выполняет функцию инертной подкладки. Для каждого данного процесса акт.центром явл. ансамбль из определенного числа n атомов кат-ра.

Теория акт.ансамблей дает возможность,исходя из опытной зав-ти активности от концентрации кат-ра на пов-ти носителя,определить число n атомов в акт.центре,число Z_n, областей миграции и абсолют.производительность r_n акт.центра для данного процесса.

Зав-ть активности от концентрации

3.Электронная

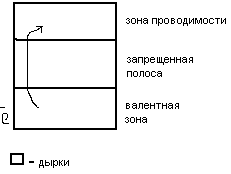Для полупров-ков.Эл-ны-носит.эл-ва, при перемещ.в тв.теле остав.дырки(вакан.орбит.) Ток возможен если недостат.эл-ов в связях или в реш.есть изб.эл-нов. При электрич-ве эл-ны и дырки движ.в разл.направл. Они вызыв.превращ.акцепт.и дон.

65(2)

мол-л реагента. Пр-с кат-за превращения включ.стадию хемосорбции на пов-ти тв.кат.,мол-ла реаг.в-ва- акцептор (дырка). Эл-ны или дырки уч.в созд.нов.мол-лы с пов-тью тв. тела. Акцепт.связь- образ.эл-ном пов-ти и акцепт.мол-лой (Сеα). Дон.связь- образ.своб. дыркой реш.тв.тела и донор.ат. Если ат.сорбир.без уч.эл-на или дырки-слабая связь. Зонная теор.строения тв.тел: при объедин.орбит.соседних ат.мет. возник.2 осн.зоны. Заполн.эн.ур-ни – валентная зона(система дырочн.ур-ней), вакант.эн.ур-ни- зона провод-сти(система эл.уровней. Эти зоны отделены запрещ. зоной. На пов-ти п/п может адс.акцепт.мол-ла, кот.притяг.эл-н из решетки,вал.зоны или на нее выпад.эл-н из зоны пров-сти.(Следовательно,происходит адсорбция на донорной или акцепторной связи е и дырки перемещ.поэтому слабые связи переходят в прочные и наоборот. Недостатки:хорошо для полупроводников,но не всегда применимо к др.в-вам.)

4.Радикальная

На пов-ти мет.и п/п сод.радикалоподобные состояния ат.и мол. (нескомпенсир.вал-сти) Радикал(вал-сть) явл-ся нициат. цепи(обозн.V) Реакция .вида: A₂+B₂= 2AB

Стадия а: A₂+V  AV + A (инициир.цепи)

Стадия б: A + V  (A) связыв.атома вак.вал-стью

Стадия в: (A) + AV  A₂ + V регенерация радикала

Стадия г: B₂+ V  BV + (B)

Стадия д: (B) + BV  B₂+ V

Стадия е: (B) + V₂ B +V ((В) может также реаг.на акт.ц. А):

Стадия ж: (A) + BV  AB+V

Стадия з: (B) +AV  AB +V; c А и В реаг.физич.адсорб.А₂иВ₂:

Стадия и: (A) + (B₂) AB + (B)

Стадия к: (B) +(A₂)  AB + (A)

Обрыв цепи-путем рекомб.своб.вал-стей:

(A)+(A) = A₂

(B)+(B) = B₂

₍(A)+(B) = AB

V + V = V₂ ск-сть отдельн.стадий р-ции завис.от велич.эн-гии связи A-V, B-V и теплот р-ций на стадиях а и г (Qav, Qbv). Теплоты вз-ия центров с мол-ми А₂ и В₂ опр-ся по разности между энергиями связей Qav и Qaa и Qbb

q1=Qav-Qaa

q`2=Qbv-Qbb

Для кажд.пары эн-гии св. Qaa и Qbb пов-сть тв.кат.должна облад.меньшими велич. Е св. атомов с кат.ц. Qav и Qbv.

66.Что называется носителем, промотором, активным центром?

Промотор - вещ-во к-ое само по себе каталитич. недеятельное, но вызывает повышение эфф-ти пр-са(повышение активности кат-ра). Эф-сть зав.от его кол-ва: наблюд.максимумы акт-ти при опред.составе смеш.кат-ра. Явл.промотир.на практ.повыш.акт-сть, срок действ.и избират. кат-ра. Метал.кат-р работает своей пов-стью (малая доля всей массы кат-ра). Поэтому примен.адсорбц.кат-ры (наносят тонкий слой акт.в-ва на недеят.носитель. Различают стуктурообразующие (стабилизируют активную фазу кат-ра по отношению к нагренванию или др.воздействиям.) и модифицирующие промоторы (изменяют строение и хим.состав активной фазы).

Носитель- в-ва с высокоразв.пов-стью (уголь,силикагель,пемза,стекло) Он может в небол.пределах.изм.акт-ть кат-ра,проявляя опред.промотир.эф-кт. Устойч.адс.кат.к темп.и отравл.ядами повышается чем у мет.кат. Чтобы актив.кат-р его прогревают,но это мож.привести к спеканию. Носитель препятсв.спеканию,благодаря этому можно повыш.темп-ру проведения пр-са. Актив.компл.на кат.адсорбируются, но активна не вся пов-сть а только отд.участки-активн.центры. Число акт.ц. влияет на ск-сть пр-са.

Носитель для каталитически активных фаз выполняют роль матрицы,на к-ой формируется активная фаза.они могут участвовать в создании новых фаз,регулировать строение,состав полиэдров и число окисления катиона в составе полиэдра.

Актив.центры-атомы,спосбн.образовыватьпромежут.соед. (активир.комплексы)

Активный центр - особая часть молекулы фермента, определяющая её специфичность и каталитическую активность.

Активный центр непосредственно осуществляет взаимодействие с молекулой субстрата или с теми её частями, которые непосредственно участвуют в реакции.

67.Уравнение динамики нестационарных процессов.

Уравн.динамики-2 переменных-время и координата. Рассмотрим поток хим.реаг.в-в, проход.через сеч.L₁ и L₂, наход.на расст.ΔL. В потоке хим. р-ция: Темп.в реак-ре постоянна. Площадь сечения потока ρ. Лин.ск-сть потока в люб.сеч. u, а конц.в-ва Ai в люб.сеч.C(Ai). Эти величины переменные. Y(Ai) –кол-во в-ва Ai, реаг.к моменту времени t в любом задан.объеме V/ Тогда общ.уравнение димнамики проц.в потоке в режиме ид.выт.:

Пользуясь векторн.обознач.запишем:

68.Уравнение кинетики односторонней р-ции, проводимой в реакторе идеального вытеснения.

Ид.вытес.в потоке - когда фронт газ. смеси в трубке имеет плоский профиль и отсутств. продольн.и попереч. перемеш. смеси диффузией. В реакц.трубку сечением ρ(s1) (1см²) поступает поток в-в с конц.в-ва Ai- c(Ai) и проходит с лин.ск-тью V(м/с). За время dτ через сеч.ρ(s1) (1см²) пройдет в-во А в кол-ве с(Ai)V dτ. Т.к. нестац.усл(кол-во в-ва на входе в р-р меняется во врем.), кол-во в-ва Ai,проход.через сеч.l на расст. l+dl запишем так: где 2ой член-накопл.в-ва в заданном объеме. Определим это накопление:

Qнакопл.=Qрасход (расписать). Получаем: . При пост.ск-ти подачи сырья (стац.усл) прав.часть=0. . V=V(a)/ρ(s), c(Ai)=n(Ai)/V(a). V(a)-об.ск-сть перемещ.реакц.смеси,м³/с. n(Ai)-кол-во исх. Ai, кот.проходит ч/з сеч.р-ра на расст.l от начала реакц.зоны, моль/с. Подставив, получим:

. Если n(A)=n(A0)(1-x), где n(A0)-мольн.ск-сть подачи в-ва Ai в р-р, моль/с:

69.Кинетика гомогенных реакций, проводимых в условиях идеального перемешивания.

Если в реактор, объем (V) кот. может изменяться, вводят смесь реаг.в-в с объемн. скоростью V₁ и отбирают с объемн.скор. V₂, то кол-во молей любого в-ва в реак-ре будет изм-ся во времени. Конц.в-ва A_i на входе = Coa_i. При ид.перемеш. конц.в-ва на выходе из реакт. такая же как и в любой точке внутри него (Сa_i). w-истин.ск-сть хим.р-ции по в-ву A_i. Ур-ние мат.баланса:

Реактор пост.объема, жидк.в-ва. Имели объем V₀ вначале,затем будет расти до объема реакт. . Подставляя получим

- ск-сть хим.р-ции при увелич. объема реаг.смеси. w=k*f*(C_A1…C_Ak),эксперим.рассчит.конст. ск-стей хим.р-ций.

Если в РИП р-ция в газ.фазе:

Откуда - ск-сть р-ции при изм.давл. в реак-ре (давл.газов растет и раст.число молей A_i).Для ид.газов:

p-общ.давл.в р-ре в данный момент врем. ∑n-общ.число молей в р-ре в данный момент времени.

Стацион.сост.в р-ре в жид.фазе при пренебреж.изм.плотности в-в V₁=V₂=V => dV/dt=0. => V=const. V₀=V_p=> число молей в р-ре не зависит от времени => dC_Ai/dt=0.

Для газ.фазы причем V₂ не произвольна, иначе давл.в р-ре будет имз.со врем.и пр-с не будет стацион.

На выходе: на входе:

Для жид.фазы(V₁=V₂):

Для обратим.р-ций:

Для необр.

Система послед.соед.РИП-выходы прод-тов приближ.к выходам прод-тов пр-са в 1-ом РИВ.

70. Кинетика реакций, проводимых в растворе.

При рассмотрении процессов в растворах необходимо учитывать структуру и природу растворителя и растворенного вещества, структуру, химический состав раствора и условия протекания реакции.

Растворители бывают полярные или неполярные Растворы: ионные и молекулярные, концентрированные и разбавленные, идеальные и неидеальные. Структура чистых жидкостей – пространственные группы молекул (тетраэдр, тригональная бипирамидальная, октаэдр и др). Из сочетания 2-х, 3-х и более полиэдров создается ансамбль полиэдров. Число молекул растворителя, окружают такую же молекулу или ион – координационное число. При растворении в растворителе жидкости, газа или тв. вещества происходит их диспергирование до молекул или ионного состояния. Молекулы или ионы растворенного вещества занимают пустоты в полиэдрах или разрушая их, создают новые.

Реагирующее вещество вступает не в форме индивидуальных молекул, а в форме сольватов. Молекула движется в «клетке» из молекул растворителя, движение колебательное и, следовательно, число столкновений больше, чем в газе, т. к. молекулы плотно упакованы в жидкости. W= kc_iⁿⁱ, k зависит от природы растворителя. Мономолекулярные реакции в жидкостях и в газовой фазе происходят с одинаковыми скоростями.

Пусть в растворе протекает реакция: A+B A..B C , раствор неидеальный.

По ЗДМ или ,где a и y – активности и коэффициенты активности

Концентрация переходного состояния: . По теории переходного состояния , h-постоянная Планка При получим Скорость химической реакции зависит от природы растворителя. Так при y=10 скорость реакции в растворе в 10 раз выше чем в газовой фазе.При y=1 скорость реакции в растворе = скорости в газовой фазе.

Для мономолек.р-ции A  A* -> продукты и при получим:

, т.е. скорость реакции не зависит от природы растворителя.

71.

Влияние ионной силы на скорость реакции, проводимой в растворе.

Во всех уравнениях химической кинетики фигурируют кон­центрации реагирующих веществ. В термодинамике же константа равновесия неидеальной системы выражается через активности. Это обстоятельство необходимо учитывать, если в кинетическое уравнение входит константа равновесия. Правда, при реакциях в газовой фазе и между нейтральными молекулами в растворе в этом нет практической необходимости, но при рассмотрении ре­акций между заряженными частицами подобное пренебрежение может явиться источником существенных ошибок.

Для константы скорости бимолекулярной реакции A+ В → AВ* → продукты

протекающей в растворе, теория активного комплекса, _;дает

κ=χ

Термодинамическая константа равновесия между исхешшми ве­ществами и активным комплексом κ^*= =

Комбинируя уравнения, получим уравнение Бренстеда — Бьеррума: κ=χ =К₀ для константы скорости реакции, протекающей в любой неидеальной среде. Величина К₀ имеет смысл константы скорости при бес­конечном разведении, т. е. при γ= 1.

Если в качестве стандартного со­стояния выбрать бесконечное разведение, теория электролитов дает следующее приближенное соотношение для коэффициента активности: γ= ,где А — постоянная≈ 0,51; z —заряд иона; I— ионная сила раствора; β — некоторая постоянная, примерно обратно пропорциональная радиусу иона.

Если z_A и z_B — соответствующие заряды реагирующих частиц, то реакция может быть записана в виде A^Za+B^zb→AB*(^Za+Zb) → продукты

а подстановка соответствующих значений коэффициентов, актив­ности в уравнение Бренстеда — Бьеррума дает

Рассмотрим два случая.

1. Взаимодействие между заряженными части­цами.

Сумма мала, и для случая взаимодействия между двумя ионами ими можно пренебречь, т. е.

Следовательно, логарифм константы скорости, согласно теории должен быть линейной функцией корня квадратного из ионной силы, а тангенс угла наклона прямой определяется соотношением зарядов реагирующих частиц.

2. Взаимодействие между ионом и нейтральной молекулой

Согласно уравнению γ= , коэффициент активности для нейтральной молекулы γ= и для реакции A+B^zb→AB*(^Zb) → продукты

получаем

Следовательно, константа скорости дол­жна быть прямо пропорциональна ионной силе. Зависимость константы скорости реакции от ионной силы называют первичным солевым эффектом. Вторичный солевой эффект (в случае слабых электролитов) – скорость реакции изменяется вследствие изменения одного из реагирующих присутствующих посторонних электронов, изменяющих ионную силу раствора и соответственно степень диссоциации реагирующего электролита.

72. Влияние природы растворителя и давления на скорость химической реакции, проводимой в растворе.

При рассмотрении процессов в растворах необходимо учитывать структуру и природу растворителя и растворенного вещества, структуру, химический состав раствора и условия протекания реакции.

Растворители бывают полярные или неполярные Растворы: ионные и молекулярные, концентрированные и разбавленные, идеальные и неидеальные. Структура чистых жидкостей – пространственные группы молекул (тетраэдр, тригональная бипирамидальная, октаэдр и др). Из сочетания 2-х, 3-х и более полиэдров создается ансамбль полиэдров. Число молекул растворителя, окружают такую же молекулу или ион – координационное число. При растворении в растворителе жидкости, газа или тв. вещества происходит их диспергирование до молекул или ионного состояния. Молекулы или ионы растворенного вещества занимают пустоты в полиэдрах или разрушая их, создают новые.

Реагирующее вещество вступает не в форме индивидуальных молекул, а в форме сольватов. Молекула движется в «клетке» из молекул растворителя, движение колебательное и, следовательно, число столкновений больше, чем в газе, т. к. молекулы плотно упакованы в жидкости. W= kc_iⁿⁱ, k зависит от природы растворителя. Мономолекулярные реакции в жидкостях и в газовой фазе происходят с одинаковыми скоростями.

Пусть в растворе протекает реакция: A+B A..B C , раствор неидеальный.

По ЗДМ или ,где a и y – активности и коэффициенты активности

Концентрация переходного состояния: . По теории переходного состояния , h-постоянная Планка При получим Скорость химической реакции зависит от природы растворителя. Так при y=10 скорость реакции в растворе в 10 раз выше чем в газовой фазе.При y=1 скорость реакции в растворе = скорости в газовой фазе.

Для мономолек.р-ции A  A* -> продукты и при получим:

, т.е. скорость реакции не зависит от природы растворителя.

Конст. равновесия (V-изменяется обратно в результате реакции)

тогда

По теории АК: , логарифм. и дифф. по реакции:

или (Vизменяется обратно активности)

(если ΔV<0- константа скорости увеличивается с ростом давления)

Если график зависимости lnk от давления прямая,то δv не зависит от давления.

Получим: k(0)- константа скорости при нулевом давлении.

73.Кинетика гетерогенных каталитических реакций, которые тормозятся продуктами реакции.

Продукты могут адсорбироваться на поверхности; катализатора и тем самым уменьшать поверхность, занятую реагирующим веще­ством. Это будет приводить к торможению процесса. Поэтому при расчете поверхности, занятой реагирующим веществом, следует учитывать адсорбцию продуктов распада.

Если адсорбируются два вещества А и В, то можно написать θ=Кр

,где К_А и К_в; р_а и р_В — адсорбционные коэффициенты и парциальные давления веществ Аи В. *

Если реагирует только одно вещество и реакция на поверхности следует уравнению первого порядка (истинный порядок), то уравнение кинетики хими­ческого процесса запишется следующим образом:

Рассмотрим несколько примеров расчёта,, основанного на использовании уравнения.

I. Реагирующий газ адсорбируется слабо, продукт реакции — умеренно. Из этих исходных условий вытекает, что К_А р_А ‹‹1, этой величиной можно пренебречь, т. е. →

где k* = кК_А— кажущаяся константа скорости реакции.

Примером реакции, кинетика которой подчиняется этому уравнению яв­ляется реакция распада закиси азота N₂O на платине. Процесс распада тормозится кислородом.

2. Реагирующее вещество адсорбируется слабо, продукт реакции — сильно. В этом случае, согласно сказанному выше, К_А р_А ‹‹1 , а К_ВР_В ›› 1→ и, следовательно, ,где k* = k(k_A/k_B).

Примером такого процесса может служить разложение аммиака на пла­тине. 3. Реагирующее вещество и продукт реакции адсорбируется сильно. Тогда К_А р_А ››1 , а К_ВР_В ›› 1 и, следовательно: → , где k* = kК_A

Примером такой реакции является реакция дегидратаций этилового спирта на окиси алюминия.

Если два реагирующих вещества адсор­бируются па одинаковых адсорбционных центрах и истинный порядок реакции — второй, то общее уравнение кинетики можно записать следующим образом:

74.Кинетика гетерогенных каталитических реакций, проводимых в реакторе идеального вытеснения.

Реакторы проточного типа могут применяться двух типов: пустотелые или имеющие распределительные решетки. Процессы в таких реакторах проходят в потоке, в реакторе идеального вытеснения реакционной смеси с неподвижным слоем катализатора или в потоке. В этом случае через слой неподвижного шарикового или движущегося с малой скоростью катализатора сырье проходит в поршневом режима, то есть, когда предыдущий слой сырья вытесняет передний его фронт.

Скорость гетерогенной каталитической для режима идеального вытеснения

Гидродинамический РИВ реакционной смеси может соблюдаться для реактора, в котором отношение длины его к диаметру больше пятидесяти (l / d > 50). Уравнения скорости реакций, протекающей в потоке, можно получит на основе анализа уравнения потока массы веществ.

Гомогенный поток массы веществ в нестационарных условиях, находящийся под воздействием конвективной силы к в котором проходит химическая реакция:

(1),где - объемно-молекулярная концентрация, N_A, V_A-мольная и объемная скорости подача веществ,V - линейная скорость перемещения потока веществ,

w - скорость химической реакции в гомогенной сис­теме, τ-время.

Для перехода к уравнению потока массы веществ через слой зернистого катализатора необходимо учитывать тот факт, что вещество перемещается только между зернами катализатора.

Вводим коэффициент , определяющий долю площади реактора, свободной от катализатора.

S_0V-площадь единицы объема катализатора. Умножим уравнение (1) на /S_0V

Введем обозначение

Запашем концентрацию и лилейную скорость через соотношения: ; V=Va/Ps*χ. Ps-площадь раствора в сечении Получим:

Для стащюиарных условий (для равномерной подачи сырья в реактор) концентрация вещества А не меняется со временем по длине реактора И тогда первая производная по времени будет равна нулю

Уравнение потока массы веществ для стационарных условий:

Уравнение скорости химической реакции, протекающей в потоке, в гетерогенной, системе, для РИВ. Если количество непрореагировавшего вещества А обозначить как , тогда n⁰_а –мольн.скорость подачи А.

х-превращение, моль/моль. Это ураанв&ао скорости было выведено впервые АД,Баландиным и повторено с теоретическим выводом Г.М.Дакчевкоаым,

Скорость гетерогенной каталитической реакции зависит от количества сорбированного катализатором вещества, от давления, темперы, природы катализатора, наличия в реакционной смеси астехиометрических компонентов и других факторов. Скорость гетерогенной каталитической реакции будет прямо пропорциональна поверхностной концентрации реагирующих веществ, возведенных в степень соответствующих порядку реакции. Для Уравнение кинетики.:

П-знак произведения., θ-относительные поверхностные концентрации веществ.

2