Цепи синусоидального тока

1. Нарисовать временную диаграмму sin-тока,дать определение амплитуды,периода,частоты,круговой частоты,нач.фазы.Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 2.1).i(t) = I_m sin(ωt - ψ_i). I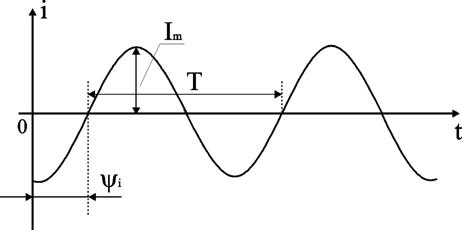 _m– максимальное значение синусоидальной функции (амплитуда);

T – расстояние между 2-мя точками, фазы колебания которых отличаются на величины 2π (период колебаний); f=1/T – величина, обратная периоду (частота); F=50Гц, Т=0,02с W=2 πf – угловая (круговая) частота Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения.Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на  рад., то угловая частота есть , где f– частота.   - начальная фаза - значение фазы в начальный момент времени (t=0);

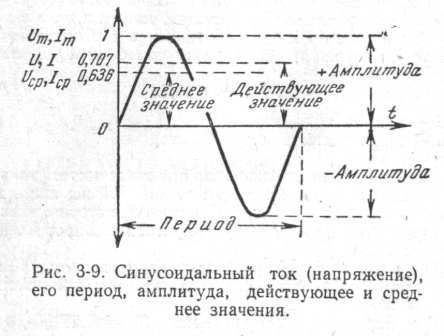
2.Дать определение интегральных величин:среднего,среденевыпрямленного,действующего значения переменных токов.Средним значением синусоидального тока (напряжения) называется среднее арифметическое всех его значений за полупериод. Оно равно 0.636 амплитудного значения или 0.9 действующего значения, т.е. Iср = 0,636 Im = 0,9 I  Uср = 0,636 Um = 0,9 U 

Среднее значение синусоидального тока (напряжения) за период равно нулю, так как на протяжении пер­вого полупериода ток имеет одно направление, а на про­тяжении второго полупериода - обратное. Однако в случае двухполупериодного выпрямления переменного тока в постоянный ток имеет одинаковое направление, и вели­чина выпрямленного тока определяется именно средне­арифметическим всех мгновенных значений.

Действующие значения тока и напряжения соот­ветствуют величине постоянного тока, выделяющего в одном и том же активном сопротивлении такое же коли­чество тепла. Действующие значения I и U синусоидаль­ного тока и напряжения равны соответственно:I = 0,707 Im; U = 0,707 Um 

3.Пояснить физ.смысл действующих значений переменного тока и напряжения.Действующее значение переменного тока численно равно такому постоянному току, при котором за время, равное одному периоду в проводнике с сопротивлением R выделяется такое же количество тепловой энергии, как и при переменном токе.

Действующее или эффективное значение переменного тока рав­но силе такого постоянного тока, который, протекая по дан­ному проводнику, выделяет в нем ежесекундно то же количе­ство энергии в виде тепла, что и переменный ток.

Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых до­стигает переменный ток, но и от формы тока.

Для гармонических колебаний тока Для любой из синусоидальных величин получаем Условились, что все измерительные приборы показывают действующие значения. Например, 220 В – действующее значение, тогда  .

4 .Изобразить векторную диаграмму тока. Как она связана с временной?Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

5.Дать определение:мгновенная мощность,активная мощность.Построить графики.Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи. P(t)=U(t)*I(t)Мощность переменного тока.В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол   (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность. Единица измерения — ватт (W, Вт).Среднее за период   значение мгновенной мощности называется активной мощностью:  . В цепях однофазного синусоидального тока  , где   и   — среднеквадратичные значения напряжения и тока,   — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи   или её проводимость   по формуле  . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепейэлектрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью   активная связана соотношением  .Мощность в цепи синусоидального тока. Активная мощность. При изменении тока и напряжения в течение периода мощность p = ui, потребляемая двухполюсником при токеi = I_m sin (t + _i) и напряжении на зажимах u = U_m sin (t + _u) также будет переменной в течение периода.Мгновенная мощность

имеет постоянную составляющую — среднюю за период активную мощность   и переменную синусоидальную составляющую .Активная мощность, потребляемая двухполюсником при синусоидальном токе, зависит не только от напряжения и тока, но и от угла фазового сдвига  между ними. Для индуктивного и емкостного элементов при  = ±  /2 активная мощность равна нулю, так как эти элементы в течение отдельных частей периода лишь накапливают энергию и затем отдают ее другим элементам.Изменение мгновенной мощности p(t), потребляемой произвольным двухполюсником, иллюстрируется графиком (сплошная красная линия на рис. 7.7).

И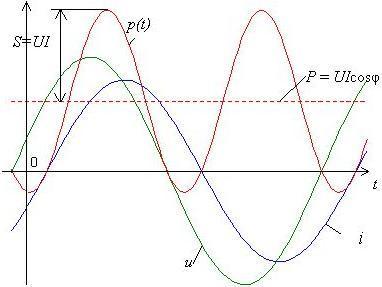 з него следует, что мгновенная мощность изменяется по синусоидальному закону с частотой, равной удвоенной частоте тока и напряжения.