Построение конечных полей с помощью неприводимых многочленов

{(3) – слайд 67}

• Выбираем простое p и фиксируем поле

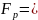
• Образуем кольцо 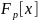многочленов над ним.

• Выбираем натуральное n и неприводимый многочлен

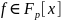• Идеал порождает фактормножество , элементы которого суть совокупность остатков от деления многочленов на 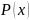: 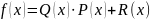. Множество является полем Галуа – расширение n-ой степени поля 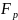(обозначается ).

Пример: построение поля (слайд 71).

Полиномиальное и степенное представление элементов поля.

Любой элемент циклической группы можно представить как степень примитивного элемента. Пример: слайды 265 и далее.

Алгоритм нахождения всех корней многочлена f(x) над полем 𝔽𝑝.

Минимальные многочлены для элементов конечного поля. Алгоритм нахождения минимального многочлена.

Определение минимального многочлена.

{(3) – слайд 129} Рассмотрим поле , а в нем — какой-нибудь элемент β и будем интересоваться многочленами, для которых этот элемент является корнем. Многочлен m(x) называется минимальной функцией (или минимальным многочленом, м.м.) для β, если m(x) —нормированный многочлен минимальной степени, для которого β является корнем.

Алгоритм нахождения минимального многочлена.

Теорема Хэмминга. Пример построения кода Хэмминга.

Теорема Хэмминга.

{(1) – стр. 172} При 2r < n максимальное число t кодовых слов находится в пределах 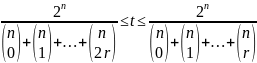r – максимально допустимое число ошибок. n – длина кода.

Пример построения кода Хэмминга.

{(1) – стр. 173} n = 2^q – 1, r = 1. Для q = 3 построим код Хэмминга (длины 7). Построим таблицу: слева – диагональная матрица размерности 2^q – (q+1), справа все бинарные наборы длины q, содержащие не менее 2-х единиц. Складывая по mod 2 произвольные совокупности строк, получаем 16 различных бинарных наборов, которыми можно закодировать 16 сообщений.

1	0	0	0	1	1	0
0	1	0	0	1	0	1
0	0	1	0	0	1	1
0	0	0	1	1	1	1

Коды бчх: определение, примеры кодов с исправлением одной, двух и трех ошибок. Определение кода бчх.

{(3) – слайд 402 и далее} Циклический код, исправляющий кратные (2 и более) ошибки. {(5) – стр. 5} Пусть 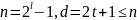. Тогда кодом БЧХ называется (n, k, d)-линейный циклический код, в котором порождающий многочлен g(x) определяется как минимальный многочлен для элементов из поля 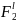, где 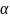– произвольный примитивный элемент поля . Схема построения:

• Строим поле 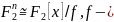неприводимый многочлен степени n = 2^m – 1.

• Выберем в циклической группе 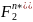примитивный элемент и рассмотрим его степени 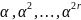, где r – количество ошибок, которые надо исправить.

• В разложении многочлена 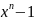выберем такие неприводимые многочлены, чтобы каждая из указанных степеней была корнем одного из них (не всегда возможно). Тогда

1. есть результат перемножения этих многочленов;

2. коды — коэффициенты многочленов из идеала – исправляют r ошибок.