Прикладная алгебра. Суровый теормин.

Оглавление

Понятие группы, подгруппы, факторгруппы, индекса группы по подгруппе. Примеры. Теорема Лагранжа. 3

Группа. 3

Подгруппа. 4

Факторгруппа. 4

Индекс группы по подгруппе. 4

Примеры 4

Теорема Лагранжа. 4

Понятие циклической группы. Структура подгрупп циклической группы. Количество порождающих элементов. 4

Циклическая группа. 4

Структура подгрупп циклической группы. 4

Количество порождающих элементов. 4

Понятие кольца, подкольца, факторкольца, евклидова кольца, идеала в кольце. Примеры. 5

Кольцо. 5

Подкольцо. 5

Факторкольцо. 5

Евклидово кольцо. 5

Идеал в кольце. 5

Примеры 6

Расширенный алгоритм Евклида и его применение. 6

Понятие поля. Построение конечных полей с помощью неприводимых многочленов (привести пример). Полиномиальное и степенное представление элементов поля. 6

Поле. 6

Построение конечных полей с помощью неприводимых многочленов 6

Полиномиальное и степенное представление элементов поля. 7

Алгоритм нахождения всех корней многочлена f(x) над полем 𝔽𝑝. 7

Минимальные многочлены для элементов конечного поля. Алгоритм нахождения минимального многочлена. 7

Определение минимального многочлена. 7

Алгоритм нахождения минимального многочлена. 7

Теорема Хэмминга. Пример построения кода Хэмминга. 7

Теорема Хэмминга. 7

Пример построения кода Хэмминга. 7

Коды БЧХ: определение, примеры кодов с исправлением одной, двух и трех ошибок. 8

Определение кода БЧХ. 8

Код с исправлением одной ошибки. 8

Код с исправлением двух ошибок. 8

Код с исправлением трех ошибок 8

Коды БЧХ: общая схема декодирования. 8

Понятие действия группы на множестве, фиксатор и стабилизатор. Примеры. 9

Действие группы на множестве. 9

Фиксатор. 9

Стабилизатор. 9

Примеры 9

Лемма Бернсайда и её применение. 9

Лемма Бернсайда. 9

Применение. 9

Цикловой индекс действия группы. 9

Группы симметрий правильных многоугольников (диэдральные группы) и группы вращений правильных многогранников. Примеры. Их цикловые индексы. 10

Теорема Редфилда-Пойа и её применение. 10

Идеалы и фильтры частично упорядоченного множества. Конусы. Точные грани. 10

Частично упорядоченное множество. 10

Порядковый идеал. 10

Порядковый фильтр. 10

Верхние и нижние конусы и грани. 10

Главные идеалы и фильтры. 10

Точные грани. 11

Теорема Шпильрайна. Линейное продолжение частично упорядоченного множества. 11

Теорема Шпильрайна. 11

Линейное продолжение частично упорядоченного множества. 11

Спектр и размерность частично упорядоченного множества. 11

Спектр частично упорядоченного множества. 11

Размерность частично упорядоченного множества. 11

Фундаментальная теорема о конечных дистрибутивных решётках. 11

Соответствия Галуа. 11

Источники 11

Понятие группы, подгруппы, факторгруппы, индекса группы по подгруппе. Примеры. Теорема Лагранжа. Группа.

{(1) – стр. 12} Группа G = <M, ∗> — это такая пара из множества M и бинарной операции ∗ на этом множестве, что выполняются следующие свойства (аксиомы группы):

• G1: (x ∗ y) ∗ z = x ∗ (y ∗ z ) (ассоциативность);

• G2: (аксиома единицы) существует единственный единичный элемент e такой, что для любого x выполняется e ∗ x = x ∗ e = x;

• G3: для любого элемента x существует ровно один обратный элемент, т. е. такой элемент y, для которого y ∗ x = x ∗ y = e (обратный элемент обозначается x⁻¹).

Подгруппа.

{(1) – стр. 24} Пусть G – группа, и для какого-то множества выполнены свойства:

• 

• Если , то

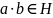
• Если 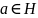, то

H называется подгруппой G.

Факторгруппа.

{(1) – стр. 52} Группа смежных классов группы G по нормальному делителю H.

Индекс группы по подгруппе.

{(1) – стр. 28} Количество смежных классов группы G по подгруппе H называется индексом подгруппы и обозначается через (G : H).

Примеры

Теорема Лагранжа.

{(1) – стр. 29} Пусть H — подгруппа группы G. Тогда порядок H является делителем порядка G: |G| = (G : H) · |H|.

Понятие циклической группы. Структура подгрупп циклической группы. Количество порождающих элементов.

Циклическая группа.

{(1) – стр. 22} В циклической группе есть такой элемент (он называется порождающим элементом группы), что каждый элемент группы может быть получен (многократным) применением групповой операции к порождающему.

Структура подгрупп циклической группы.

{(1) – стр. 30} Всякая подгруппа циклической группы — циклическая.

Количество порождающих элементов.

{(2)} У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция Эйлера.

Понятие кольца, подкольца, факторкольца, евклидова кольца, идеала в кольце. Примеры.

Кольцо.

{(1) – стр. 85} Кольцо — это множество R с двумя бинарными операциями сложения + и умножения · такими, что

• R1: относительно сложения R — коммутативная группа (которая называется аддитивной группой кольца);

• R2: умножение ассоциативно; (в других источниках может не быть аксиомой – могут выделяться отдельно ассоциативные кольца)

• R3: a · (b + c) = a · b + a · c; (b + c) · a = b · a + c · a (дистрибутивность умножения относительно сложения слева и справа).

Если в кольце имеется единичный элемент для умножения, то кольцо называется кольцом с единицей. Если умножение коммутативно, то такое кольцо называется коммутативным кольцом.

Подкольцо.

Такое подмножество кольца, которое является подгруппой по сложению и замкнуто относительно операции умножения.

Факторкольцо.

{(2)} Пусть I – идеал кольца R. Определим на R отношение эквивалентности: 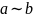тогда и только тогда, когда 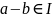. Класс эквивалентности элемента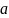 обозначается как 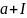. Факторкольцо R|I – множество классов смежности элементов кольца R по модулю его идеала I, на котором определены операции сложения и умножения:

• (a + I) + (b + I) = (a + b) + I

• (a + I) · (b + I) = ab + I