Политропный процесс
Все рассмотренные выше термодинамические процессы являются частными случаями обобщенного политропного процесса.
Уравнение политропного процесса
где n – постоянное число для рассматриваемого процесса и называется показателем политропы.
Количество политропных процессов бесконечно велико, и каждому процессу соответствует свое значение показателя политропы. В общем случае он может принимать значение в интервале – ∞ < n < + ∞.
При n →±∞ уравнение политропы будет выражать изохорный процесс. Для доказательства этого представим уравнение политропного процесса в виде
(1.88б)
извлечем корень n-й степени из обеих частей уравнения (1.88б) и получим
(1.88в)
При n →±∞, p→1, следовательно v1 = v2, то есть v = const
Если
показателю n придать значение равное
нулю (n = 0), то 
и уравнение политропы превращается в уравнение изобарного процесса р = const.
При n = 1 уравнение политропы (1.88а) принимает вид уравнения изотермы рv = const, а если n = k, то уравнение
Уравнение политропного процесса выводится на основе уравнений первого закона термодинамики dq = du + pdv и
dq = di – vdp, внутренней энергии u = cvT и энтальпии i = cpT
dq = cdT = cvdT + pdv = cpdT – vdp. (1.89)
Отсюда следует
(с – сv)dT = рdv и (с – ср)dT = – vdр.
Обозначим
Тогда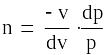 
Или
После интегрирования уравнения (1.90) при n = const получим
то есть уравнение политропного процесса будет иметь вид
Изменение внутренней энергии в любом процессе идеального газа определяется уравнением u2 – u1 = cv(T2 – T1).
Изменение энтальпии можно найти из уравнений
i = u + (p v) и i = cpT
i2 – i1 = (u2 – u1) + [(p2v2) – (p1v1)] = cp(T2 – T1). (1.93)
Теплоемкость политропного процесса вычисляется из уравнения
Тогда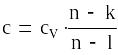 
Где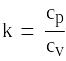 
-показатель адиабаты
Количество теплоты, подведенной (отведенной) в политропном процессе
dq = cdT, значит q = c(T2 – T1). (1.95)
Работу в процессе можно получить из определения работы
и уравнения политропного процесса
Получим
Бесконечное множество политропных процессов можно разделить на три группы (I, II, III) (рисунок 1.16).
Для первой группы (I) (при – ∞ < n < +1) характерно то, что в процессах расширения теплота расходуется на изменение внутренней энергии и на совершение работы против внешних сил. В процессах сжатия, наоборот, теплота выделяется во внешнюю среду за счет уменьшения внутренней энергии и совершения работы сжатия внешними силами.
Процессы второй группы (II) (при + 1 < n < + k) отличаются тем, что работа расширения в них производится за счет внешней теплоты и за счет изменения внутренней энергии. В процессах сжатия затраченная работа частично переходит в эквивалентное количество теплоты, отводимой во внешнюю среду и на увеличение внутренней энергии.
В процессе третьей группы (III) (при κ < n < + ∞) при расширении внутренняя энергия расходуется на выполнение работы и теплоту, отводимую в окружающую среду, при сжатии – наоборот.
Для нахождения изменения энтропии в политропном процессе воспользуемся первым (dq = du + pdv) и вторым (ds = dq/T) законами термодинамики
(1.97)
Интегрируя уравнение (1.97), получим
