10. Элементы специальной теории относительности. Постулаты Эйнштейна. Преобразования Лорнеца. Изменения размеров тел, собственного времени и массы в релятивистских случаях. Связь массы и энергии.

Специальная теория относительности — теория, описывающая движение, законымеханики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, —релятивистскими скоростями.

Основные понятия

Система отсчёта представляет собой некоторое материальное тело, выбираемое в качестве начала этой системы, способ определения положения объектов относительно начала системы отсчёта и способ измерения времени. Обычно различают системы отсчёта и системы координат. Добавление процедуры измерения времени к системе координат «превращает» её в систему отсчёта.

Инерциальная система отсчёта (ИСО) — это такая система, относительно которой объект, не подверженный внешним воздействиям, движется равномерно и прямолинейно. Постулируется, что любая система отсчёта, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, также является ИСО.

Событием называется любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x, y, z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т.п.

Обычно рассматриваются две инерциальные системы S и S'. Время и координаты некоторого события, измеренные относительно системы S, обозначаются как (t, x, y, z), а координаты и время этого же события, измеренные относительно системы S', как (t', x', y', z'). Удобно считать, что координатные оси систем параллельны друг другу, и система S' движется вдоль оси x системы S со скоростью v. Одной из задач СТО является поиск соотношений, связывающих (t', x', y', z') и (t, x, y, z), которые называются преобразованиями Лоренца.

Постулаты Эйнштейна

В основу специальной теории относительности Эйнштейна легли два постулата, т.е. утверждения, которые принимаются за истинные в рамках данной научной теории без доказательств (в математике такие утверждения называются аксиомами).

1   постулат Эйнштейна или принцип относительности: все законы природы инвариантны по отношению ко всем инерциальным системам отсчета. Все физические, химические, биологические явления протекают во всех инерциальных системах отсчета одинаково.

2  постулат или принцип постоянства скорости света: скорость света в вакууме постоянна и одинакова по отношении» к любым инерциальным системам отсчета. Она не зависит ни от скорости источника света, ни от скорости его приемника. Ни один материальный объект не может двигаться со скоростью, превышающей скорость света в вакууме. Более того, пи одна частица вещества, т.е. частица с массой покоя, отличной от нуля, не может достичь скорости света в вакууме, с такой скоростью могут двигаться лишь полевые частицы, т.е. частицы с массой покоя, равной нулю.

Преобразования Лоренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов.

Преобразования Лоренца псевдоевклидова пространства сигнатуры   находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского).

Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты   каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.

Если ИСО   движется относительно ИСО   с постоянной скоростью   вдоль оси  , а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:

где   — скорость света, величины со штрихами измерены в системе  , без штрихов — в  .

Относительность одновременности

Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта  , то они будут неодновременны относительно «неподвижной» системы  . При   из преобразований Лоренца следует

Если  , то и  . Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого  . Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве.

Пусть в двух системах отсчёта вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов (на рисунке ниже) они показывают одинаковое время.

Левый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (правый рисунок).

Сокращение линейных размеров

Если длину (форму) движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются:

,где   — длина вдоль направления движения относительно неподвижной системы отсчёта, а   — длина в движущейся системе отсчёта, связанной с телом (т.н. собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.

Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения.

Масса и энергия покоя связаны уравнением:

E = mc² из которого вытекает, что всякое изменение массы  Δm  сопровождается изменением энергии покоя  ΔE₀  ΔE₀ = Δm c²

^{Это утверждение носит название закона взаимосвязи массы и энергии покоя, оно стало символом современной физики}

11. Колебательное движение. Гармонические колебания и принципы их сложения. Понятие о теореме Фурье. Упругие колебания. Дифференциальное уравнение свободных гармонических колебаний. Характеристики собственных колебаний. Вынужденные колебания. Резонанс.

Колебательное движение это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени.

^.Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или ,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд   — полная фаза колебаний,   — начальная фаза колебаний.Обобщенное гармоническое колебание в дифференциальном виде

 Сложение гармонических колебаний

        Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.

Метод векторных диаграмм

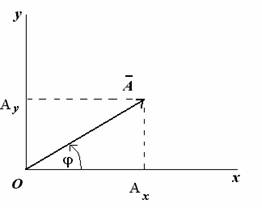         Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = wt + j₀ где j₀ - начальный угол.

Проекции вектора А на оси координат запишутся:

        Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу.

        Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

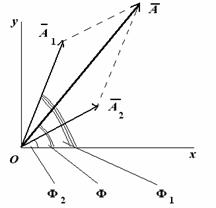         Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

        Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f(фаза результирующего колебания).

        Из очевидных геометрических соображений находим:

        Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности  . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

         Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

    Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот   - частотой биений (циклической).

        При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x). например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

     В общем случае это - уравнение эллипса. При A₁=A₂ - окружность, при   (m - целое) - отрезок прямой.

        Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Понятие о теореме Фурье?????? Что? Такого нет в учебнике… и в инете все стремно Т__ Т только ряды Фурье из матана Т__Т

Упругие колебания

У маятника возвращающая сила обязана своим возникновением силе тяжести. Но для колебаний существенно только само наличие возвращающей силы, т. е. такой силы, которая всегда направлена к положению равновесия и, вообще говоря, увеличивается с удалением от этого положения. Такого рода силы возникают также при деформации твердых тел и представляют собой упругие силы. Следовательно, эти упругие силы тоже могут вызывать колебания. По происхождению возвращающей силы такие колебания называются упругими. Колебания тела, подвешенного на пружине, вагона на рессорах, пластинки, зажатой в тиски, колебания камертона, натянутой струны— все это упругие колебания. В соответствии с иным происхождением возвращающей силы потенциальная энергия упругих колебаний естьэнергия деформации упругого тела, а не потенциальная энергия силы тяжести, как у маятника. В остальном динамика упругих колебаний та же, что и у маятника. И здесь мы имеем дважды за период переход кинетической энергии в потенциальную (энергию деформации) и обратно. При не слишком больших амплитудах эти колебания являются гармоническими, причем период их выражается формулой, аналогичной формуле математического маятника: Здесь m — масса колеблющегося груза, k — жесткость пружины, т. е. сила, необходимая для растяжения пружины на единицу длины.

Дифференциальное уравнение гармонических свободных колебаний имеет вид   .Для интегрирования этого линейного однородного дифференциального уравнения с постоянными коэффициентами составим характеристическое уравнение   ,  его корни  .

Так как корни мнимые, общее решение дифференциального уравнения имеет вид:

.

Дифференцируя полученное решение по времени, получим второе уравнение для определения постоянных интегрирования   .С учетом начальных условий:  ,      имеем   ,    .Рассмотрим другой вид записи общего решения, для чего введем следующую подстановку:

,   , тогда получим    .

Свободные прямолинейные колебания материальной точки происходят по гармоническому закону («по закону синуса»). При этом:  − амплитуда колебаний,  − начальная фаза колебаний,     циклическая или круговая частота свободных колебаний,  - период свободных колебаний,  − частота колебаний (количество колебаний за одну секунду).

Частота и период свободных колебаний не зависят от начальных условий движения.

Рассмотрим движение точки в среде с сопротивлением, пропорциональным скорости,  под действием линейной восстанавливающей силы ( ). 

В этом случае       −     дифференциальное уравнение  затухающих колебаний.

Характеристическое уравнение, соответствующее данному дифференциальному уравнению, имеет вид:    , его корни  .

Если    (случай малого сопротивления), то корни комплексные и общее решение дифференциального уравнения имеет вид:   ,

 или в амплитудной форме:     .Множитель   указывает на то, что амплитуда колебаний с течением времени уменьшается. Такие колебания называютсязатухающими. Период затухающих колебаний    ,

где   − период свободных колебаний без сопротивления.Если  , то сопротивление практически не влияет на период колебаний  .

Рассмотрим влияние сопротивления на изменение амплитуды колебаний. Определяя максимальное отклонение точки от положения равновесия для двух моментов времени, отличающиеся на период  , находим   ;     или       

Характеристики собственных колебаний

Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Характеристики

Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы,   (м) Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание),   (с) Частота — число колебаний в единицу времени,   (Гц, с⁻¹).

Период колебаний   и частота   — обратные величины; и 

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота   (рад/с, Гц, с⁻¹), показывающая число колебаний за   единиц времени:

Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения — метр. Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:  .

Гармони́ческийосцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука): , где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде:  . Если ввести обозначения:   и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже полученоздесь и оно имеет вид: ,где   — произвольные постоянные, которые определяются из начальных условий.Найдём частное решение. Для этого подставим в уравнение решение вида:   и получим значение для константы:

Тогда окончательное решение запишется в виде:

Резонанс

Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде:  . Подставим этот анзац в дифференциальное уравнение и получим, что : Таким образом, колебания в резонансе будут описываться следующим соотношением:

12. Упругие волны. Монохроматическая волна, ее формула и характеристики. Суперпозиция бегущих волн. Стоячие волны. Эффект Доплера. Звуковые волны. Инфра- и ультразвуки, их применение. Сейсмические волны и их детектирование.

Упругие волны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.

В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.

В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.

В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.

Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.

Наиболее распространёнными типами упругих волн в твёрдых телах являются:

продольные волны — волны с колебанием частиц вдоль направления распространения волны;

поперечные волны — волны с колебанием частиц перпендикулярно направлению распространения волны;

поверхностные волны (например волны Рэлея — волны с колебанием частиц по эллипсам вдоль поверхности тела;

волны Лэмба — волны в тонких пластинах;

изгибные волны — распространение колебаний деформации изгиба в стержнях или пластинах, длина волны которых много больше толщины стержня или пластины.

Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте.

Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Бегущая монохроматическая волна

Вектор Умова-Пойнтинга S= [ExH] — вектор, направление которого совпадает с направлением распространения энергии в электромагнитной волне, а модуль |S| равен потоку энергии.

Стоячая монохроматическая волна

Стоячая монохроматическая волна — волна, формирующаяся при распространении двух плоских монохроматических электромагнитных волн одинаковой поляризации навстречу друг другу.

В общем случае уравнение монохроматической волны имеет вид

.

Где а – амплитуда, - начальная фаза, - круговая частота.

Помимо характеристик, общих с гармоническим колебанием: амплитуды, круговой частоты, частоты и периода Т, у монохроматической волны есть еще две характеристики – длина волны и волновое число.

Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой .

Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной, групповая скорость которой отлична от нуля, связан перенос энергии, импульса или других характеристик процесса.

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе.

Бегущая волна — волновое возмущение, изменяющееся во времени и пространстве согласно выражению где — амплитудная огибающая волны, — волновое число и — фаза колебаний. Фазовая скорость этой волны даётся выражением где — это длина волны.

Стоячая волна является частным случаем бегущей волны с .

То есть, две одинаковые периодические бегущие волны (в рамках справедливости принципа суперпозиции), распространяющиеся в противоположных направлениях, образуют стоячую волну.

Стоячая волна — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

, где u — возмущения в точке х в момент времени t, — амплитуда стоячей волны, — частота , k — волновой вектор, — фаза.

Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.

При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.

Эффект Доплера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.

Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.

Для волн (например, звука), распространяющихся в какой-либо среде, нужно принимать во внимание движение как источника, так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, в вакууме имеет значение только относительное движение источника и приёмника.

Математическое описание

Е сли источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается:

где — частота, с которой источник испускает волны, — скорость распространения волн всреде, — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником

А налогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника

где — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

П одставив вместо в формуле (2) значение частоты из формулы (1), получим формулу для общего случая:

Звук — физическое явление, представляющее собой распространение в виде упругих волнмеханических колебаний в твёрдой, жидкой или газообразной среде. В узком смысле звуком называют субъективное восприятие этих колебаний специальными органами чувств животных или человека.

Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16—20 Гц до 15—20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, от 1 ГГц — гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).

Различают продольные и поперечные звуковые волны в зависимости от соотношения направления распространения волны и направления механических колебаний частиц среды распространения.

Коэффициент затухания отражает быстроту убывания амплитуды с течением времени. Если обозначить время, в течение которого амплитуда уменьшается в е = 2,718 раза, через , то:

Уменьшение амплитуды за один цикл характеризуется логарифмическим декрементом. Логарифмический декремент равен отношению периода колебаний ко времени затухания :

С корость звука в любой среде вычисляется по формуле:

г де — адиабатическая сжимаемость среды; — плотность.

Ультразвук — упругие колебания с частотой за пределом слышимости для человека. Обычно ультразвуковым диапазоном считают частоты выше 18 000 герц.

Хотя о существовании ультразвука известно давно, его практическое использование достаточно молодо. В наше время ультразвук широко применяется в различных физических и технологических методах. Так, по скорости распространения звука в среде судят о её физических характеристиках. Измерения скорости на ультразвуковых частотах позволяет с весьма малыми погрешностями определять, например, адиабатические характеристики быстропротекающих процессов, значения удельной теплоемкости газов, упругие постоянные твердых тел.

Диагностическое применение ультразвука в медицине (УЗИ)

Благодаря хорошему распространению ультразвука в мягких тканях человека, его относительной безвредности по сравнению с рентгеновскими лучами и простотой использования в сравнении с магнитно-резонансной томографией ультразвук широко применяется для визуализации состояния внутренних органов человека, особенно в брюшной полости и полости таза.

Помимо широкого использования в диагностических целях, ультразвук применяется в медицине как лечебное средство.

Ультразвук обладает действием:

-противовоспалительным, рассасывающим

-аналгезирующим, спазмолитическим

-кавитационным усилением проницаемости кожи

Резка металла с помощью ультразвука

На обычных металлорежущих станках нельзя просверлить в металлической детали узкое отверстие сложной формы, например в виде пятиконечной звезды. С помощью ультразвука это возможно, магнитострикционный вибратор может просверлить отверстие любой формы. Обычно резьба сначала делается в мягком металле, а потом уже деталь подвергают закалке. На ультразвуковом станке резьбу можно делать в уже закалённом металле и в самых твёрдых сплавах. То же и со штампами. Обычно штамп закаляют уже после его тщательной отделки. На ультразвуковом станке сложнейшую обработку производит абразив (наждак, корундовый порошок) в поле ультразвуковой волны. Беспрерывно колеблясь в поле ультразвука, частицы твёрдого порошка врезаются в обрабатываемый сплав и вырезают отверстие такой же формы, как и у долота.Приготовление смесей с помощью ультразвука

Инфразвук— звуковые волны имеющие частоту ниже воспринимаемой человеческим ухом. Поскольку обычно человеческое ухо способно слышать звуки в диапазоне частот 16 - 20000 Гц, то за верхнюю границу частотного диапазона инфразвука обычно принимают 16 Гц. Нижняя же граница инфразвукового диапазона условно определена как 0,001 Гц. Практический интерес могут представлять колебания от десятых и даже сотых долей герц, то есть с периодами в десяток секунд.

Поскольку инфразвук слабо поглощается, он распространяется на большие расстояния и может служить предвестником бурь, ураганов, цунами. Для инфразвука характерно малое поглощение в различных средах вследствие чего инфразвуковые волны в воздухе, воде и в земной коре могут распространяться на очень далёкие расстояния. Это явление находит практическое применение при определении места сильных взрывов или положения стреляющего орудия. Распространение инфразвука на большие расстояния в море даёт возможность предсказания стихийного бедствия — цунами. Звуки взрывов, содержащие большое количество инфразвуковых частот, применяются для исследования верхних слоев атмосферы, свойств водной среды.

Сейсмические волны — волны энергии, которые путешествуют по земле или другим упругим телам в результате процесса, производящего низкочастотную акустическую энергию (землетрясение, взрыв и т. д.). Сейсмические волны изучаются сейсмологами и геофизиками. Их изучают при помощи сейсмографа, геофона, гидрофона или акселерометра.

Землетрясения создают разные типы сейсмических волн с разной скоростью. Волна фиксируется на ряде сейсмологических станций, и по разнице во времени учёные вычисляют эпицентр. В геофизике преломление или отражение сейсмических волн используется для изучения глубин Земли, искусственные волны используются для исследования подземных структур.

Типы сейсмических волн

Есть два главных типа: объёмные волны и поверхностные волны. Кроме описанных ниже есть и другие, менее значимые типы волн, которые вряд ли можно встретить на Земле, но они имеют важное значение в астросейсмологии.

Объёмные волны

Они проходят через недра Земли. Путь волн преломляется различной плотностью и жёсткостью подземных пород.

P-волны

P-волны (первичные волны) — продольные, или компрессионные волны. Обычно их скорость в два раза быстрее S-волн, проходить они могут через любые материалы. В воздухе они принимают форму звуковых волн, и, соответственно, их скорость становится равной скорости звука. Стандартная скорость P-волн — 330 м/с в воздухе, 1 450 м/с в воде и 5 000 м/с в граните.

S-волны

S-волны (вторичные волны) — поперечные волны. Они показывают, что земля смещается перпендикулярно к направлению распространения. В случае горизонтально поляризованных S-волн земля движется то в одну сторону, то в другую попеременно. Волны этого типа могут действовать только в твёрдых телах.

Поверхностные волны

Поверхностные волны несколько похожи на волны воды, но в отличие от них они путешествуют по земной поверхности. Их обычная скорость значительно ниже скорости волн тела. Из-за своей низкой частоты, времени действия и большой амплитуды они являются самыми разрушительными изо всех типов сейсмических волн. Они бывают двух типов: волны Рэлея и волны Лява.

P- и S-волны в мантии и ядре

Когда происходит землетрясение, сейсмографы вблизи эпицентра записывают S- и P-волны. Но на больших расстояниях обнаружить высокие частоты первой S-волны невозможно. Поскольку поперечные волны не могут проходить через жидкости, на основании этого явления Ричард Диксон Олдхэм выдвинул предположение, что Земля имеет жидкое внешнее ядро. По этому виду исследования в дальнейшем было выдвинуто предположение, что у Луны твёрдое ядро, но недавние геодезические исследования показывают, что оно ещё расплавлено.

Использование P- и S- волн для локации землетрясения

В случае локальных или близлежащих землетрясений разница прибытия P- и S- волн может использоваться для обнаружения дистанции от события. В случае глобальных землетрясений четыре или более наблюдательных станций, синхронизированных по времени, записывают время прибытия P-волн. На основе этих данных можно вычислить эпицентр в любой точке планеты. Для определения гипоцентра используется больший объем данных (десятки или сотни записей прибытия P-волн с сейсмических станций).

Самый простой способ узнать место землетрясения в радиусе 200 км — это высчитать разницу в прибытии P- и S- волн в секундах и умножить ее на 8. Но на телесейсмических дистанциях этот способ не подходит потому, что высока вероятность того, что сейсмические волны углубились до мантии Земли и преломились, изменив свою скорость.

Билет 13.Деформация тел.Типы и параметры деформаций.Закон Гука.Энергия упругой деформации.

1)Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия(другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.

2)Виды деформацииНаиболее простые виды деформации тела в целом:растяжение-сжатие,(возникает в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс)). сдвиг,( возникает в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно))изгиб, кручение.

В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу

3)Закон Гука Для тонкого растяжимого стержня закон Гука имеет вид:

З десь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины  ) явно, записав коэффициент упругости как

Величина   называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Е сли ввести относительное удлинение и нормальное напряжение в поперечном сечении,то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

С ледует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

4) Энергия упругой деформации

Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины.

Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения.Сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.

Среднее значение силы равно F_ср=kl . Для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:

A=1/2 kl•l=1/2kl².

Таким образом, потенциальная энергия упругости Е_п равна

E_п = 1/2 kl².          (98.1)

З десь потенциальная энергия выражена через коэффициент упругости пружины и через наибольшее растяжение ее. Полученное выражение для потенциальной энергии можно записать и иначе, через величину силы упругости при наибольшем растяжении и коэффициент упругости:    

Хрупкость — свойство материала разрушаться без образования заметных остаточных деформаций. Является противоположным свойству пластичности. Материалы, обладающие этим свойством, называются хрупкими. Для таких материалов удлинение при разрыве не превышает 2…5 %, а в ряде случаев измеряется долями процента. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, стекло, кирпич, камни и др.

Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость нагружения и температура. При быстром нагружении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства. При понижении температуры хрупкость материалов увеличивается, а при повышении температуры увеличивается свойство пластичности.

Одной из основных технологических операций, позволяющих изменять в нужном направлении свойства материала, является термообработка. Закалка резко повышает прочностные характеристики стали и одновременно снижает ее пластические свойства.

Пласти́чность — способность материала без разрушения получать большие остаточные деформации. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, изгиб и др. Мерой пластичности являются относительное удлинение δ и относительное сужение ψ, определяемые при проведении испытаний на растяжение. Чем больше δ, тем более пластичным считается материал. По уровню относительного сужения ψ можно делать вывод о технологичности материала. К числу весьма пластичных материалов относятся отожженная медь, алюминий, латунь, золото, малоуглеродистая сталь и др. Менее пластичными являются дюраль и бронза. К числу слабо пластичных материалов относятся многие легированные стали.

Деление материалов на пластичные и хрупкие является условным не только потому, что между теми и другими не существует резкого перехода в значениях δ и ψ. В зависимости от условий испытания многие хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие.

Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость натяжения и температура. При быстром натяжении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства

Упругой деформацией называется та деформация, при которой после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определённого значения, которое называется пределом упругости. При повышении этого предела деформация становится пластической. В этом случае после устранения внешних сил первоначальная форма и размеры тела полностью не восстанавливаются.

Тектоническими движениями называются перемещения вещества земной коры под влиянием процессов, происходящих в более глубоких недрах Земли. Эти движения вызывают тектонические нарушения, т. е. изменения первичного залегания горных пород. Особенно отчетливо эти изменения наблюдаются на примере осадочных пород, которые первично отлагаются в виде горизонтально залегающих пластов, а вследствие тектонических нарушений оказываются смятыми в складки или разорванными на отдельные чешуи и блоки. Тектонические движения, в конечном счете создают наблюдаемую структуру земной коры, т. е. они являются созидательными движениями («тектонос» по-гречески— созидательный). В результате этих движений возникают и основные неровности рельефа поверхности Земли.

БИЛЕТ 14

 Кинематическое описание движения жидкости и газа − гидрокинематика. Поле скоростей, линии и nрубки тока. Закон (ур-ние) Бернулли и его следствие. Внутренние трение, течение вязкой жидкости. Понятие о реологии. Ламинарные и турбулентные потоки. Число Рейнольдса. Подъёмная сила и лобовое сопротивление.

Гидродинамика - раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей и взаимодействие несжимаемых жидкостей с твёрдыми телами. Рассмотрим движение несжимаемой жидкости. Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости  , как функцию времени  .Совокупность векторов , заданных для всех точек пространства, образует так называемое поле вектора скорости .

При кинематическом описании движения любой механической системы нет необходимости подробно рассматривать внутренние физические свойства тел, включенных в систему.При описании движения жидкости достаточно принять во внимание ее текучесть − способность изменять свою форму при малейшем внешнем воздействии. Свойства жидкостей и газов существенно различаются, однако описание движения жидкостей и газов сходно,  описание движения газов проводится аналогично описанию движению жидкости. Мы будем следить не за отдельной частицей жидкости (ее скоростью, траекторией и другими характеристиками), а за скоростью жидкости в данной пространственной точке, не обращая внимания, что в другой момент времени в рассматриваемой точке будет находиться другая частица жидкости. Таким образом, основной характеристикой движения будем считать пространственное распределение скоростей жидкости, которое задается векторной функцией V(t, х, у, z) − функцией, задающей вектор скорости жидкости в любой точке, в любой момент времени. Четырем числам (трем координатам и времени) ставится в соответствие три числа (компоненты вектора).

Введенная функция V(t, х, у, z)  называется полем скоростей(Поле скоростей - это совокупность векторов V(t), заданных для всех точек пространства). Часто распределение скоростей может сохраняться в течение некоторого промежутка времени − тогда функция V(t, х, у, z) = V(х, у, z) не зависит от времени. Такое поле скоростей называется стационарным. Если же скорости движения жидкости одинаковы во всех точках, то поле скоростей называется однородным. Подчеркнем, стационарное − значит, в рассматриваемом временном промежутке скорости остаются постоянными (но могут быть различными в разных точках); однородное − значит, в рассматриваемом объеме скорости одинаковы во всех пространственных точках (но могут изменяться с течением времени).

Наглядно представить себе векторное поле достаточно затруднительно − в каждой точке необходимо изобразить вектор, что, конечно, невозможно. Поэтому используются несколько упрощенных способов графического представления векторных полей. Наиболее часто встречается изображение векторных с помощью линий поля − линий, касательные к которым совпадают с вектором поля (см. рис. 175).

В рассматриваемом случае поля скоростей − линии поля называются линиями тока. Линия тока − такая линия, касательная к которой в каждой точке совпадает с направлением вектора скорости в данной точке. На линиях тока принято указывать направление движения жидкости. Заметим, что линию тока можно провести через любую точку, поэтому число линий, их густота определяются исключительно эстетическими соображениями.  Семейство линий тока достаточно наглядно представляет движение жидкости в некоторой области (рис. 176).

Исходя из определения, можно установить их общие свойства:  1. Линии тока не пересекаются (в противном случае в точке пересечения можно построить двекасательные, то есть в одной точке скорость жидкости имеет два значения, что абсурдно).  2. Линии тока не имеют изломов (в точке излома опять можно построить две касательные).  3. Линии тока начинаются на источниках и заканчиваются на точках стока жидкости.  Если движение жидкости является стационарным, то линии тока совпадают с траекториями движения частиц жидкости. В нестационарном потоке линии тока изменяются с течением времени, поэтому траектория отдельно взятой частицы отличается от линии тока. В этом случае линии тока следует рассматривать как вспомогательные математические иллюстрации, не имеющие явного физического смысла.

Трубка тока – это часть жидкости, ограниченная линиями тока. Частицы жидкости при своём движении не пересекают стенок трубки тока.

Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение S за время Dt, равен SvDt.

р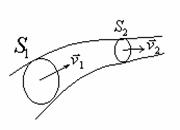 ис.1

Тогда Q = Sv  - поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечение S за единицу времени.

Если жидкость несжимаема, то объем жидкости между сечениями S1 и S2 будет оставаться неизменным, и тогда S1v1 = S2v2 . Это справедливо для любой пары S1 и S2 , и мы получаем

 Sv = const – теорема о неразрывности струи:

 Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

 — плотность жидкости,

 — скорость потока,  — высота, на которой находится рассматриваемый элемент жидкости,  — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости.

g— ускорение свободного падения.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической ипотенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давленияи не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Соотношение, близкое к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы   и уравнение Бернулли принимает вид:    .

Давление меньше в тех точках, где скорость больше.

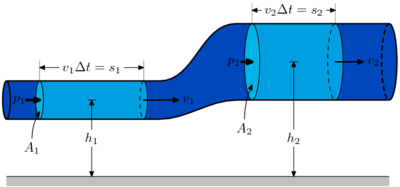
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового  , статического   и динамического   давлений.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, но выполняется для реальных жидкостей, у которых внутреннее трение невелико. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Практические следствия:

• закон Бернулли объясняет эффект притяжения между телами, находящимися вблизи границ потоков движущихся жидкостей (газов). Иногда это притяжение может создавать угрозу безопасности. Например, при движении скоростного поезда «Сапсан» (скорость движения более 200 км/час) для людей на платформах возникает опасность сброса под поезд.[9]Аналогично «затягивающая сила» возникает при движении судов параллельным курсом: например, подобные инциденты происходили с лайнером «Олимпик».

• Автоаварии: проносящиеся мимо многотонные грузовики с прицепами притягиваются к стоящему на обочине автобана автомобилю. Это одна из опасностей, которыми объясняют запрет на остановку автомобилей на обочинах автобанов.

Вязкость (внутреннее трение) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения.

До сих пор полагали, что скорость движения одинакова на сечении трубки. Реально из-за вязкости скорость течения жидкости различна у стенок и вдали от них.Сила взаимодействия соседних слоев, соприкасающихся по поверхности S, равна: F=ƞ*(dV/dX)*S, где ƞ- коэффициент вязкости, измеряется в Пуазах, 1Па*с=10 Пз. Ƞ показывает насколько быстро передается импульс из одного слоя в другой.dV/dX – производная, показывающая, как быстро изменяется в данном месте скорость течения.

Ламинарное течение - (lamina-пластинка,полоска) течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Ламинарное течение является стационарным.

При ламинарном течении жидкости в круглой трубе V=0 у стенки и максимальна на оси трубы.

V(r)=V₀ (1-r²/R²). При ламинарном течении скорость изменяется с расстоянием от оси трубы по параболическому закону.

Q= –формула Пуазейля, определяет вязкость жидкостей и газов.Q-поток жидкости(объем жидкости, протекающий через поперечное сечение трубы в единицу времени). l-длина трубы.

Реология- раздел физики, изучающий деформации и текучесть вещества. Изучая деформационные свойства реальных тел реология занимает промежуточное положение между теорией упругости и гидродинамикой.Ламинарный поток – это такой вид потока, в котором частицы сохраняют постоянное равномерное движение по параллельным траекториям. Этот тип потока существует, например, в прямых круглых трубах или между параллельными стенками при низких скоростях.

С другой стороны, в турбулентном потоке частицы обладают хаотическим движением и интенсивно перемешиваются друг с другом.

Длина линии представляет собой среднюю скорость частиц в различных точках сечения вдоль траектории, как показано на рис. 7.8. В ламинарном потоке скорость максимальна в центре потока. Вследствие трения между слоями скорость постепенно замедляется по направлению к стенкам, где она равна нулю.

В турбулентном потоке слои перемешиваются и, следовательно, скорость жидкости примерно одинакова в центральной части потока, но быстро падает по направлению к стенкам. У стенок очень тонкий ламинарный поток жидкости имеет нулевую мгновенную скорость.

Для получения ламинарного потока в круглой трубе ее диаметр должен быть мал, скорость низка, а вязкость жидкости высока.

Число Рейнольдса (Re). Re= ,где þ – плотность,v–ср по сечению трубки скорость потока, ƞ – вязкость жидкости, l – размер потока, характерный для поперечного сечения. При малых значения Re течение носит ламинарный характер, начиная с критического значения Re, течение приобретает турбулентный характер. (Если l- радиус трубы, то Re_кр=1000, если l-диаметр трубы,то Re_кр=2000).ʋ= , ʋ - кинематическая вязкость, ƞ- динамическая вязкость. Re= .

Силу, с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скорости v невозмущенного потока силу X, называемую лобовым сопротивлением, и перпендикулярную к v силу Y, называемую подъемной силой. Лобовое сопротивление слагается из сил давления и сил внутреннего трения.

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах.

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. Подъемная сила равна нулю для симметричных тел.

При малых значения Reмодуль силы сопротивления определяется формулой:F=kƞlv.(ƞ – динамическая вязкость, v – скорость тела, l – размер,k – коэффициент пропорциональности, который зависит от формы тела).

15. МКТ вещества. Состояние вещества и термодинамические параметры его определяющие. Характеристики атомов и молекул и экспериментальные методы их определения. Кинетическая теория изучает свойства веществ, рассматривая их состоящими из атомов, которые находятся в непрерывном хаотическом движении. Огромное число отдельных объектов (атомов и молекул) делает невозможным описание их состояния с точки зрения законов Ньютона. Поэтому в молекулярной физике используется статистический метод, когда для характеристики того или иного параметра вещества используются усредненные значения.

Первым объектом нашего изучения явится газообразное состояние вещества. В основе кинетической теории газов лежат следующие постулаты: 1. все тела состоят из большого количества атомов и молекул, движущихся в случайных направлениях с различными скоростями 2. расстояния между молекулами значительно превышают размеры самих атомов или молекул 3. каждая из молекул подчиняется законам классической механики, но их кинетическая энергия много больше, чем потенциальная энергия взаимодействия между собой 4. взаимодействие молекул носит характер упругих столкновений.

Газ, который удовлетворяет всем этим требованиям - идеальный. Это абстрактная модель, в действительности поведение реальных газов только приближенно следует закономерностям, полученным для идеального. Степень приближения связана прежде всего с конечными размерами реальных молекул, тогда как в модели идеального газа их принято считать материальными точками. Справедливости ради необходимо отметить, что в нормальных условиях поведение большинства реальных газов может достаточно точно описываться законами идеального газа, но при сильных сжатиях конечный размер молекул приводит к заметному отклонению поведения реальных газов от идеального.

Описание состояния идеального газа. Для однозначного определения положения в пространстве одной молекулы идеального газа необходимо знать ее три координаты. Число молекул в одном кубическом сантиметре примерно 2,7*10¹⁹. Поэтому даже современный компьютер не в состоянии решить соответствующую систему уравнений. Задача молекулярной физики состоит в том, чтобы попытаться описать состояние газа с помощью небольшого количества физических параметров (давления, температуры, массы, теплоемкости), связав их со свойствами отдельных атомов и молекул. Решение этой задачи достигается путем усреднения отдельных микроскопических величин. Такое усреднение может быть проведено различными способами.

Пусть, например, требуется найти среднее число молекул в определенном объеме. Его можно найти, либо вычисляя среднее число в заданном объеме в различные моменты времени, либо беря различные одинаковые объемы в различных частях сосуда, содержащего идеальный газ. Обозначим среднее значение числа молекул, найденное по первому способу как N_t , а среднее по второму-N_анс. Первое из них обычно называют средним по времени, а второе - средним по ансамблю - совокупность отдельных воображаемых величин. В настоящее время считается, что N_t=N_анс. Доказательства справедливости этого равенства до сих пор не существует, и его принимают как некоторую гипотезу. Величины, найденные таким способом макроскопические. Если значения макроскопического параметра оказывается одинаковыми для любых выбранных частей рассматриваемой системы и не изменяются с течением времени, то говорят о равновесном значении этого параметра. Если в системе установилось равновесие по всем параметрам, характеризующим систему, то такая система - равновесная.

При этом отдельные макроскопические величины оказываются связанными друг с другом. Так, например, опытным путем были установлены газовые законы: Шарля р/T = const, Гей-Люссака V/T = const, Бойля - Мариотта pV = const, а также объединенный закон Менделеева - КлапейронаpV=(m/)RT, связывающие макроскопические величины m, молекулярного веса , р, V и Т. Из этих законов видно, что изменение одного параметра вызывает изменение другого. Ясно, что любое изменение параметра влечет нарушение равновесного состояния системы. Поэтому для того, чтобы в любой момент времени система находилась в равновесном состоянии, требуются бесконечно малые изменения параметров, и переход из одного равновесного состояния в другое должен происходить бесконечно долго. В реальной жизни рассматриваются квазиравновесные процессы, происходящие достаточно медленно и долго.

Основное уравнение кинетической теории. Предполагается, что давление газа на стенку сосуда создается за счет упругих ударов молекул газа об эту стенку. При упругом ударе сохраняется кинетическая энергия молекул, и, следовательно, скорость молекулы до и после

Выберем некоторый участок поверхности стенки площадью S и подсчитаем количество ударяющихся о стенку в единицу времени молекул, скорости которых имеют проекцию на ось Х, близкую к значению . Пусть концентрация таких молекул равна n_i. Массы всех молекул считаются одинаковыми и равными m.

Если до удара о стенку проекция импульса на ось Х была , то после удара она станет (- ). Изменение импульса молекулы, а, следовательно, и изменение импульса стенки k_i равно: k_i = - (- ) = 2 . (11-1)

Из выделенной группы молекул за промежуток времени dt достигнут поверхности S лишь те молекулы, скорости которых направлены к стенке ( ), и которые находятся от стенки не далее расстояния l= dt . Другими словами, те молекулы, которые находятся внутри объема V=S dt. Как уже отмечалось, n_i, поэтому общее число их ударов о стенку за время dt равно N_i=n_iS dt. В результате ударов этих молекул импульс стенки изменится на величину

К_i=2 N_i=2 n_iS dt=2mn_iS dt. (11-2)

Чтобы найти общее изменение импульса всех молекул при ударах о стенкуК, нужно просуммировать выражение (11-2) по всем значениям скоростей молекул, т.е. по всем : К = Умножая и деля правую часть на концентрацию молекул n, рассмотрим величину суммы , (11-4) k₁ ,k₂ ,..k_i,...k_N - количество появления тех или иных значений скорости. Из статистики известно, что сумма (11-4) - среднее арифметическое (среднее значение величины ), числа k₁,k₂,....k_i,...k_N характеризуют так называемые статистические веса значений v₁ ,v ₂ , ..v_i, ... v_N. С учетом определения (11-4) выражение (11-3) принимает следующий вид: К=2mSn dt. (11-5)

Среднеквадратичную проекцию скорости молекул на ось Х можно связать со среднеквадратичной скоростью хаотического движения молекул в предположении о равноправии всех трех осей координат. Т.к. v²= , и все направления скорости равновероятны, можно считать .Учтем, что движение в сторону положительных и отрицательных значений х также равновероятны, поэтому = . Деля обе части (11-5) на t и замечая по 2 закону Ньютона представляет силу, действующую на стенку: . Поскольку сила, деленная на площадь - давление на единицу площади, то (11-5): , (11-6) основное уравнение кинетической теории газов. Величину давления можно выразить через среднюю энергию, приходящуюся на одну молекулу. = , (11-7)

БИЛЕТ 17

Распределение Максвелла – распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, при условии, что 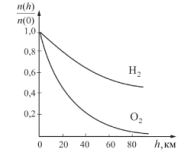движение частиц подчиняется законам классической механики. Установлено Дж. Максвеллом в 1859 году.

Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение, при этом на газ не действуют силовые поля.

(функция распределения Максвелла)

f(V) зависит от рода газа (массы частицы) и температуры, не зависит от характера взаимодействия частиц и от внешних сил. Также распределение Максвелла можно применять не только для газов, но и для жидкостей.

Наиболее вероятная скорость:

Средняя скорость:

Средняя квадратичная скорость:

Экспериментальное значение.

Распределение молекул по скоростям исследовал экспериментально различными методами. Рассмотрим идею метода Ламмерта. Пучок молекул, выходящий из отверстия в сосуде, стенки которого поддерживались при заданной температуре, проходил через щель в первом диске. Через щель во втором диске могли пройти лишь те молекулы, которые долетали до него в тот момента, когда на их пути оказывалась щель в этом диске. Более медленные молекулы достигнут второго диска слишком поздно, а более быстрые – слишком рано, для того, чтобы пройти через щель. Следовательно, такое устройство (называемое селектором скоростей) выделяет из пучка молекулы, обладающие скоростями, заключёнными в узком интервале (ширина интервала определялась шириной щели).

Если диски вращаются с угловой скоростью ω, то они повернутся на угол φ между щелями за время t = φ/ω. За это время достигнут второго диска и, следовательно, пройдут через его щель молекулы, скорость которых v = l/t = lω/φ. Это и есть средняя скорость молекул, прошедших через селектор. Изменяя корость вращения дисков, можно было выделять из пучка молекулы, обладающие скоростями в различных интервалах Δv. Улавливая эти молекулы в течении некоторого времени, можно было определять их относительное количество. Надо иметь ввиду, что распределение по скоростям молекул, вышедших через отверстие в сосуде (т.е. молекул в пучке), отличается от распределения в закрытом сосуде. Это обусловлено тем, что более быстрые молекулы выходят из отверстия в относительно большем количестве, чем более медленные, в результате чего пучок оказывается обогащённым более быстрыми молекулами. Учёт этого обстоятельства приводит к следующей функции распределения скорости в пучке:

Результаты всех экспериментов, осуществлённых различными методами, оказались в полном согласии с распределением, полученным теоретически Максвеллом.

БИЛЕТ 18

Распределение Больцмана.

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T=0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности.

При высоких температурах наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh–это потенциальная энергия U, то на разных высотах U=mghразлично. Следовательно, характеризует распределение частиц по значениям потенциальной энергии

Барометрический закон.

Атмосферное давление на какой-либо высоте h обусловлено весом слоёв аза, лежащих выше. Пусть P –давление на высоте h, а P + dP–на высоте h + dh. Причём, dh>0, dP<0, так как на большой высоте давление меньше. Разность давления P – (P + dP)равна весу газа, заключённого в объёме цилиндра с площадью основания равного 1 и высотой dhт.к.

Барометрической формулой можно рассчитать давление или число частиц на определённой высоте в атмосфере.

Уравнение идеального газа.

Параметры состояния равномерно связаны друг с другом. Соотношение, определяющее связь между параметрами состояния какого-либо тела, называется уравнением состояния этого тела.

В простейшем случае равновесное состояние тела определяется значениями трёх параметров: давления, объёма и температуры (масса тела предполагается известной).

Опытным путём было установлено, что при обычных условиях (т.е. при комнатной температуре и атмосферном давлении) параметры состояния таких газов, как кислород и азот, довольно хорошо подчиняются уравнению:

Оказалось также, что чем разрежённее газ (чем меньше его плотность), тем точнее выполняется это уравнение. У разрежённых газов молекулы практически не взаимодействуют между собой. Они лишь иногда сталкиваются друг с другом. Однако эти столкновения происходят настолько редко, что большую часть времени молекулы движутся свободно. Идеальный газ – газ, взаимодействием которого между молекулами можно пренебречь. Особенно близки по своим свойствам к идеальному газе гелий и водород.

Согласно закону Авогадро при нормальных условияхобъём любого газа равен . Отсюда следует, что в случае, когда количество газа равно одному молю, константа bбудет одинаковой для всех газов. Обозначив константу bдля одного моля буквой R, напишем уравнение состояния идеального газа следующим образом:

Индекс «м» указывает на то, что имеется ввиду молярный объём.

Константа R называется молярной газовой постоянной или просто газовой постоянной.

Чтобы получить уравнение состояния для произвольной массы mидеального газа, умножим обе части уравнения на отношение m/M, где M–молярная масса газа:

Явления переноса.

Диффузия – обусловленное тепловым движением выравнивание концентраций в смеси нескольких веществ, процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму. Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения.

Теплопроводность - это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Внутреннее трение (вязкость) - одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость измеряется в килограммах на метр-секунду (кг/(м*с)) или, что то же самое, в паскаль-секундах (Па * с).

№19

Первое начало термодинамики. Внутренняя энергия. Теплота и работа. Число степеней свободы атомов и молекул.. Закон распределения энергии по степеням свободы. Теплоемкость идеального газа при постоянном объёме и давлении. Работа идеального газа при различных процессах.

Внутреннее изменение внутренней энергии происходит по средствам механического воздействие и теплопередачи. Теплопередача делится на теплопроводность, конвенция и излучение.

Внутренняя энергия слагается из кинетической энергии поступательного и вращательного движения молекул, кинетической и потенциальной энергии колебательного движения атомов в молекулах, потенциальной энергии взаимодействия между молекулами и внутримолекулярной энергии.

изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: где — подведённое к телу количество теплоты, измеренное в джоулях ^[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение: гдеT — температура, измеренная в кельвинахS— энтропия, измеренная в джоулях/кельвин; P — давление, измеренное в паскалях  — химический потенциал  — количество частиц в системе

Внутренняя энергия U является функцией состояния системы

Обмен механической энергией характеризуется совершенной работой А, а обмен внутренней энергией – количеством переданного тепла Q.

Превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. В этом и состоит суть первого начала термодинамики, следующего из закона сохранения энергии.

Количество теплоты Q – изменение внутренней энергии тела, которое произошло в результате теплообмена. Тепловой поток всегда направлен от горячего к холодному.

    Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: – это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике.

   Правило знаков:   если тепло передаётся от окружающей среды данной системе,   и   если система производит работу над окружающими телами, при этом  . Учитывая правило знаков, первое начало термодинамики можно записать в виде:

,

– изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы.

    Выражение (4.1.1) для малого изменения состояния системы будет иметь вид:

В этом выражении U – функция состояния системы; dU – её полный дифференциал, а δQ и δА таковыми не являются. В каждом состоянии система обладает определенным и только таким значением внутренней энергии, поэтому можно записать:

Важно отметить, что теплота Q и работа А зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорически, адиабатически и т.д.), а внутренняя энергия U не зависит. При этом нельзя сказать, что система обладает определенным для данного состояния значением теплоты и работы.

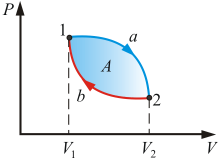Из формулы (4.1.2) следует, что количество теплоты выражается в тех же единицах, что работа и энергия, т.е. в джоулях (Дж)

   Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний, возвращается в исходное. На рисунке 4.1 изображен циклический процесс 1–а–2–б–1, при этом была совершена работа А.

Так как U – функция состояния, то

  Это справедливо для любой функции состояния.

 Если   то согласно первому началу термодинамики  , т.е. нельзя построить периодически действующий двигатель, который совершал бы бóльшую работу, чем количество сообщенной ему извне энергии. Иными словами, вечный двигатель первого рода невозможен. Это одна из формулировок первого начала термодинамики. Следует отметить, что первое начало термодинамики не указывает, в каком направлении идут процессы изменения состояния, что является одним из его недостатков. Механическая работа определяется как: ,где   — сила, а   — элементарное (бесконечно малое) перемещение.Элементарная работа термодинамической системы над внешней средой может быть вычислена так: ,где   — нормаль элементарной (бесконечно малой) площадки,   — давление и   — бесконечно малое приращение объёма.Работа в термодинамическом процессе  , таким образом, выражается так: .

Величина работы зависит от пути, по которому термодинамическая система переходит из состояния 1 в состояние 2, и не является функцией состояния системы. Такие величины называют функциями процесса.

 Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус: Размерность теплоемкости: [C] = Дж/К.

       Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.        Удельная теплоёмкость (С_уд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C_уд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:        [Cμ] = Дж/(моль×К).

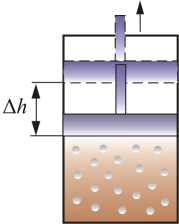      Из п. 1.2 известно, что молярная масса – масса одного моля: где А – атомная масса; m_ед - атомная единица массы; N_А - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода ¹²С/    Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.   Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С_V.– теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).       Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что  .Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния. Величины С_Р и С_V оказываются связанными простыми соотношениями. Найдём их. Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде: т.е. бесконечно малое приращение количества теплоты   равно приращению внутренней энергии dU. Теплоемкость при постоянном объёме будет равна:        В общем случае        так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4). , ,

      Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.   Для произвольной идеальной массы газа:        При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:

.

.

       Из основного уравнения молекулярно-кинетической теории . При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:

      Это уравнение Майера для одного моля газа.     Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

       Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей:    или

 Молекулы многоатомных газов нельзя рассматривать как материальные точки. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул.         Числом степени свободы (i) называется минимальноечисло независимых переменных, определяющих полное положение тела в пространстве.         Положение одноатомной молекулы, как и материальной точки, задаётся тремя координатами, поэтому она имеет три степени свободы (рис. 4.3).

  Рис. 4.3

       Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения, а любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомной молекулы вращение вокруг её собственной оси не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю (рис. 4.3).         Таким образом, у двухатомных молекул пять степеней свободы (i = 5), а у трёхатомных шесть степеней свободы (i = 6).

       При взаимных столкновениях молекул возможен обмен их энергиями и превращение энергии вращательного движения в энергию поступательного движения и обратно. Таким путём было установлено равновесие между значениями средних энергий поступательного и вращательного движения молекул. Больцман доказал, что для не слишком низких температур средняя энергия  , приходящаяся на одну степень свободы, равна 

Закон о равномерном распределении энергии по степеням свободы: Если система молекул находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой из них она равно 1/2kT.

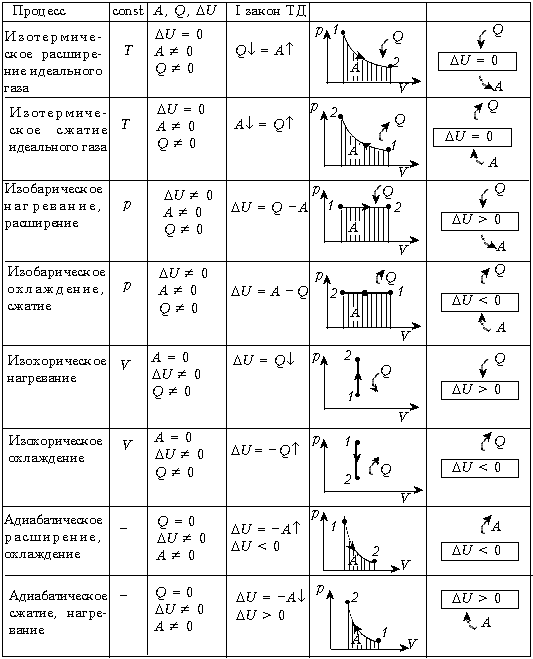       Здесь уместно рассмотреть еще и политропический процесс – такой процесс, при котором изменяются все основные параметры системы, кроме теплоемкости, т.е. С = const.         Уравнение политропы: или

Здесь n – показатель политропы.         С помощью этого показателя можно легко описать любой изопроцесс.         1. Изобарический процесс Р = const, n = 0:

       2. Изотермический процесс Т = const, n = 1,           3. Изохорический процесс V = const,  :

       4. Адиабатический процесс ΔQ = 0, n = γ, С_ад = 0. Во всех этих процессах работу можно вычислить по формуле:

.

№20

Второе начало термодинамики. Обратимые и необратимые процессы. Энтропия и ее вязь с вероятностью состояния. Циклические процессы. Тепловые машины и холодильники. Цикл Карно и КПД тепловых машин. Термодинамические потенциалы. Границы применимости второго начала термодинамикиП режде чем переходить к изложению второго закона термодинамики, рассмотрим круговые процессы. Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние. В диаграммах состояния P, V и других круговые процессы изображается в виде замкнутых кривых (рис. 5.1). Это связано с тем, что в любой диаграмме два тождественных состояния (начало и конец кругового процесса) изображаются одной и той же точкой на плоскости.

       Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – 2) и сжатия (2 – 1) газа. Работа расширения (определяется площадью фигуры 1a2V₂V₁1) положительна ( ), работа сжатия (определяется площадью фигуры 2b1V₁V₂2) отрицательна (dV< 0). Следовательно, работа, совершаемая за цикл, определяется площадью, охваченной замкнутой кривой. Если за цикл совершается положительная работа

(цикл протекает по часовой стрелке), то он называется прямым (рис. 5.1). Если за цикл совершается отрицательная работа (цикл протекает против часовой стрелки), то он называется обратным (рис. 5.2).Круговые процессы лежат в основе всех тепловых машин: двигателей внутреннего сгорания, паровых и газовых турбин, паровых и холодильных машин и т. д. В результате кругового процесса система возвращается в исходное состояние, и следовательно полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики для кругового процесса

т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому где Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой.  Поэтому термический коэффициент полезного действия для кругового процесса   Все термодинамические процессы, в том числе и круговые, делят на две группы: обратимые и необратимые. Процесс называют обратимым, если он протекает таким образом, что после окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что и прямой процесс. После проведения кругового обратимого процесса никаких изменений в среде, окружающей систему, не произойдет. При этом под средой понимается совокупность всех не входящих в систему тел, с которыми система непосредственно взаимодействует.  Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния. Нельзя осуществить необратимый круговой процесс, чтобы нигде в окружающей среде не осталось никаких изменений. Свойством обратимости обладают только равновесные процессы. Каждое промежуточное состояние является состоянием термодинамического равновесия, нечувствительного к тому, идет ли процесс в прямом или обратном направлении. Например, обратимым можно считать процесс адиабатического расширения или сжатия газа. При адиабатическом процессе условие теплоизолированности системы исключает непосредственный теплообмен между системой и средой. Поэтому, производя адиабатическое расширение газа, а затем сжатие, можно вернуть газ в исходное состояние так, что в окружающей среде никаких изменений не произойдет. Конечно, в реальных условиях, и в этом случае, всегда имеется некоторая необратимость процесса, обусловленная, например, несовершенством теплоизоляции, трением при движении поршня и т.д. Только в обратимых процессах теплота используется по назначению, не расходуется зря. Если процесс неравновесный, то будет необратимый переход, т.е. часть энергии уйдет (необратимо).

       Максимальным КПД обладают машины, у которых только обратимые процессы. Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.), которая нами не рассматривается.Обратимые процессы – это в какой-то степени идеализация реальных процессов. Их рассмотрение важно по двум причинам:многие процессы в природе и технике практически обратимы;обратимые процессы являются наиболее экономичными и приводят к максимальному значению термического коэффициента полезного действия тепловых двигателей.

  Тепловой машиной называется периодический действующий двигатель, совершающий работу за счет получаемого извне тепла. Любая тепловая машина работает по принципу кругового (циклического) процесса, т.е. возвращается в исходное состояние (рис. 5.1). Но чтобы при этом была совершена полезная работа, возврат должен быть произведен с наименьшими затратами.Полезная работа равна разности работ расширения и сжатия, т.е. равна площади, ограниченной замкнутой кривой. Обязательными частями тепловой машины являются нагреватель (источник энергии), холодильник, рабочее тело (газ, пар). Зачем холодильник? Так как в тепловой машине реализуется круговой процесс, то вернуться в исходное состояние можно с меньшими затратами, если отдать часть тепла. Или если охладить пар, то его легче сжать, следовательно работа сжатия будет меньше работы расширения. Поэтому в тепловых машинах используется холодильник.

       Прямой цикл используется в тепловом двигателе – периодически действующей тепловой машине, совершающей работу за счет полученной извне теплоты. Рассмотрим схему теплового двигателя (рис. 5.3). От термостата с более высокой температурой Т₁, называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой Т₂, называемому холодильником, за цикл передается количество теплоты Q₂ и совершается работа A:

Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. Принцип действия холодильной машины представлен на рисунке 5.4. Системой за цикл поглощается при низкой температуре T₂ количество теплоты Q₂ и отдается при более высокой температуре Т₁ количество теплоты Q₁ за счет работы внешних сил А.

К арно вывел теорему, носящую теперь его имя: Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников, наибольшим КПД обладают обратимые машины. Причем КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машины и от природы рабочего вещества. При этом КПД меньше единицы. Цикл, изученный Карно, является самым экономичным и представляет собой круговой процесс, состоящий из двух изотерм и двух адиабат (рис. 5.5). Рассмотрим круговой процесс, при котором тепло можно превратить в работу, притом наилучшим образом, т.е. чтобы работа была максимальна. Напомню, что тепловой машиной называется периодически действующий двигатель, совершающий работу за счет получаемого извне тепла и имеющего нагреватель, холодильник и рабочее тело. Так вот будем считать, что нагреватель и холодильник имеют бесконечную теплоемкость, т.е. их температуры не изменяются в процессе передачи тепла.  Рассмотрим процесс сначала качественно. Начнем процесс из т. А. Газ сжат до давления Р₀ и находится в контакте с нагревателем при Т₁. Расширение газа при каком процессе даст максимальную работу? Вспомним закон сохранения энергии в термодинамике, или I начало: В изотермическом процессе dU = 0, значит все тепло перейдет в работу: Итак, на участке АВ – изотермическое расширение при температуре Т₁ (процесс теплопередачи не происходит, т.к. нет разности температур, не происходит и передача тепла без совершения работы, т.е. процесс обратимый). Полученное рабочим телом тепло нужно передать холодильнику. Но если просто привести к соприкосновению с холодильником, то будет передача тепла без совершения работы. Поэтому нужно сначала рабочее тело охладить до Т₂ (а охлаждать без затрат тепла – это адиабатическое расширение участок ВС), а затем уже присоединять к холодильнику. Адиабатическим расширением заканчивается первая половина цикла –совершение полезной работы. Теперь необходимо вернуть рабочее тело в исходное состояние, т.е. сжать газ до Р₀. Контакт с нагревателем опять не следует делать, пока рабочее тело не примет температуру нагревателя (Т₁). Возвращение в т. А опять происходит в два этапа: сначала рабочее тело сжимают, не прерывая контакта с холодильником, при этом холодильнику отдается тепло Q₂ (изотермическое сжатие СD). Затем изолируют тело от холодильника, адиабатно сжимают его, при этом температура его повышается до Т₁ (DА). Рабочее тело при адиабатическом сжатии нагревается за счет внешней работы, совершаемой над ним. Как видим, на всех стадиях кругового процесса нигде не допускается соприкосновение тел с разной температурой, т.е. нет необратимых процессов теплопроводности. Весь цикл проводится обратимо (бесконечно медленно).Найдем полезную работу цикла Карно. Процесс А–В. Положительная работа, совершенная газом при изотермическом расширении одного моля газа от V₀ до V₁. Тепло, полученное от нагревателя Q₁, идет на изотермическое расширение газа, совершая при этом работу А₁:

Процесс В–С – адиабатическое расширение. При адиабатическом расширении теплообмен с окружающей средой отсутствует и работа расширения А₂ совершается за счет изменения внутренней энергии. Уравнение адиабаты     Давление при этом изменится до Р₂. Полученная работа на этой стадии:

       Процесс С–D – изотермическое сжатие. На третьем этапе газ изотермический сжимается V₂ до V₃. Теплота Q₂, отданная газом холодильнику при изотермическом сжатии, равна работе сжатия А₃ – это работа совершаемая над газом, она отрицательна: Процесс D–А – адиабатическое сжати е.

Уравнение адиабаты: 

  Работа сжатия на последнем этапе: Общая работа цикла A = A₁ + A₂ + A₃ + A₄, или Обозначим 

  , тогда

       Значит работа, совершаемая газом больше работы внешних сил. Работа равна площади ограниченной кривой АВСDА.   Из равенств следует:

       Полезная работа:

       КПД η равен:

       Из (5.4.7) видно, что η < 1, зависит от разности температур между нагревателем и холодильником (и не зависит от конструкции машины и рода рабочего тела). Это ещё одна формулировка теоремы Карно. Цикл Карно, рассмотренный нами, был на всех стади ях проведен так, что не было необратимых процессов (не было соприкосновения тел с разными температурами). Поэтому здесь самый большой КПД. Больше получить в принципе невозможно.Любой процесс, не удовлетворяющий условию обратимости, мы называем необратимым процессом. Примером необратимого процесса является процесс торможения тела под действием сил трения. При этом скорость тела уменьшается, и оно останавливается. Энергия механического движения тела расходуется на увеличение энергии хаотического движения частиц тела и окружающей среды. Происходитдиссипация энергии. Для продолжения движения необходим компенсирующий процесс охлаждения тела и среды. В нашем случае тепловых машин, нагреватель и холодильник – не идеальны, они не обладают бесконечной теплоёмкостью и в процессе работы получают или отдают добавочную температуру ΔТ.

Рис. 5.6

Как видно из рисунка, площадь внутри фигуры ABCD уменьшилась из-за потерь, значит уменьшилась полезная работа цикла и КПД.

Для обратимого цикла Карно      

 Для необратимого цикла

Таким образом, КПД всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше КПД цикла Карно. Т.е. всегда  – этот вывод справедлив независимо от причин необратимости циклического процесса.

      Холодильная машина

Холодильная машина – это машина, работающая по обратному циклу Карно (рис. 5.4). То есть если проводить цикл в обратном направлении, тепло будет забираться у холодильника и передаваться нагревателю (за счет работы внешних сил).

Обратный цикл Карно можно рассмотреть на примере рис. 5.5. При изотермическом сжатии В–А, от газа отводится количество теплоты Q₁при Т₁. В процессе изотермического расширения D–С к газу подводится количество теплоты Q₂.

В этом цикле  ,   и работа, совершаемая над газом, отрицательна, т.е.

       Если рабочее тело совершает обратный цикл, то при этом можно переносить энергию в форме тепла от холодного тела к горячему за счет совершения внешними силами работы.

       Для холодильных машин, работающих по циклу Карно

 для процесса, происходящего по замкнутому циклу

(6.1.2)

       Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение   есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Это позволяет ввести новую функцию состояния S:

Функция состояния, полный дифференциал которой равен  , называется энтропией (от греч. entropia – поворот, превращение) – мера способности теплоты превращаться в другие виды энергии. 

Энтропия S – это отношение полученной или отданной теплоты к температуре, при которой происходил этот процесс. 

Для обратимых процессов изменение энтропии, как следует из (6.1.2),

       Это выражение называется равенство Клаузиуса.

 Энтропия системы является функцией ее состояния, определенная с точностью до произвольной постоянной.  Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

       Таким образом, по формуле (6.2.1) можно определить энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно. Физический смысл имеет лишь разность энтропий.         Исходя из этого, найдем изменения энтропии в процессах идеального газа.         Так как при Т = const, , или 

Таким образом, изменение энтропии ΔS_1-2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида перехода 1 - 2.         Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:

изохорический:   , т.к.  ; изобарический:   т.к. Р₁ = Р₂; изотермический:   т.к.  ;

адиабатический:   , т.к. 

       Отметим, что в последнем случае адиабатический процесс называют изоэнтропийным процессом, т.к.  .

 Итак, энтропия – отношение полученной или отданной системой теплоты в обратимом процессе к температуре, при которой происходит эта передача.

.

 Энтропия – величина аддитивная, т.е. она равна сумме энтропий всех тел, входящих в систему: .   Обратимый цикл Карно  Из п. 5.2 мы знаем, что в тепловой машине, работающей по принципу Карно, имеются три тела: холодильник, нагреватель, рабочее тело (газ).

       Изменение энтропии газа в тепловой машине   так как газ возвращается в исходное состояние. Изменение энтропии нагревателя:

       Для холодильника:

    или т.е. S – константа. Таким образом, мы пришли к выражению, полученному в п. 6.1, называемому равенство Клаузиуса.

Необратимый цикл Карно

       Мы знаем, что   т.е.        Отсюда   тогда         Таким образом,   или  Это выражение называют неравенством Клаузиуса: при любом необратимом процессе в замкнутой системе энтропия возрастает (dS > 0). Значит для замкнутой системы Это выражение – математическая запись второго начала термодинамики. Выражения (6.5.1) и (6.5.2) можно объединить:

 Закон возрастания энтропии:   Энтропия замкнутой системы при любых происходивших в ней процессах не может убывать (или увеличивается, или остается неизменной). Посмотрим на энтропию с другой стороны. Макросостояние – это состояние вещества, характеризуемое его термодинамическими параметрами. Состояние же системы, характеризуемое состоянием каждой входящей в систему молекулы, называют микросостоянием. Так как молекулы движутся хаотически, то имеется много микросостояний, соответствующих одному макросостоянию. Обозначим W - число микросостояний, соответствующее данному макросостоянию (как правило, W >> 1). Термодинамической вероятностью или статистическим весом макросостояния W - называется число микросостояний, осуществляющих данное макросостояние (или число перестановок одноименных элементов, при которых сохраняется данное макросостояние). Термодинамическая вероятность W - максимальна, когда система находится в равновесном состоянии. В состоянии равновесия и термодинамическая вероятность максимальна, и энтропия максимальна. Из этого можно сделать вывод, что между ними существует связь. Энтропия S – аддитивная величина:  , где   - сумма энтропий тел, входящих в систему. Вероятность сложного события, есть произведение вероятностей состояний: где W₁ – первое состояние; W₂ – второе состояние.

       Аддитивной величиной является логарифм термодинамической вероятности:          Поэтому Л. Больцман предложил: где k – коэффициент Больцмана. С этой точки зрения энтропия выступает, как мера беспорядочности, хаотичности состояния.   Например, в ящике черные и белые шары. Они порознь, есть порядок и W невелика. После встряхивания – шары перемещаются, Wувеличивается и энтропия тоже. И сколько бы не встряхивать потом ящик, никогда черные шары не соберутся у одной стенки, а белые у другой, хотя эта вероятность не равна нулю. Связь между S и W позволяет несколько иначе сформулировать второе начало термодинамики: наиболее вероятным изменением энтропии является ее возрастание. Энтропия – вероятностная статистическая величина. Утверждение о возрастании энтропии потеряло свою категоричность. Её увеличение вероятно, но не исключаются флуктуации. Энтропия замкнутой системы – максимальна, при достижении системой равновесного состояния.

Второй закон термодинамики: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара. ИЛИ Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой.

   Первое и второе начала термодинамики не позволяет определить значение энтропии при абсолютном нуле Т = 0 К.

С точки зрения физики, второе начало термодинамики применимо для замкнутых систем (система считается замкнутой, если у неё отсутствует энергетический обмен с внешним миром). Открытые (т.н. "диссипативные") системы, изучением которых занимается неравновесная термодинамика, основателем которой был русский учёный И. Пригожин, второму началу термодинамики не подчиняются. Действительно, можно представить себе ситуацию, когда в систему можно внести упорядочение извне, либо система имеет предпосылки к самоорганизации. В этом случае энтропия будет уменьшаться.

Термодинами́ческие потенциа́лы (термодинамические функции) — характеристические функции в термодинамике, убыль которых в равновесных процессах, протекающих при постоянстве значений соответствующих независимых параметров, равна полезной внешней работе.

Термин был введён Пьером Дюгемом, Гиббс в своих работах использовал термин «фундаментальные функции». Выделяют следующие термодинамические потенциалы:

• внутренняя энергия

• энтальпия

• свободная энергия Гельмгольца

• потенциал Гиббса

• большой термодинамический потенциал

№21

Реальные газы и жидкости. Силы взаимодействия между атомами и молекулами. Уравнение состояния реальных газов Ван-дер-Ваальса. Молекулярные силы в жидкостях. Поверхностно натяжение. Капиллярные явления.

Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации. Так, для газов с низкой температурой сжижения (He, H₂, Ne и даже N₂, O₂, Ar, CO, CH₄) при давлениях до 50 атм. отклонения не превышают 5 %, а при давлениях до 10 атм. – 2 %. Легко конденсирующиеся газы (CO2, SO₂, Cl₂, CH₃Cl) уже при 1 атм. обнаруживают отклонения до 3 %.

Реальные газы – газы, свойства которых зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия межмолекулярного взаимодействия много меньше средней кинетической энергии молекул, свойства реальных и идеальных газов отличаются незначительно. Поведение этих газов резко различно при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.

   Ван–дер–Ваальс, объясняя свойства реальных газов и жидкостей, предположил, что на малых расстояниях между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. Межмолекулярные взаимодействия имеют электрическую природу и складываются из сил притяжения (ориентационных, индукционных) и сил отталкивания.

Ориентационные силы действуют между полярными молекулами – молекулами, обладающими дипольными или квадрупольными моментами. Сила притяжения между молекулами зависит от их взаимной ориентации, поэтому они и называются ориентационными. Хаотическое тепловое движение непрерывно меняет ориентацию полярных молекул, но среднее по всем ориентациям значение силы не равно нулю (рис. 7.1).

  Рис. 7.1

       Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия равно U_ор(r) ~ p₁ p₂ r^-6, где p₁,p₂ – дипольные моменты взаимодействующих молекул. Сила ориентационного взаимодействия F_ор = – dU/dr ~ r^-7 убывает с расстоянием значительно быстрее, чем кулоновская сила взаимодействия заряженных частиц F_кул ~ r^{– 2}.

  Индукционные (поляризационные) силы действуют между полярной и неполярной молекулами, а также между полярными молекулами. Полярная молекула создает электрическое поле, которое поляризует другую молекулу – индуцирует в ней дипольный момент. Потенциальная энергия межмолекулярного взаимодействия в этом случае пропорциональна дипольному моменту p₁ полярной молекулы и поляризуемости α₂второй молекулы: U_инд ~ p₁α₂ r– 6. Индукционные силы убывают по тому же закону, что и ориентационные F_инд ~ r^–7.

  Дисперсионное молекулярное взаимодействие возникает благодаря виртуальному нарушению электронейтральности молекулы в отдельные моменты времени. Мгновенный диполь поляризует соседние молекулы – возникает взаимодействие мгновенных диполей. Данное взаимодействие называется дисперсионным, его энергия определяется поляризуемостью молекул α₁, α₂: U(r) ~ α₁α₂ r^–6, а сила убывает по законуF_дисп ~ r^–7. Обычно дисперсионные силы превосходят ориентационные и индукционные. Например, при взаимодействии таких полярных молекул, как СО, НI, HBr и др., F_дисп в десятки и сотни раз превосходят все остальные.

Отметим, что все три силы и энергии одинаковым образом убывают с расстоянием:        F = F_ор + F_инд + F_дисп ~ r^–7,   U = U_ор + U_инд + U_дисп ~ r^–6.

        Силы отталкивания действуют между молекулами на очень малых расстояниях, когда происходит взаимодействие электронных оболочек атомов, входящих в состав молекул. Принцип Паули запрещает проникновение заполненных электронных оболочек друг в друга. Возникающие при этом силы отталкивания зависят в большей степени, чем силы притяжения от индивидуальных особенностей молекул. К хорошему согласию с данными экспериментов приводит допущение, что потенциальная энергия сил отталкивания возрастает с уменьшением расстояния по закону U_от(r) ~ r^–12, а, соответственно, сила отталкивания растет как F_от ~ r^–13. Полагаем, что U(r = ¥) = 0 – при больших расстояниях потенциальная энергия взаимодействия равна нулю. В этом случае кривая взаимодействия описывается потенциалом Леннарда – Джонса (рис. 7.2)       U( r) = – ar^–6 + br^–12.     Глубина потенциала равна U(r_min) = –a²/4b при r_min = (2b/a)^1/6 – расстоянии, соответствующем наибольшей энергии связи молекул. Отметим, что в данном потенциале не учтены ориентационные взаимодействия, существенные для многоатомных молекул и кристаллов.

Уравнение Ван–дер–Ваальса (7.1.2) – одно из первых уравнений состояния реального газа. Данное уравнение учитывает конечные размеры всех молекул, что становится существенным при больших давлениях, а также притяжение молекул в результате межмолекулярного взаимодействия.

Уравнение состояния реального газа, предложенное Ван–дер–Ваальсом можно получить из следующих рассуждений. Учтем влияние конечных размеров молекул на уравнение состояния реального газа. Давление определяется средней кинетической энергией теплового движения всех молекул Р = nkT. 7.2.1        При конечных размерах молекул, имеющих радиус r, область 4p(2r)³/3 вокруг каждой из молекул будет недоступна для попадания в нее другой неточечной молекулы. В результате в сосуде, содержащем N молекул конечных размеров, область объемом (N/2)4p(2r)³/3 = 4NV_молек (V_молек = 4pr³/3 – объем одной молекулы) будет недоступна для столкновений. Поэтому можно считать, что половина всех молекул занимает объем b = 4NV_молек и покоится, а другая половина представляет собой точечные молекулы и движется с удвоенной кинетической энергией, обладая температурой Т´ = 2Т. Объем, доступный точечным молекулам, будет равен V - b, а давление, оказываемое на стенки сосуда, определяется точечными подвижными молекулами (N´ = N/2):        Р = n´kT´ =  Если в сосуде находится один моль газа, то уравнение состояния примет вид (N = N_A, N_Ak = R, b = 4N_AV_молек):        P(V - b) = RT.

Д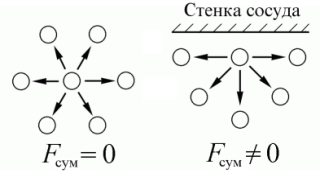 ля v = m/m молей газа уравнение состояния газа с учетом конечного размера молекул примет видP(V - nb) = nRT. Отметим, что это уравнение является приближенным и выведено в предположении только парных столкновений. При больших давлениях это условие уже не выполняется, и возможно одновременное соприкосновение трех и более частиц, а такие случаи были исключены из рассмотрения. Рассмотрим теперь влияние сил притяжения на уравнение состояния идеального газа. Будем считать для простоты частицы газа точечными. Наличие сил притяжения между ними, действующих на больших расстояниях, приводит к появлению дополнительного внутреннего воздействия на газ. Это обусловлено тем, что в то время как в объеме газа действие сил притяжения между молекулами в среднем уравновешивается, на границе «газ – стенка сосуда» действие сил притяжения со стороны газа остается не скомпенсированным, и появляется избыточная сила, направленная в сторону газа (рис. 7.3). В результате избыточное внутреннее давление P_i (i - intrinsic) будет пропорционально квадрату концентрации числа частиц P_i ~ n_S n_V ~ N ²/V ²,        где N – полное число частиц в сосуде объема V. Если N = N_A – в сосуде находится один моль газа, то запишем        P_i = a/V ²,  где а – постоянная величина, своя для каждого сорта газа. В случае v-молей имеем        P_i = v²a/V ²С учетом внутреннего давления уравнение состояния примет вид P + P_i = nkT. Давление P_i не зависит от материала стенки, в противном случае удалось бы создать вечный двигатель первого рода. Роль стенки может играть и сам газ. Достаточно для этого выполнить мысленное сечение произвольной плоскостью любой внутренней области объема газа. Полученное уравнение, с учетом выражения для P_i переходит в новое уравнение состояния реального газа при наличии сил притяжения: (P + v² a/V ²)V = vRT. Учитывая совместное действие сил притяжения и сил отталкивания и полученные поправки для объема и давления в уравнении Менделеева – Клапейрона, получим уравнение Ван–дер–Ваальса для реального газа: (P + v² a/V ²)(V - vb) = vRT, (7.2.3) или для одного моля: Данное уравнение справедливо при условии vb << V и v²a/V ² << P. Помимо этого предполагается, что частицы газа сферически симметричны. Поскольку реально это не так, то даже для неплотных газов величины а и b зависят от температуры. 

Молекулярные силы в жидкостях:

а)  Силы сцепления.

 Капля жидкости, освобожденная от действия внешних сил, принимает форму шара. При ш аровой форме силы сцепления, действующие между молекулами, оказываются полностью симметричными.

б) Краевые эффекты.

  На границу жидкости у стенки сосуда действуют одновременно силы сцепления между молекулами жидкости К и силы взаимодействия жидкости и материала стенок А. В зависимости от того, какие из них больше, жидкость называется смачивающей и несмачивающей (рис. 97 и 98).

в) Диффузия и осмос.

  Диффузией называется смешивание двух соприкасающихся жидкостей или газов различной плотности, происходящее независимо от действия силы тяжести (иногда вопреки ему), благодаря подвижности молекул. При этом общий объем смешавшихся веществ иногда становится меньше суммы объемов смешивающихся веществ (например, при диффузии спирта в воду).

  Осмосом называется смешение двух жидкостей или газов через пористую перегородку, пропускающую молекулы одного из веществ, но задерживающих молекулы другого вещества. При этом давления по обе стороны перегородки изменяются. Осмотическое давление играет существенную роль при поднятии питательных соков по стеблям растений, а также в процессах, происходящих в клетках организмов.

Свойства жидкостей:

1. Плохо сжимаема

2. Текучесть (занимает форму сосуда)

3. Поверхностная энергия

Молекулы на поверхности обладают большей энергией, чем молекулы внутри жидкости. Это связано с тем, что чтобы молекулы перешли из глубины на поверхность необходимо совершить работу.

Поверхностный слой жидкости находится в упругом состоянии.

Сила поверхностного натяжения стремиться уменьшить свободную поверхность жидкости. Она действует на любую линию поверхностного слоя, перпендикулярно ей и по касательной к поверхности.

Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:

• в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма).

• струя воды «слипается» в цилиндр.

• маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так каксила тяготения меньше силы, препятствующей увеличению площади жидкости.

• некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.

• На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.

Площадь поверхности

С поверхностью жидкости связана свободная энергия

где   — коэффициент поверхностного натяжения,   — полная площадь поверхности жидкости^[4]. Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля принимает форму шара, однако при более сложных условиях задача о форме поверхности жидкости становится исключительно сложной.

Формула Лапласа

Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется существование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и даётся формулой Лапласа:

Здесь   — радиусы главных кривизн в точке. Они имеют одинаковый знак, если соответствующие центры кривизны лежат по одну сторону от касательной плоскостив точке, и разный знак — если по разную сторону. Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому

Для случая поверхности кругового цилиндра радиуса   имеем Обратите внимание, что   должно быть непрерывной функцией на поверхности плёнки, так что выбор «положительной» стороны плёнки в одной точке локально однозначно задаёт положительную сторону поверхности в достаточно близких её точках.

Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.

С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре.

Методы определения поверхностного натяжения:

Смачиваемость и капиллярные явления

Смачиваемость — предпочтительное распространение флюида по поверхности твердого тела и его прилипание к этой поверхности в присутствии других не смешивающихся флюидов.Смачиваемость влияет на: распределение флюидов в системе пор, так как смачиваемость определяет распределение флюидов в пласте; движение флюидов, так как от смачиваемости породы зависит относительная проницаемость. Количественной характеристикой смачиваемости является краевой угол смачиваемости — θ_с.

В основном все пласты являются гидрофильными, т.е. предпочтительно смачиваемые водой.

М ежфазное натяжение — сила, действующая на единицу длины двух несмешивающихся фаз. Таким образом, межфазное натяжение является мерой смешиваемости. При высоком значении межфазного натяжения жидкости не смешиваются, при низком значении — жидкости более подвержены смешиванию. На рисунке ниже представлена система вода — нефть —порода.

Угол θ, образованный касательной к капле в точках ее периметра, зависит от поверхностных натяжений σ₁₂, σ₂₃, и σ₁₃ на разделах фаз 1-3, 1-2 и 2-3. Угол всегда отсчитывают от касательной в сторону воды.

Из условия равновесия векторов (предполагая, что краевой угол 0 отвечает термодинамическому равновесию) получим: где σ₁₂ — поверхностное натяжение на границе вода-нефть, Н/м; σ₁₃ — поверхностное натяжение на границе вода-порода, Н/м; σ₂₃ — поверхностное натяжение на границе нефть-порода, Н/м; θ — угол смачивания, град;

Капиллярное давление — это перепад давлений на границе раздела двух несмешивающихся жидкостей, одна из которых смачивает поверхность породы лучше другой. На рисунке ниже показана граница радела фаз в системе вода — нефть.

У равнения капиллярного давления для такой системы записывается в виде: где р_к — капиллярное давление, Па; σ_нв — поверхностное натяжение на границе нефть-вода, Н/м; θ — угол смачивания, град; r — радиус капилляра (пор), м. Из уравнения следует, что капиллярное давление:

• прямо пропорционально межфазному натяжению;

• обратно пропорционально радиусу капилляра (т.е. силы капиллярного давления выше в капиллярах (порах) меньшего радиуса);

• заставляет смачивающие жидкости пропитывать более мелкие поры, а не смачивающие — более крупные.

22 вопрос.

Фазовые переходы и фазовые диаграммы. Кристаллическое состояние и его параметры. Скрытые теплоты фазовых превращений. Уравнение Клайперона-Клаузиса. Кристаллическое и аморфное состояние вещества. Способы определения и описания кристаллических структур.

1)Фа́зовыйперехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.

Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.

Наиболее часто рассматриваются фазовые переходы при изменении температуры, но при постоянном давлении (как правило равном 1 атмосфере). Именно поэтому часто употребляют термины «точка» (а не линия) фазового перехода, температура плавления и т. д. Разумеется, фазовый переход может происходить и при изменении давления, и припостоянных температуре и давлении, но и при изменении концентрации компонентов (например, появление кристалликов соли в растворе, который достиг насыщения).

Классификация фазовых переходов

При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём, количество запасённой внутренней энергии, концентрация компонентов и т. п. Подчеркнём: имеется в виду скачкообразное изменение этих величин при изменении температуры, давления и т. п., а не скачкообразное изменение во времени (насчёт последнего см. ниже разделДинамика фазовых переходов).

Наиболее распространённые примеры фазовых переходов первого рода:

• плавление и кристаллизация

• испарение и конденсация

• сублимация и десублимация

При фазовом переходе второго рода плотность и внутренняя энергия не меняются, так что невооружённым глазом такой фазовый переход может быть незаметен. Скачок же испытывают их производные по температуре и давлению: теплоёмкость, коэффициент теплового расширения, различные восприимчивости и т. д.

Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться). Описание фазового перехода второго рода как следствие изменения симметрии даётся теорией Ландау. В настоящее время принято говорить не об изменении симметрии, но о появлении в точке перехода параметра порядка, равного нулю в менее упорядоченной фазе и изменяющегося от нуля (в точке перехода) до ненулевых значений в более упорядоченной фазе.

Наиболее распространённые примеры фазовых переходов второго рода:

• прохождение системы через критическую точку

• переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность)

• переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата)

• переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты)

• переход аморфных материалов в стеклообразное состояние

Современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода.

В последнее время широкое распространение получило понятие квантовый фазовый переход, т.е. фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур, где классический фазовый переход не может реализоваться вследствие теоремы Нернста.

фазовая диаграмма иначе диаграмма состояния (англ. phasediagram) —графическое изображение состояний термодинамической системы в пространстве основных параметров состояния — температуры T, давления p и состава x.

2)Критическое состояние (критич. фаза), состояние двухфазной системы, в котором сосуществующие в равновесии фазы (напр., жидкость и ее насыщ. пар или две несмешивающиеся жидкости) становятся тождественными по всем своим свойствам. Параметры критического состояния системы (давление р_к, т-раТ_к, объем V_к, состав x_к и др.) наз. критич. параметрами. За пределами критическое состояние сосуществование рассматриваемых фаз в равновесии невозможно, система превращ. в однофазную (гомогенную). В этом смысле критическое состояние является предельным случаем двухфазного равновесия.

В критическом состояния поверхностное (межфазное) натяжение на границе раздела сосуществующих фаз равно нулю, поэтому вблизи критическое состояние легко образуются системы, состоящие из мн. капель или пузырьков (эмульсии, аэрозоли, пены). Вблизи критического состояния резко возрастает величина флуктуации плотности (в случае чистых веществ) и концентраций компонентов (в многокомпонентных системах), что приводит к значит.изменению ряда физ. свойств вещества (см. Критические явления).

При приближении к критическму состоянию свойства сосуществующих в равновесии фаз (плотность, теплоемкость и др.) изменяются постепенно, без скачка. Поэтому критическое состояние наблюдается лишь при равновесии изотропных фаз [жидких и (или) газовых] или кристаллич. фаз с одинаковым типом решетки. Независимо от природы сосуществующих фаз (типа двухфазного равновесия) и числа компонентов в критическое состояние система имеет вариантность на 2 меньше, чем в обычном гомогенном состоянии

3)СКРЫТАЯ ТЕПЛОТА, теплота, поглощаемая или выделяемая веществом при ФАЗОВОМ превращении (вещества) при постоянной температуре - из твердого состояния в жидкое или из жидкого в газообразное. Когда тает лед, его температура остается неизменной до тех пор, пока он полностью не превратится в воду. Теплота, необходимая для этого, называется скрытой теплотой плавления.Точно так же, теплота, необходимая для преобразования воды в пар при постоянной температуре, называется скрытой теплотой испарения.

4) Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением

где   — удельная теплота фазового перехода,   — изменение удельного объёма тела при фазовом переходе.

5)Кристаллическое Вещество - КРИСТАЛЛИЧЕСКОЕ ВЕЩЕСТВО, твердое вещество, у которого атомы или молекулы образуют правильную упорядоченную решетку. Большинство твердых веществ существует в кристаллическом состоянии, которое отличается повышенной стабильностью, но это не означает, что они имеют кристаллы в прямом смысле этого слова; например, чистая медь является кристаллической только потому, что ее атомы расположены в регулярном порядке.

АМОРФНОЕ ВЕЩЕСТВО, твердое вещество, не имеющее кристаллической структуры. Его атомы и молекулы расположены без соблюдения регулярности. Переохлажденные жидкости, такие как стекло, резина и некоторые пластмассы, являются аморфными. Многие порошки кажутся аморфными, но они обладают микрокристаллической структурой.