7) Закон сохранения и превращения энергии в механике. Космические скорости искусственных спутников и космических кораблей. Условия равновесия механических систем.

Зако́нсохране́нияэне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципомсохранения энергии.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: A = –(E_р2 – E_р1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

Следовательно  или E_k1 + E_p1 = E_k2 + E_p2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = E_k + E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

Космическая скорость (первая v₁, вторая v₂, третья v₃ и четвёртая v₄) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:

v ₁ (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности); v₂ (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность;; v₃ — покинуть звёздную систему, преодолев притяжение звезды;; v₄ — покинуть галактику.

В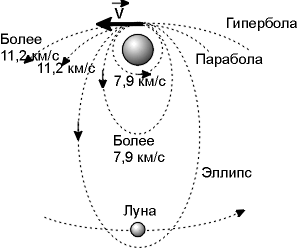 торая космическая скорость в   раза больше первой.

Первая космическая скорость - формула:

Первой космической скорости недостаточно для того чтобы тело могло выйти из сферы земного притяжения.

Условие равновесия механических систем

Механическая система будет находиться в равновесии, если на неё не будет действовать сила. Это условие необходимое, но не достаточное, так как система может при этом находиться в равномерном и прямолинейном движении.  Рассмотрим пример, изображенный на рис. 1   Здесь, даже при отсутствии силы, положение в точке  x2  нельзя назвать устойчивым равновесием. По определению,  Fx = 0  – условие равновесия системы.         Учитывая формулы F=-((dU/dx)i+(du/dy)j+(dU/dt)k) F=-gradU имеем   .         Следовательно, система будет находиться в состоянии равновесия, если Именно так находят положение точек экстремума.         Возвращаясь к рисунку 5.7, заметим, что    при  x = x1  и  x = x2.        Точка  x = x1  соответствует состоянию устойчивого равновесия (потенциальный барьер), тогда как точка  x = x2  - состоянию неустойчивого равновесия (потенциальная яма).      Таким образом, достаточным условием равновесия является равенство минимуму значения U (это справедливо не только для механической системы, но, например, и для атома).