Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением  , где   — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),   — большая полуось. Величина   называется эксцентриситетом эллипса. При  , и, следовательно,   эллипс превращается в окружность.

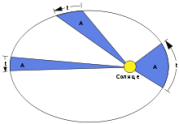
Второй закон Кеплера (закон площадей)

К аждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где   и   — периоды обращения двух планет вокруг Солнца, а   и   — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:  , где   — масса Солнца, а   и   — массы планет.

5. Системы материальных точек. Центр масс и теорема о его движении. Момент силы и момент количества. Законы сохранения импульса и момента импульса.

Материа́льнаято́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Совокупность мат. точек образует систему.

Состояние системы из N точек с известными массами определяется заданием координат и скоростей всех точек системы. На каждую материальную точку системы действуют силы как со стороны других точек, так и сто стороны сторонних внешних тел.

У равнение движения i-ой точки ситемы с массой mi:

(11.1) где fik-внутренняя сила действующая на i-ю точку со стороны к-й, а результующая внешняя сила Fi.

 Центр масс и теорема о его движении.

Для всякой системы мат точек существует точка пространства, называемая центром масс, или центром инерции. По определению, центр масс С расположен относительно точек системы так, что сумма произвдений масс mi точек на их радиус-векторы liотносительно центра масс равна нулю:

П олучим формулу выражающую радиус-вектор rс в любой СО чрез их массы и радиус векторы. Как видно из рисунка 22:

Li=ri-rc, и формула 12 принимает следующий вид: откуда

И получаем формулу для радиус-вектора центра масс: .

Из этого следует, что для системы состоящей из двух мат точек, m1l1+m2l2=0, откуда m1l1=-m2l2, и l1/l2=m2/m1, т.е. центр масс лежит на прямой соединяющей точки, на расстояниях обратно пропорциональных массе. . Из формулы 12 следует что положение ЦМ на изменится если две материальные точки системы заменить одной, обладающей их суммарной массой и расположить ее в центре масс этих точек.

Свойство центра масс – его уравнение движения имеет вид второго закона Ньютона. Для доказательства получим сначала формулы для скорости и ускорения центрамасс, дифференцирую по времени выражение 12:

Из 12.4 находим , где - полная масса системы. Сумму стоящую в правой части равенства выразим через силы, записав уравнения второго закона Ньютона по форме 11.1 для каждой точки системы и суммируя их:

Сумма унетренних сил равна нулю , так как из второго закона Ньютона: , и при суммирувании внутренние силы попарно уничтожаются, и таким образом: .

Это уравнение имеющее вид второго закона Ньютона, назвается законно (теоремой) о движении ЦМ: ЦМ системы мат точек движется как мат точка , в которой сосредоточена вся масса системы и к которой приложены все внешние силы действующие на систему.

Момент силы и момент количества.

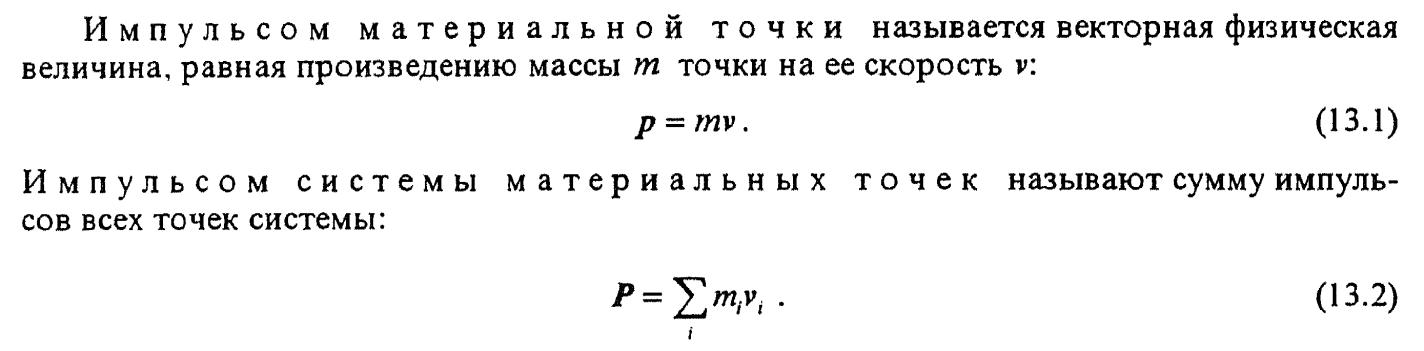
Закон Сохранения Импульса

Импульсом называют векторную величину, равную произведению массы тела на ее скорость:

При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:

Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса.

Рассмотрим неупругое столкновение, при котором выполняется закон сохранения импульса. Пусть при абсолютно неупругом столкновении двух тел их скорость будет общей после удара. Ее нужно определить. Напишем векторное уравнение, соответствующее закону сохранения импульса системы:

После проецирования векторов на выбранную ось получим скалярное уравнение, которое позволит определить искомую величину v_общ. Еще один пример - реактивное движение. Рассмотрим простейший случай этого движения, при котором происходит одномоментное взаимодействие - выстрел из винтовки.

Д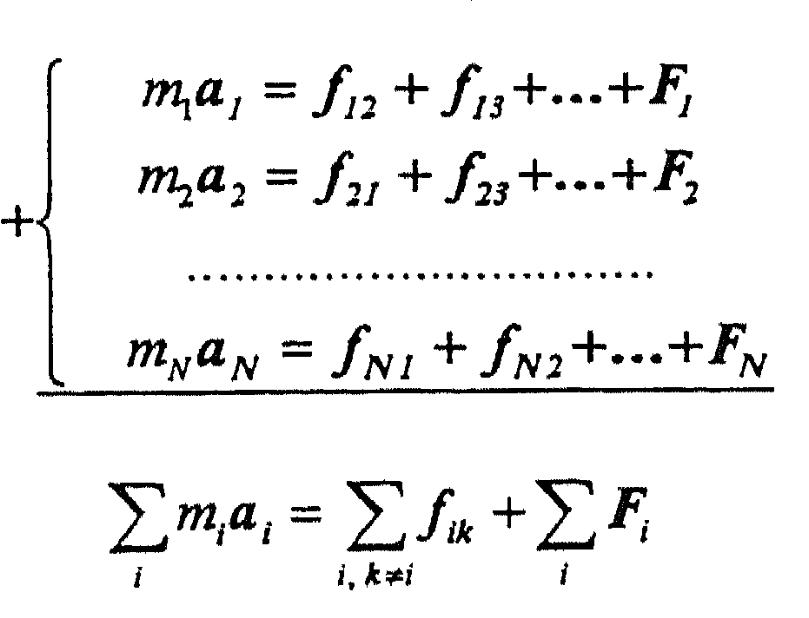 о выстрела скорости винтовки и пули были равны нулю. После выстрела они имели различные скорости. Если известна скорость пули, ее масса и масса ружья, можно определить скорость, которую приобрело ружье после выстрела:

Отсюда после проецирования векторов на выбранную ось получим:

	Закон сохранения момента импульса

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.         Поэтому  , то есть или                 Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.         Это один из фундаментальных законов природы.         Аналогично для замкнутой системы тел, вращающихся вокруг оси z:          отсюда                   или          .        Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.         Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.  Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского