11.Символический метод расчета и его применение при негармонических периодических воздействиях.

В основе расчета линейных электрических цепей, находящихся под воздействием периодических несинусоидальных сигналов, лежит принцип наложения. Его суть заключается в разложении несинусоидального периодического сигнала в одну из форм ряда Фурье.

Таким образом, расчет цепей при периодическом несинусоидальном воздействии включает в себя:

1) задачу анализа спектрального состава сигнала (разложение его в ряд Фурье);

2) расчет цепи по каждой гармонической составляющей;

3) задачу синтеза, в результате которого определяется результирующий выходной сигнал как функция времени или частоты или его действующие или амплитудные значения.

При решении задачи анализа обычно используется тригонометрическая или комплексная форма ряда Фурье с ограниченным числом членов разложения, что приводит к некоторой погрешности аппроксимации истинного сигнала.

Расчет цепи по каждой гармонической составляющей осуществляется обычно символическим методом. При этом необходимо иметь в виду, что на -й гармонике индуктивное сопротивление , а емкостное сопротивление , т.е. на -й гармонике индуктивное сопротивление в раз больше, а емкостное в раз меньше, чем на первой гармонике.

После определения искомых токов и напряжений от отдельных гармоник методом наложения находится результирующая реакция цепи на несинусоидальное периодическое воздействие. При этом определяется либо мгновенное значение результирующего сигнала на основании расчета амплитуд и фаз отдельных гармоник, либо его амплитудные или действующие значения. При определении результирующей реакции недопустимо геометрически (векторное представление) складывать комплексные амплитуды отдельных гармоник, так как вектора различных гармоник вращаются с различной угловой скоростью.

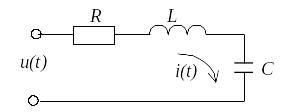
12. Последовательная rlc-цепь в цепи синусоидального тока, её частотные характеристики.

Явление резонанса возможно в цепях содержащих не менее двух энергоёмких элементов. Среди таких цепей различают последовательные цепи и параллельные цепи.

; ; . Тогда .

Последнее уравнение может быть записано в комплексной форме:

или после подстановок ,

где - комплекс действующего значения напряжения, - комплекс действующего значения тока, - действующее значение напряжения.

Модуль - полное сопротивление цепи определяется по формуле , а фазовый сдвиг . Их частотные зависимости приведены ниже:

Из анализа этих характеристик можно сделать следующие выводы:

1) при полное сопротивление , а ;

2) при полное сопротивление , а ;

3) при полное сопротивление ;

13.Активная, реактивная и полная мощность в цепи синусоидального тока. Баланс мощностей. Условия передачи максимальной мощности. Измерение мощности.

В выражении закона Ома для цепи синусоидального тока присутствует множитель , называемый комплексным сопротивлением цепи. , где - активное сопротивление, - реактивное сопротивление.

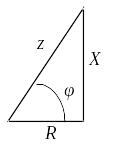
можно представить как гипотенузу прямоугольного треугольника, называемого треугольником сопротивлений, один катет которого равен , а другой - .

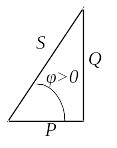
Если умножить каждую сторону треугольника сопротивлений на , или каждую сторону треугольника проводимостей на , то получится треугольник мощностей.

Под активной мощностью понимается среднее значение мгновенной мощности за период . ,где - коэффициент мощности.

Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи в сопротивлении . Единица активной мощности – Вт.

Под реактивной мощностью понимают произведение напряжения на участке цепи на ток по этому участку и на синус угла между напряжением и током : . Единица реактивной мощности – вольт-ампер реактивный (ВАр).

Реактивная мощность пропорциональна среднему за четверть периода значению энергии.

Гипотенуза треугольника мощностей называется полной мощностью. Она связана с активной и реактивной мощностями цепи следующей зависимостью: . Единица полной мощности – ВА. Комплексная мощность .

Условие передачи максимальной мощности в нагрузку выполняется при , то есть (мощность, вырабатываемая генератором, является чисто активной). Для выполнения этого условия необходимо, чтобы комплексное сопротивление нагрузки было комплексно сопряженным с комплексным сопротивлением генератора , где . Выполнение этого условия возможно только при .

Измерение мощности осуществляется обычно с помощью ваттметра электродинамической системы.

.

Это уравнение отражает баланс комплексной мощности, согласно которому сумма комплексных мощностей, потребляемых всеми ветвями цепи, равна нулю.