
- •Матрица, виды матриц, действия над матрицами.
- •Свойства операций над матрицами:
- •Определители второго и третьего порядка (основные понятия, св-ва, вычисления)
- •Минор. Алгебраическое дополнение. Теорема Лапласа.
- •Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов.
- •5.Приведение матрицы к ступенчатому виду. Элементарные преобразования строк и столбцов.
- •Обратная матрица. Способы нахождения.
- •Вычисление определителей высших порядков. Теорема Лапласа. Приведение определителя к ступенчатому виду.
- •Классификация систем линейных уравнений. Решение системы 3-х линейных уравнений с тремя неизвестными. Метод Гаусса, метод Крамера, матричный метод.
- •Система n- линейных уравнений с m переменными. Теорема Кроникера-Капелли. Базисное и частное решения.
- •11.Векторы, основные понятия, действия над векторами в геометрической и координатной форме.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Проекция вектора на ось
- •Свойства проекций
- •Расстояние между двумя точками. Деление отрезка в данном отношении
- •Скалярное произведение векторов. Определение скалярного произведения векторов. Свойства скалярного произведения. Понятие скалярного произведения
- •Угол между векторами и значение скалярного произведения
- •Скалярный квадрат вектора Свойства скалярного произведения
- •13.Векторное произведение векторов. Его св-ва. Определение векторного произведения через координаты векторов. Нахождение площадей параллелограмма и треугольника.
- •14.Смешанное произведение векторов, его св-ва. Определение смешанного произведения через координаты векторов. Определение объема параллелепипеда и прямокгольной пирамиды.
- •Геометрические свойства смешанного произведения
- •Алгебраические свойства смешанного произведения
- •Формула вычисления смешанного произведения
- •15.Линейная зависимость и независимость системы векторов. Условия и свойства линейной зависимости векторов.
- •Свойства линейно зависимых и линейно независимых векторов
- •16.Базис векторного пространства и разложение вектора по базису.
- •17.Собственный вектор и собственное значение матрицы
- •18. Линейная модель обмена. Структура матриц.
- •19. Определение квадратичной формы
- •20. Критерий Сильвестра знакоопределенности квадратичной формы. (посмотреть в тетради)
- •21. Модель Леонтьева.
- •22. Элементы аналитической геометрии на плоскости. Уравнение прямой в зависимости от параметра. Длина отрезка и деление отрезка в заданном соотношении.
- •23. Условия параллельности и перпендикулярности прямых и угол между ними. Расстояние от точки до прямой.
- •24. Кривые 2-го порядка. Парабола. Эллипс. Гипербола.
- •25. Гипербола как дробно-рациональная функция.
- •26. Уравнение плоскости и прямой в пространстве. Плоскость и прямая в пространстве
- •28. Системы линейных неравенств с двумя неизвестными
Свойства проекций
При умножении вектора на число l его проекция на ось умножается на то же число:
![]() .
(2.3)
.
(2.3)
Проекция суммы векторов на одну и ту же ось равна сумме проекций составляющих векторов на ту же ось:
![]() .
(2.4)
.
(2.4)
Разложение вектора по осям координат:
Если ![]()
![]() -
векторы, по модулю равные единице и
направленные по координатным
осям Ox, Oy и Oz,
то разложение вектора
-
векторы, по модулю равные единице и
направленные по координатным
осям Ox, Oy и Oz,
то разложение вектора ![]() по
трем координатным осям выражается
формулой
по
трем координатным осям выражается
формулой
![]()
![]()
![]() (10)
(10)
где ax, ay и az -
проекции вектора a на
координатные оси - называются координатами
вектора (если вектор ![]() имеет
координаты ax, ay, az,
то это обозначается так:
{ax, ay, az}).
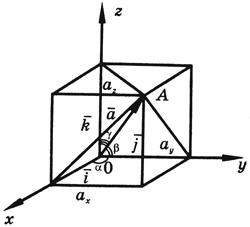
Если вектор
имеет
начало в начале координат, а его
конец A имеет
координаты x, y и z,
то тогда его проекции на координатные
оси равны координатам его конца:
имеет
координаты ax, ay, az,
то это обозначается так:
{ax, ay, az}).
Если вектор
имеет
начало в начале координат, а его
конец A имеет
координаты x, y и z,
то тогда его проекции на координатные
оси равны координатам его конца:
ax = x; ay = y; az = z.
В
этом случае вектор
называется
радиусом-вектором точки A.
Радиус-вектор точки обозначается
обыкновенно через ![]() (см.
рисунок):
(см.
рисунок):
![]()
![]()
![]() (11)
(11)
а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле
![]()
![]() (12)
(12)
Расстояние между двумя точками. Деление отрезка в данном отношении
Расстояние d между
двумя точками ![]() (
(![]() ,
, ![]() ,
, ![]() )
и
)
и ![]() (
(![]() ,
, ![]() ,
, ![]() )
в пространстве определяется формулой
)
в пространстве определяется формулой
![]() .
.
Координаты x,
y, z точки
М, которая делит отрезок ![]() ,
ограниченный точками
(
,
,
)
и
(
,
,
),
в отношении
,
ограниченный точками
(
,
,
)
и
(
,
,
),
в отношении ![]() ,
определяется по формулам
,
определяется по формулам
![]() ,
, ![]() ,
, ![]() .
.
В
частности, при ![]() имеет
координаты середины данного отрезка:
имеет
координаты середины данного отрезка:
![]() ,
, ![]() ,
, ![]() .
.
Скалярное произведение
Скалярное
произведение векторов ![]() и
и ![]() :
: ![]()
где ![]() -
угол между векторами
-
угол между векторами ![]() и
;
если
и
;
если ![]() либо
либо ![]() ,
то
,
то ![]()
Из
определения скалярного произведения
следует, что ![]() где,
например,
где,
например, ![]() есть
величина проекции вектора
на
направление вектора
.
есть
величина проекции вектора
на
направление вектора
.
Скалярный
квадрат вектора: ![]()
Свойства
скалярного произведения: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скалярное произведение в координатах
Если ![]()
![]() то
то ![]()
![]()
Угол между векторами
![]()
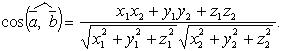
Векторное произведение
Векторное
произведение векторов
и
-
вектор, обозначаемый ![]()
![]() или
или ![]() для
когорого:
для
когорого:
1) ![]() (
-
угол между векторами
и
,
(
-
угол между векторами
и
, ![]() );
);
2) ![]()
3) тройка , , - правая.
Свойства
векторного произведения:![]()
![]()
![]()
![]()
![]()
![]() если
если ![]() ,
то
,
то ![]() равен
площади параллелограмма, построенного
на приведенных к общему началу
векторах
и
.
равен
площади параллелограмма, построенного
на приведенных к общему началу
векторах
и
.
Скалярное произведение векторов. Определение скалярного произведения векторов. Свойства скалярного произведения. Понятие скалярного произведения
Сначала про угол
между векторами.
Думаю, всем интуитивно понятно, что
такое угол между векторами, но на всякий
случай чуть подробнее. Рассмотрим
свободные ненулевые векторы ![]() и
и ![]() .
Если отложить данные векторы от
произвольной точки
.
Если отложить данные векторы от
произвольной точки ![]() ,
то получится картинка, которую многие
уже представили мысленно:
,
то получится картинка, которую многие
уже представили мысленно:
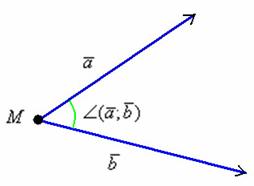
Признаюсь, здесь я обрисовал ситуацию только на уровне понимания. Если необходимо строгое определение угла между векторами, пожалуйста, обратитесь к учебнику, для практических же задач оно нам, в принципе, ни к чему. Также ЗДЕСЬ И ДАЛЕЕ я буду местами игнорировать нулевые векторы ввиду их малой практической значимости. Оговорку сделал специально для продвинутых посетителей сайта, которые могут меня упрекнуть в теоретической неполноте некоторых последующих утверждений.
Угол между векторами ![]() может
принимать значения от 0 до 180 градусов
(от 0 до
может
принимать значения от 0 до 180 градусов
(от 0 до ![]() радиан)
включительно. Аналитически данный факт
записывается в виде двойного
неравенства:
радиан)
включительно. Аналитически данный факт
записывается в виде двойного
неравенства: ![]() либо
либо ![]() (в
радианах).
(в
радианах).
В литературе значок
угла ![]() часто
пропускают и пишут просто
часто
пропускают и пишут просто ![]() .
.
Определение: Скалярным
произведением двух векторов
и
называется
ЧИСЛО, равное произведению длин этих
векторов на косинус угла между ними:
![]()
Вот это вот уже вполне строгое определение.
Акцентируем внимание на существенной информации:
Обозначение: скалярное
произведение обозначается через ![]() или
просто
или
просто ![]() .
.
Результат операции
является ЧИСЛОМ:
Умножается вектор на вектор, а получается
число. Действительно, если длины
векторов ![]() –
это числа, косинус угла – число, то их
произведение
–
это числа, косинус угла – число, то их
произведение ![]() тоже
будет числом.
тоже
будет числом.
Сразу пара разминочных примеров:
Пример 1
Найти скалярное произведение
векторов
и
,
если ![]()
Решение: Используем
формулу ![]() .
В данном случае:
.
В данном случае:
![]()
Ответ: ![]()
Значения косинуса можно найти в тригонометрической таблице. Рекомендую её распечатать – потребуется практически во всех разделах вышки и потребуется много раз.
Чисто с математической
точки зрения скалярное произведение
безразмерно, то есть результат, в данном
случае ![]() ,
просто число и всё. С точки же зрения
задач физики скалярное произведение
всегда имеет определенный физический
смысл, то есть после результата нужно
указать ту или иную физическую единицу.
Канонический пример по вычислению
работы силы можно найти в любом
учебнике (формула в точности представляет
собой скалярное произведение). Работа
силы измеряется в Джоулях, поэтому, и
ответ запишется вполне конкретно,
например,
,
просто число и всё. С точки же зрения
задач физики скалярное произведение
всегда имеет определенный физический
смысл, то есть после результата нужно
указать ту или иную физическую единицу.
Канонический пример по вычислению
работы силы можно найти в любом
учебнике (формула в точности представляет
собой скалярное произведение). Работа
силы измеряется в Джоулях, поэтому, и
ответ запишется вполне конкретно,
например, ![]() .
.
Пример 2
Найти ![]() ,
если
,
если ![]() ,
а угол между векторами равен
,
а угол между векторами равен ![]() .
.
Это пример для самостоятельного решения, ответ в конце урока.
