19. Определение квадратичной формы

     Квадратичная форма переменных   - функция

 - коэффициенты квадратичной формы. Без ограничения общности считают   тогда

     Если переменные   принимают действительные значения и   квадратичная форма называется действительной.

     Матричная запись квадратичной формы 

     Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если 

     Главные миноры матрицы A называются главными минорами квадратичной формы.

     В пространстве   квадратичную форму можно записать в виде   где X - координатный столбец вектора 

     В пространстве   квадаратичную форму можно представить в виде   где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

 Канонический вид квадратичной формы 

     Квадратичная форма называется канонической, если все   т. е.

     Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

     1. Ортогональное преобразование пространства  :

где   - собственные значения матрицы A.

     2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если 

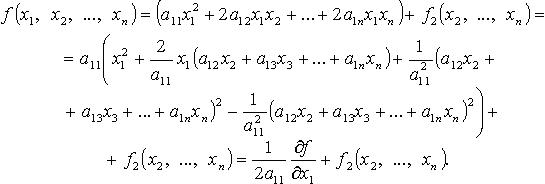
Затем подобную процедуру проделывают с квадратичной формой   и т. д. Если в квадратичной форме все   но есть   то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,   то полагаем     

     3. Метод Якоби (в случае, когда все главные миноры   квадратичной формы отличны от нуля):

Теорема 1. Любая симметричная квадратная матрица порядка n имеет n действительных собственных значений и собственных векторов. Собственные векторы симметричной матрицы попарно ортогональны.

Следовательно, собственные векторы матрицы образуют базис в пространстве  .

Определение 3. Рангом квадратичной формы называется ранг матрицы А.

Определение 4. Квадратичная форма   называется положительно определенной (отрицательно определенной), если для любого   

>0 (<0).

20. Критерий Сильвестра знакоопределенности квадратичной формы. (посмотреть в тетради)

Квадратичная форма является положительно определенной тогда и только тогда, когда все левые верхние угловые миноры матрицы Аявляются положительными, т.е.

,

,

,

.

21. Модель Леонтьева.

2.1. Определение модели и ее продуктивность. Пусть экономика страны (точнее, ее производство) разбита на   отраслей (в реальных моделях   может быть до нескольких сотен). Каждая отрасль вырабатывает лишь один продукт, и каждый продукт производится лишь одной отраслью. При этом для производства продукта некоторой отрасли используются продукты других отраслей.  Рассмотрим выпуск продуктом за некоторый промежуток времени (обычно за год). Пусть через   обозначено количество продукта  -й отрасли, необходимое для выпуска одной единицы продукта   - й отрасли, удельный расход, коэффициент прямых затрат. Важно не перепутать порядок индексов! Числа  , очевидно, неотрицательны:  , и при   образуют квадратную матрицу  размера  . Определение. Матрица   называется технологической матрицей, или матрицей прямых затрат. Неотрицательность   означает неотрицательность матрицы  : 0, где в неравенстве справа написана нулевая матрица размера  . Пусть теперь   – объемы выпуска (производства) продуктов соответственно 1-й, 2-й,…,  -й отраслей , а   – объемы продуктов, оставшихся от  , после того, как их использовали в производствах всех отраслей. Кратко будем называть   выпуском(грязным выпуском), а   – потреблением (чистым выпуском)  - й отрасли.  Выпишем эти соотношения между   и   (балансовые равенства). Всего первого продукта производится  . Из этого количества на производство второго продукта в объеме   уходит  , на производство третьего продукта в объеме   уходит   и т.д. Кроме того, на производство первого же продукта в объеме   уходит   (например, при производстве досок сами же доски используются). Тогда остаток   после производства равен . Аналогично для второго продукта , и так далее. Получаем систему   равенств … (1) Собственно говоря, равенства (1) и есть модель Леонтьева. В дальнейшем проще будет пользоваться матричной записью. Обозначим через   и через   векторы–столбцы выпусков и потребления. Они также должны быть неотрицательными: 0, (2) 0. (3) Кратко в матрично-векторной записи модель Леонтьева можно записать как равенство , (4) или , где   – единичная матрица размера   (на диагонали единицы, остальные – нули).  Если считать вектор потребления   известным, а вектор выпуска   неизвестным, система (4) является квадратной (число уравнений равно числу неизвестных, и равно   ) системой линейных алгебраических уравнений.  Пользуясь понятием «обратная матрица» (матрица, которая после умножения на исходную как справа, так и слева, дает единичную  ) решение системы (4) записывается как , (5)  где  – обратная к  матрица, называемая матрицей полных затрат. С экономической точки зрения модель Леонтьева естественна, когда для любого вектора потребления можно вычислить некоторый вектор выпуска так, чтобы балансовые равенства выполнялись. Это приводит к понятию продуктивность. Определение. Модель Леонтьева называется продуктивной, если для любого вектора (набора) потребления   найдется некоторый вектор выпуска  , удовлетворяющий (4) . Пример 1. Пусть   = 2 (есть всего две отрасли).

Для производства 1 единицы первого продукта необходимо 0.5 единиц этого же первого продукта и 10единиц второго продукта. Для производства 1 единицы второго продукта необходимо 0.1 единиц этого же второго продукта (а первый продукт не нужен).  Пусть необходимо получить для потребления 2 единицы первого продукта ( ) и 5 единиц второго продукта ( ).  Система (1) имеет вид  , или . Решением системы являются значения  .  Если вместо 2 и 5 взять произвольный вектор потребления  , то получим решение   Продуктивность модели очевидна. Заметим, что если взять произвольный неотрицательный выпуск  0, то неотрицательное потребление может и не получиться. Например, если взять в этом примере  , то получим  . Пример 2. «Слегка» исправим пример 1. Пусть

Для производства 1 единицы первого продукта необходимо 10единиц второго продукта. Для производства 1 единицы второго продукта необходимо 0.1 единиц этого же второго продукта и 0.5 единиц первого продукта.  Пусть необходимо получить для потребления 2 единицы первого продукта ( ) и 5 единиц второго продукта ( ).  Система (1) имеет вид  , или . Решением системы являются значения  . Модель непродуктивна. Математически легко доказывается, что Утверждение 1. Если модель продуктивна, то система (4) имеет решение  при любом векторе  , и это решение единственно. Здесь для  ,  не обязаны быть неотрицательными, то есть (2 – 3) может не выполняться. Другими словами, матрица  существует (известно, что многие матрицы не имеют обратной). Утверждение 2. Модель Леонтьева продуктивна тогда и только тогда когда матрица полных затрат неотрицательна: 0. (6) Чтобы это выяснить, нужно  найти. Это легко сделать в EXCEL. Там для этого есть функция (в категории «математические») МОБР. Естественно, предварительно нужно вычислить матрицу . Матрицу   можно найти и в ручную, если знать преобразования Гаусса (см. раздел 3. Методические указания к контрольной работе) В примере 1 

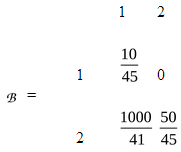Математически также (сложнее) доказывается, что Утверждение 3. Модель Леонтьева продуктивна тогда и только тогда когда матрица полных затрат  может быть представлена в виде ряда:  , (7) что дает представление . (8) Равенство (8) имеет ясную экономическую интерпретацию. Чтобы получить в остатке  , нужно как минимум произвести , а для этого необходимо произвести еще   (прямые затраты для  ). Чтобы произвести эти  , необходимо произвести еще  (прямые затраты для  ) и так далее.  Равенство (7) объясняет, почему  называется матрицей полных затрат. Замечание. Для читателей, имеющих математическое образование, скажем, что равенство (7) справедливо тогда и только тогда когда спектральный радиус матрицы  , то есть максимальный модуль собственных чисел, меньше 1.  ^ 2.2. Разложимость модели Леонтьева. Определение. Группа отраслей   называется изолированной, если продукты всех отраслей, не входящих в  , не используются в производстве продуктов любой отрасли из  (имеется ввиду не используются напрямую). Другими словами, отрасли этой группы могут образовать самостоятельную экономику.  Если такая изолированная группа существует, то соответствующая технологическая матрица называется разложимой.  Так как сказать, что «продукт  -й отрасли не нужен (напрямую) для выпуска продукта   - й отрасли» означает сказать, что  , то равносильное определение выглядит так: Определение. Группа отраслей  (для матриц – группа номеров) называется изолированной, если  для всех , не входящих в   и для всех  , входящих в . Пример 3. Пусть технологическая матрица имеет вид 

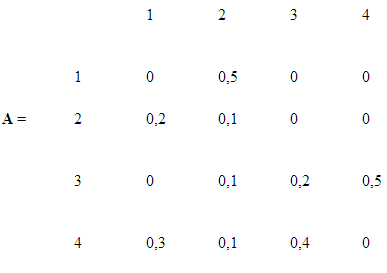Отрасли 3, 4 не нуждаются в продуктах отраслей 1, 2. Группа {3, 4} – изолированная группа.  Несложно показать, что справедливо  Утверждение 4. Для того, чтобы в продуктивной модели не было изолированных групп, необходимо и достаточно, чтобы в матрице полных затрат  не было нулевых элементов, то есть, чтобы  0.  Условие строгой положительности  означает, что продукт  -й отрасли в конце концов (опосредованно, может быть не напрямую) нужен для выпуска продукта   - й отрасли. Это видно из представления (7). Например, для выпуска студентов–очников краска не нужна (напрямую), но нужны какие-либо аудитории, а для аудиторий нужна краска. Тем самым краска все-таки нужна для студентов–очников. Чтобы выяснить наличие изолированной группы отраслей, нужно проанализировать, в каких строчках и столбцах матрицы полных затрат  есть нулевые элементы, а в каких нет.  Но проще и наглядней это сделать, если нарисовать граф, соответствующий матрице .  В графе вершинами являются отрасли (номер вершины = номер отрасли), дуга ( ,  ) из вершины   в вершину   изображается, если  – й продукт нужен для выпуска  -го продукта ), и не изображается, если не нужен, то есть когда  . Если на таком графе из некоторой вершины   в некоторую другую вершину   нет ни одного пути, то есть из нельзя, двигаясь по стрелкам, попасть в  , то изолированные группы точно есть, а отрасль   входит в какую-то изолированную группу.