
- •Задание множеств
- •Сколько студентов не изучает ни одного языка?
- •Операции над множествами
- •Решить систему уравнений
- •Решить систему уравнений
- •Отношения и функции
- •Специальные бинарные отношения
- •Функции алгебры логики
- •Доказать справедливость тождеств:
- •Минимизация булевых функций
- •Элементы комбинаторики
Федеральное агентство по образованию Тверской государственный технический университет
|
|
Дискретная математика Задания на кконтрльную работу
Учебное пособие (для студентов первого курса ИВТ ИДПО)
вычислительные машины, системы, сети и комплексы) |
|
|
|
Тверской государственный технический университет, 2007 |
Оглавление
I. Задание множеств 4
II. Операции над множествами 6
III. Отношения и функции 7
IV. Специальные бинарные отношения 10
V. Функции алгебры логики 11
VI. Минимизация булевых функций 13
VII. Элементы комбинаторики 15
17
Задание множеств
1.Задать перечислением элементов множество :
1.1.{x x=y+z, y,z X, X={1,2}};
1.2. {y y=x+z, x,z X, X={1,3}};
1.3. {y x=y+z, x,z X, X= {1,2}};
1.4. {x x=1 ИЛИ x-2 X, X={1,2}};
1.5. {x x=3 ИЛИ x-3 Y, Y={1,2}};
1. 6.{x x=2 ИЛИ x-2 Z, Z={1,2}}.
2.Найти булеан множества и записать все его компоненты с помощью характеристической функции:
2.1. X = {1,2,3};
2.2. X = {a, b, {a,b}};
2.3. X=;
2.4.X = { ,a,b}.
3. Задать перечислением элементов следующее множество:
3.1. X = { x x=pq, p,q-простые числа, p<5, q<7};
3.2. X = { x x2(x2+2x-8)=0};
3.3. X = { x x2-2x-3=0}.
4. Определить мощность множества:
4.1. , {}, X={x x>5, xN};
4.2.{1,2,3}, {1,{2,3}}, {1,(2,3)}.
Обследование 100 студентов дало следующие результаты о количестве студентов, изучающих различные иностранные языки: испанский - 28, немецкий - 30, французский - 42, испанский и немецкий - 8, испанский и французский - 10, немецкий и французский - 5, все три языка - 3. Используя формулу включений/исключений, определите
сколько студентов не изучает ни одного языка?
сколько студентов изучает один французский язык?
При обследовании 100 студентов, были получены следующие данные о числе студентов, изучающих различные иностранные языки: только немецкий 18, немецкий, но не испанский 23, немецкий и французский 8, немецкий 26, французский 48, французский и испанский 8, никакого языка 24. Используя формулу включений/исключений, определите
Сколько студентов не изучает ни одного языка?
сколько студентов изучают испанский язык?
сколько студентов изучают немецкий и испанский языки, но не французский?
В отчете об обследовании 100 студентов, изучающих иностранные языки (См. задание 5), указывалось, что количество студентов, изучающих различные языки таково: все три языка 5, немецкий и испанский 10, французский и испанский 8, немецкий и французский 20, испанский 30, немецкий 23, французский 50. Инспектор, представивший этот отчет, был уволен. Почему? При обосновании ответа используйте формулу включений/исключений.
Известно, что из 100 студентов живописью увлекается 28, спортом - 42, музыкой - 30, живописью и спортом - 10, живописью и музыкой - 8, спортом и музыкой - 5, живописью, спортом и музыкой - 3. Используя формулу включений/исключений, определите
сколько студентов увлекается только спортом;
сколько студентов увлекается только живописью;
сколько студентов увлекается только музыкой;
определить число студентов, не увлекающихся ничем.
Пусть I = { a,b,c,d,e,f }, X = { a,b,c }, Y = {a,c,e,f }, Z = { d,e }. Определить множество, заданное формулой, перечислением элементов и с помощью характеристической функции:
X\(YZ).
(Х Z)\Y;
( X (Y Z));
(X Y) (X Z));
 ;
;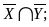
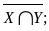
(X Y) Z;
X (Y Z);
X\Z;
X\Z Y\Z.
Справедливо ли утверждение : = { }?
Справедливо ли высказывание: если А В и В С, то А С? Привести примеры.
Пусть А, В,С - множества и С В. Доказать, что А С А В.
Пусть С и D не пустые произвольные множества. Определить C D и C D.
Какие из следующих утверждений справедливы:
0 ;
= {0};
{ }=1;
{{ }}={{{}}};
{{}}=2;
{};
{};
I;
{}{{}}.
