106. Интегральный признак Коши

Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на  , последний часто может быть найден в явном виде.

Формулировка теоремы Пусть для функции f(x) выполняется:

1.  (функция принимает неотрицательные значения)

2.  (функция монотонно убывает)

3.  (соответствие функции ряду)

Тогда ряд   и несобственный интеграл   сходятся или расходятся одновременно.

107 Признак Раабе Признак Раабе (признак Раабе — Дюамеля) — признак сходимости знакоположительных числовых рядов, Формулировка Теоремы

Ряд   сходится, если при достаточно больших   выполняется неравенство

где  .

Eсли  , начиная с некоторого  , то ряд   расходится. В предельной форме Если существует предел:

то при   ряд сходится, а при   — расходится.

Замечание. Если  , то признак Раабе не даёт ответа на вопрос о сходимости ряда

108. Признак Гаусса

Признак Гаусса — общий признак сходимости числовых рядов с положительными членами,

Формулировка Пусть дан ряд   и ограниченная числовая последовательность  . Тогда если отношение   представимо в виде:

где   — постоянные числа ( ), то ряд   сходится при   и расходится при  . Если же  , то ряд сходится при   и расходится при 

109 . Теорема об абсолютной сходимости

Ряд   называют абсолютно сходящимся числовым рядом, если сходится ряд  .

из сходимости ряда   вытекает сходимость ряда  .

При исследовании абсолютной сходимости ряда используют признаки сходимости рядов с положительными членами.

Если ряд   расходится, то для выявления условной сходимости числового ряда используют более тонкие признаки: Признак Лейбница, признак Абеля, признак Дирихле.

110. Признак Лейбница

Признак Лейбница

Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:

Пусть для знакочередующегося ряда выполняются следующие условия:  (монотонное убывание {an})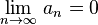 . Тогда этот ряд сходится.

Замечания:

Если, выполнены все условия, и ряд из модулей ( ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность   существенна.

Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.

Пример

. Ряд из модулей имеет вид   — это гармонический ряд, который расходится.

Теперь воспользуемся признаком Лейбница:

1. знакочередование выполнено 

2. 

3. .

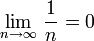Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.

Оценка остатка ряда Лейбница

Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена ряда. Поскольку любой остаток ряда r_n является также рядом Лейбница, то для него справедливо:

.