Моменты инерции твердого тела относительно оси и полюса. Радиус инерции. Теорема о моментах инерции относительно параллельных осей. Осевые моменты инерции некоторых однородных тел.
Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:
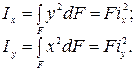
Ввели в рассмотрение еще две геометрические характеристики: радиусы инерции поперечного сечения относительно осей x и y, соответственно. Формула радиуса инерции имеет вид:
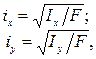
Главным центральным осям инерции соответствуют главные радиусы инерции:
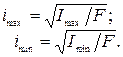
Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:
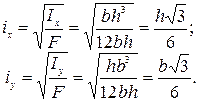
Для круглого сечения формула главных радиусов инерции имеет вид:
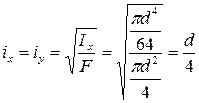
Количество движения точки. Элементарный и полный импульс силы. Количество движения механической системы. Теоремы об изменении количества движения точки и механической системы.
Теорема об изменении кинетической энергии м.С.
Формулируется эта теорема практически так же, как и теорема об изменении кинетической энергии материальной точки. Только с учетом деления сил, действующих на каждую точку в системе, на внешние и внутренние.
Изменение кинетической энергии механической системы на некотором ее перемещении
равно сумме работ внешних и внутренних сил, приложенных к точкам системы,
на том же перемещении.
Доказывается теорема, естественно, аналогично остальным. То есть записывается теорема об изменении кинетической энергии каждой из точек системы под действием внешних и внутренних сил, а затем все уравнения складываются.
Это возможно, если в системе тел имеются упругие элементы. Например, колебания на гладкой горизонтальной поверхности двух соединенных между собой пружиной шариков. Это может быть и в том случае, если между деталями рассматриваемых механизмов существует внутреннее трение.
Необходимо отметить, что при решении учебных задач системы с упругими элементами практически не встречаются, а внутренним трением в шарнирах, соединяющих детали механизмов, авторы задач, как правило, советуют пренебречь. Поэтому при решении типовых задач рассматриваемую теорему автор рекомендует записывать и формулировать для себя несколько короче:
*** В параграфе, посвященном определению работы различных сил, доказывается, что работа внутренних сил, приложенных к точкам твердых тел, на любых их перемещениях равна нулю.
При решении задач обычно используется интегральная форма теоремы. С ее помощью определяется изменение скоростей точек системы на некотором перемещении под действием известных сил. Но возможно и решение иных задач. В некоторых случаях по определенному опытным путем изменению скорости тела или системы тел судят о работе сил сопротивления среды или каких-то других сил.
В дифференциальной форме теорему обычно применяют для определения ускорений точек системы в рассматриваемом положении.
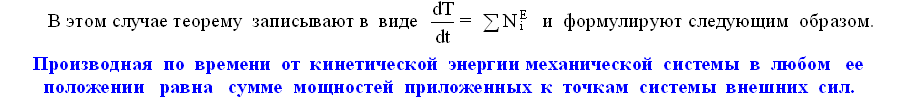
О решении задач с помощью рассматриваемой теоремы и остальных общих теорем динамики для механических систем речь пойдет отдельно. Закончим же теорему об изменении кинетической энергии М.С. формулировкой следующего закона сохранения.
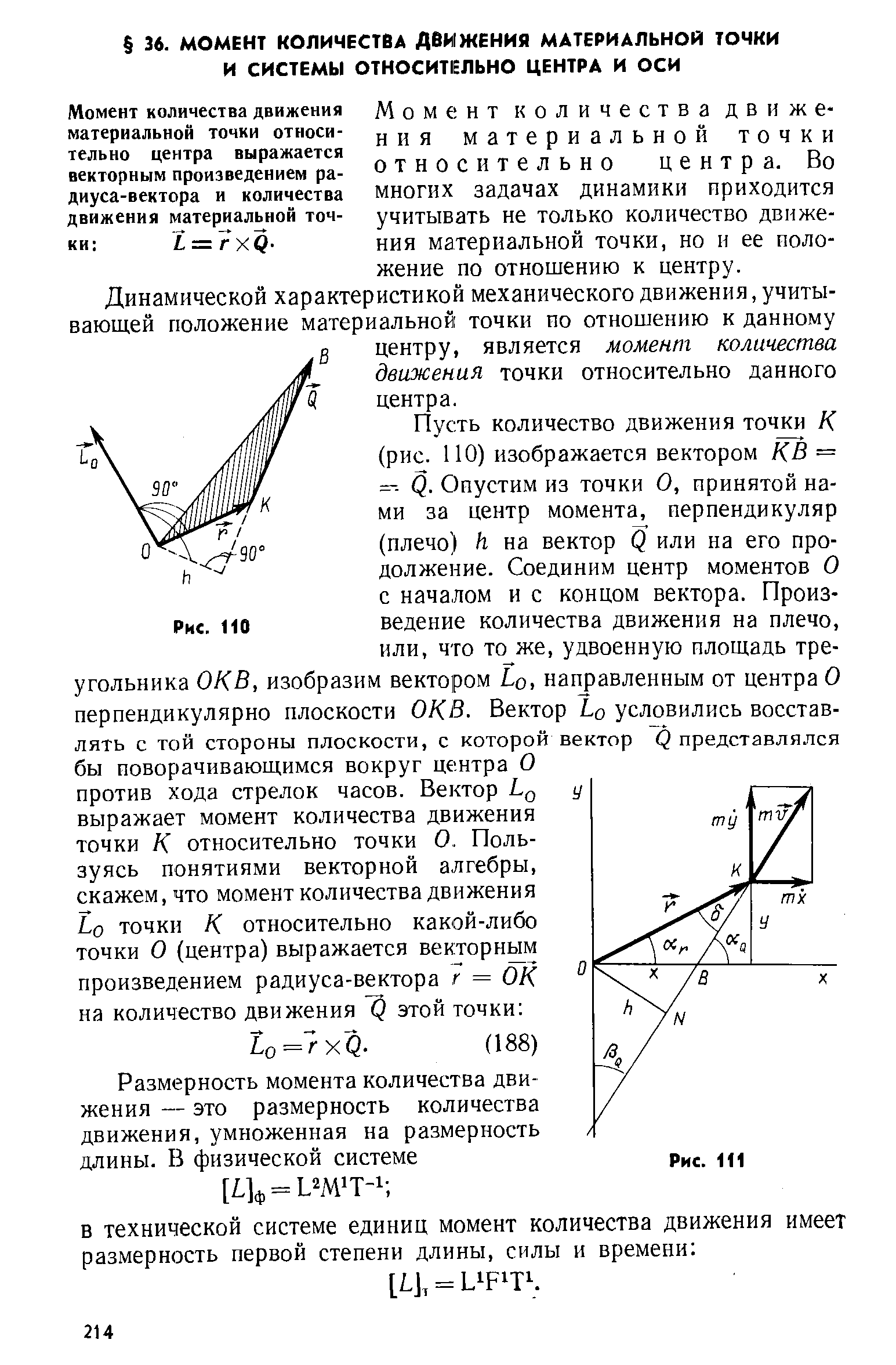
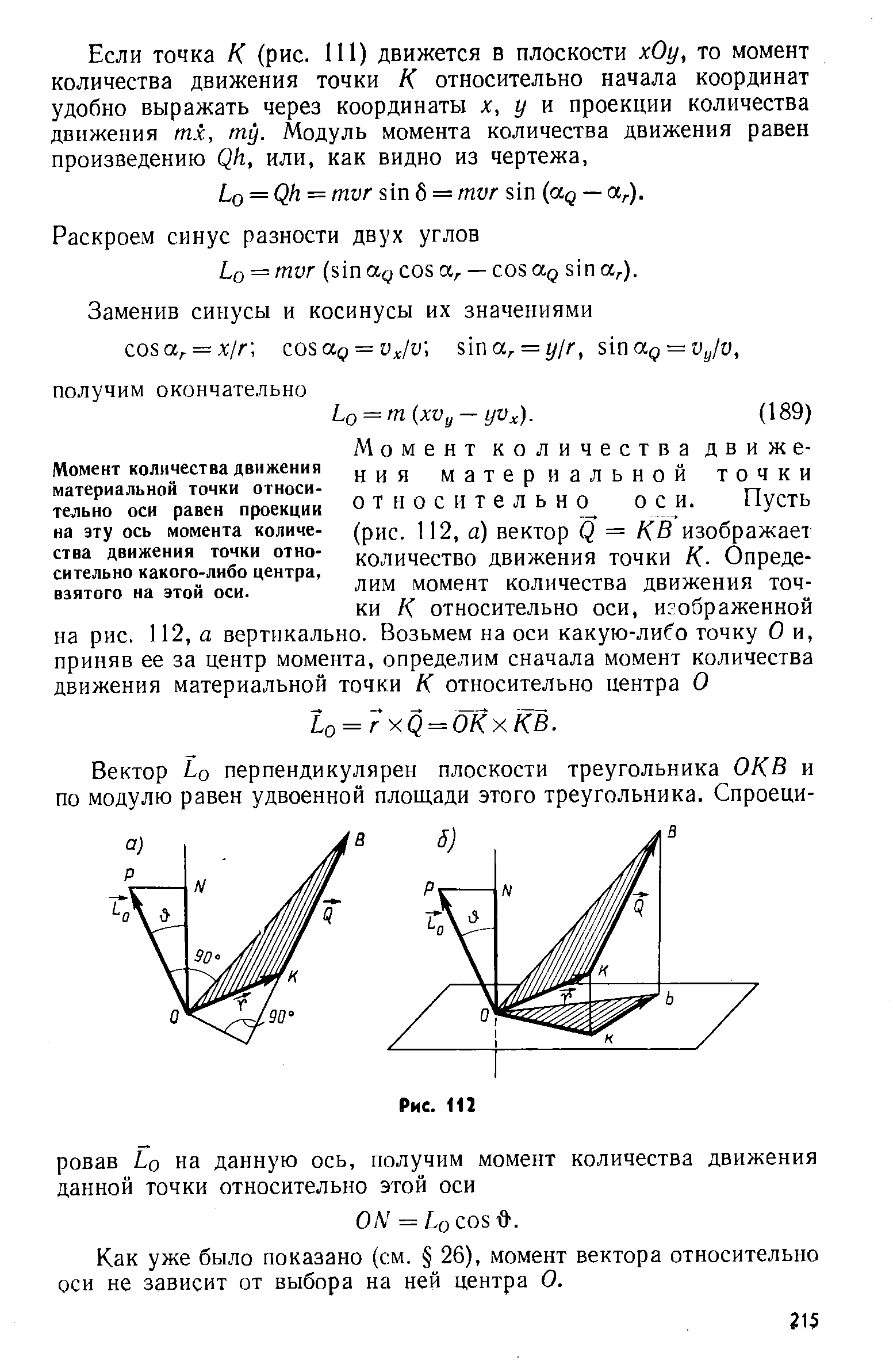
Момент количества движения точки относительно центра и оси. Главный момент количеств движения. Теорема об изменении момента количества движении точки.
