29. Определение ускорений точек тела.

 Мгновенный центр ускорений (МЦУ). Способы нахождения.

При определении скоростей точек плоской фигуры было установлено, что в каждый момент времени существует такая точка Р фигуры (МЦС), скорость которой равна нулю. Покажем, что в каждый момент времени существует точка фигуры, ускорение которой равно нулю. Такая точка называется мгновенным центром ускорений (МЦУ). Обозначим ее через Q.

Рассмотрим плоскую фигуру, совершающую движение в плоскости рисунка (рис.). Примем за полюс какую-либо точку А, модуль и направление ускорения аА которой известны в рассматриваемый момент времени. Пусть в этот момент времени известны угловая скорость и угловое ускорение фигуры. Из формулы   следует, что точка Q будет МЦУ, если  , т. е. когда  . Так как вектор aQA составляет с линией AQ угол "альфа"  , то параллельный ему вектор аА направлен к линии, соединяющей полюс А с точкой Q, также под углом "альфа" (см. рис.).

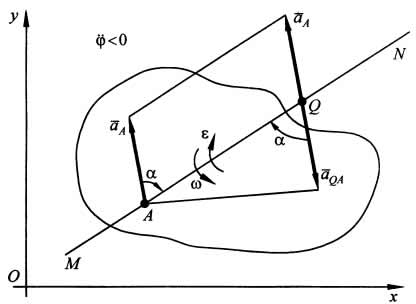
Проведем через полюс А прямую MN, составляющую с вектором его ускорения угол "альфа", откладываемый от вектора аА в направлении дуговой стрелки углового ускорения. Тогда на луче AN найдется точка Q, для которой  . Поскольку, согласно  ,  , точка Q (МЦУ) будет отстоять от полюса А на расстоянии  .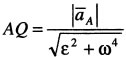

Таким образом, в каждый момент движения плоской фигуры, если угловая скорость и угловое ускорение не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. В каждый последующий момент времени МЦУ плоской фигуры будет находиться в различных ее точках.

Если МЦУ — точку Q выбрать за полюс, то ускорение любой точки А плоской фигуры , так как aQ = 0. Тогда  . Ускорение аА составляет с отрезком QA, соединяющим эту точку с МЦУ, угол "альфа", откладываемый от QA в сторону, противоположную направлению дуговой стрелки углового ускорения. Ускорения точек фигуры при плоском движении пропорциональны расстояниям от МЦУ до этих точек.

Таким образом, ускорение всякой точки фигуры при ее плоском движении определяется в данный момент времени так же, как и при вращательном движении фигуры вокруг МЦУ.

Рассмотрим случаи, когда положение МЦУ можно определить с помощью геометрических построений.

30. Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела.

Векторное представление угловой скорости и углового ускорения тела позволяют записать линейную скорость, а также касательное и нормальное ускорения произвольной точки тела в виде следующих векторных произведений:

В этих формулах (омега и эбселент) - векторы угловой скорости и углового ускорения тела, приложенные в произвольной точке О оси вращения, г - радиус-вектор рассматриваемой точки, проведенный из точки О (рис. 96). Справедливость формул проверяется непосредственно.

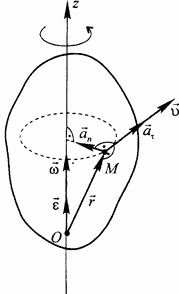
Рис. 96.

Формулы широко используются при изучении кинематики более общих случаев движения твердого тела.

31. Относительное, переносное и абсолютное движение точки

Сложным движением точки называется такое ее движение, при кото­ром она движется относительно системы отсчета, перемещающейся по отношению к некоторой другой системе отсчета, принятой за непод­вижную. Например, можно считать, что пассажир, идущий по вагону движущегося поезда, со­вершает сложное движение по отношению к полотну дороги, состоящее из движения пассажира по отношению к вагону (подвижная система отсчета) и дви­жения пассажира вместе с вагоном по отношению к полотну дороги (неподвижная система отсчета).

Движение точки по отношению к подвижной системе ко­ординат называется относительным движением точки. Скорость и ускорение этого движения называют относитель­ной скоростью иотносительным ускорением и обозначают    и  .

Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки.

Переносной скоростью и переносным ускорением точки на­зывают скорость и ускорение той, жестко связанной с под­вижной системой коор­динат точки, с которой совпадает в дан­ный момент времени движущаяся точка, и обозначают    и  .

Движение точки по отношению к неподвижной системе координат называ­ется абсолютнымили сложным. Скорость и ускорение точки в этом движении называют абсолютной скоростью иабсолютным ускорением и обозначают    и  .

В приведенном выше примере движение пассажира относительно вагона будет относительным, а скорость – относительной скоростью пассажира; движение вагона по отношению к полотну дороги будет для пассажира переносным движением, а скорость вагона, в котором находится пассажир, будет в этот момент его переносной скоростью; наконец, движение пассажира по отношению к полотну будет его абсолютным движением, а скорость – абсолютной скоростью.