3 Основы микромеханики двухкомпонентных

СИСТЕМ

3.1 Определение упругих характеристик однонаправленного слоя

3.1.1 Основные предпосылки

Изучение механического поведения композиционных материалов проводится на двух уровнях абстрагирования. Первый уровень, называемый микромеханикой, включает тонкие детали структуры композита на уровне размеров волокна, которое помещено в матрицу [1, 7, 19]. Таким образом, микромеханика не подразумевает исследований на атомном уровне. Главная задача микромеханики - связать эффективные модули упругости композита со свойствами его компонентов.

Основным результатом решения задачи в микромеханической постановке является вычисление эффективных модулей однонаправленного слоя, которые определяются как коэффициенты, связывающие усредненные по объему значения напряжений (компонент тензора напряжений) и деформаций (компонент тензора деформаций) при определенных граничных условиях.

Рассматриваемый ниже подход к вычислению эффективных модулей композиционных материалов основан на понятии представительного элемента объема, т. е. такого элемента, в котором все усредненные по объему компоненты напряжений и деформаций равны соответствующим величинам, вычисленным для рассматриваемого композита в целом. Как правило, микромеханика ограничивается вычислением эффективных модулей упругости и коэффициентов Пуассона однонаправленного композиционного слоя. Эти вычисления дают возможность дальнейшего аналитического исследования на новом уровне абстрагирования, а именно на уровне слоистого тела. При этом реальный неоднородный материал рассматривается как однородное анизотропное тело, состоящее из однонаправленных слоев, ориентированных под разными углами (рис. 3.1).

Слой - основной элемент в композите, состоящий из погруженных в матрицу однонаправленных волокон. Следовательно, можно связать упругие и прочностные свойства однонаправленного слоя с соответствующими свойствами компонентов. Таким образом, имеется возможность проектировать элементы конструкций из волокнистых композитов, зная конструктивные требования к конструкции и свойства компонентов композитов.

Рис. 3.1 Волокнистый композит с укладкой слоев:

90, - , + , 0

При определении упругих постоянных однонаправленного слоя по известным упругим характеристикам волокон и связующего необходимо рассмотреть напряженно-деформированное состояние последних при нагружении слоя вдоль армирования, поперек и при сдвиге. Совместная работа волокна и связующего, обладающих различными упругими характеристиками, представляет собой сложную математическую задачу. Для определения напряжений и деформаций в компонентах композиционного материала используют физические и математические модели, как самих компонентов, так и модели их совместной работы.

Для упрощения расчетов вводится ряд допущений:

1. Компоненты композиционного материала являются однородными и линейно - упругими материалами.

2. Связующее является изотропным, а волокна могут быть изотропными или трансверсально-изотропными.

3. Армирующие волокна являются прямыми и параллельными.

4. Армирующие волокна распределены равномерно и имеют одинаковое сечение.

Сама модель совместной их работы предполагает, что между арматурой и связующим существует жесткое сцепление, т. е. отсутствует скольжение. Поры как в арматуре, связующем, так и на поверхности их раздела отсутствуют.

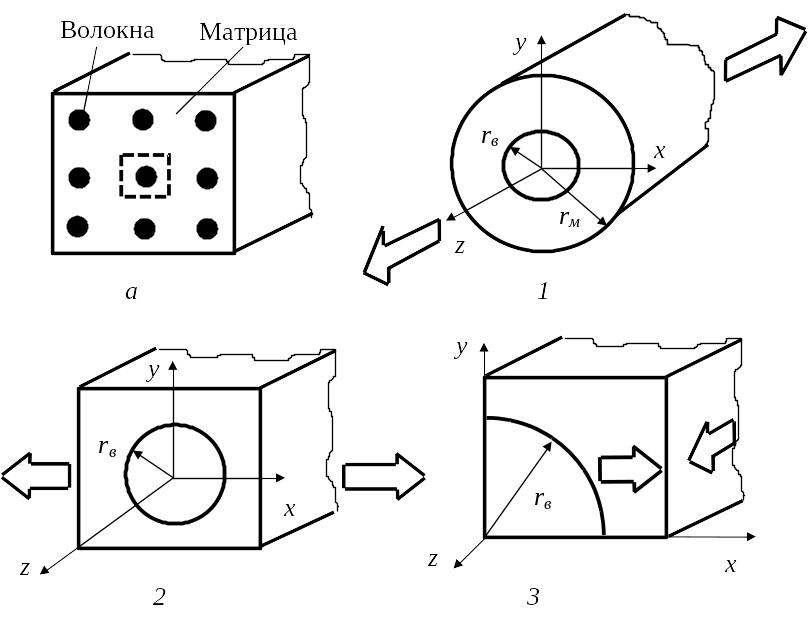
Для определения напряжений в компонентах однонаправленного слоя в качестве расчетной модели будем пользоваться повторяющимся элементом структуры материала. Периодически повторяющийся элемент представляет собой типичную модель, применяемую в микромеханике для определения механических свойств композитов. На рис. 3.2 показаны модели, которые используются в работе [26] для определения упругих свойств композитов на основе методов сопротивления материалов.

В этой модели выделяются три элемента: первый - для определения поля внутренних напряжений при нагружении вдоль волокон, второй - для определения напряжений при нагружении поперек волокон, третий - для определения напряжений при сдвиге. Определение поля внутренних напряжений в волокне и связующем при различных видах нагружения представляет большие математические трудности. В инженерных расчетах, как правило, используют упрощенные модели, базирующиеся на методах сопротивления материалов. Полученные решения сопоставляются, где это возможно, с решениями, полученными на более точных моделях. Эти модели и решения изложены в целом ряде монографий и статей [ 19, 26, 28, 33 и др.].

Рис. 3.2 Представительный объем композитного материала (а)

и повторяющиеся элементы однонаправленного слоя для

определения:

1 - продольного модуля упругости; 2 - поперечного модуля;

3 - модуля сдвига

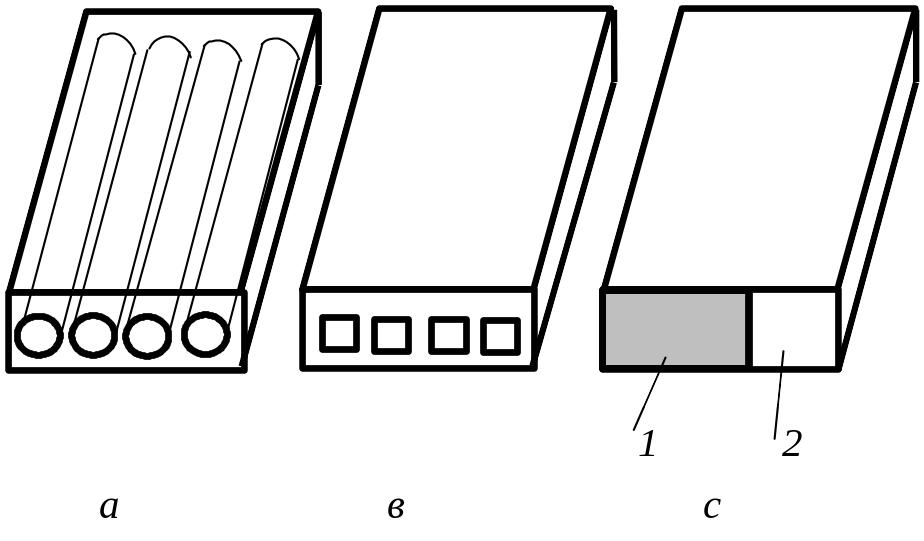
В качестве упрощенной модели используется однонаправленный слой, состоящий из объема, занятого армирующими волокнами, и объема, занятого матрицей (рис. 3.3, в).

Возможность в этой модели пренебречь влиянием коэффициентов Пуассона волокна и матрицы, геометрической формой поперечного сечения армирующих волокон при определении эффективных модулей упругости однонаправленного слоя позволяет существенно упростить решения.

Рис. 3.3 Модели однонаправленного слоя с круглыми (а) и

эквивалентными им по площади прямоугольными волокнами (в);

с – упрощенная модель однонаправленного слоя для

определения упругих свойств:

1 – объем, занятый волокном; 2 – объем, занятый матрицей