Лекция 3 (сокращенный вариант)
Основные понятия и формулы электрического тока и магнитостатики
3.1. Математическое описание законов электрического тока
Пусть имеется
некоторый объем
,
охваченный поверхностью
,
через которую движутся заряды, рис. 3.1.
Рис. 3.1. Объем , из которого течет ток
Тогда силой тока
назовем скорость уменьшения зарядов
в объеме
.
(3.1)
Величина силы тока является положительной, т.к. скорость убывания как соответствующая производная убывающей функции – отрицательна.
Поток
плотности тока
через
площадку
определяется скалярным произведением:
.
По абсолютной величине плотность тока
(3.2)
равна току, отнесенному к единичной площади, расположенной перпендикулярно направлению движения зарядов.
Полный ток
– это поток вектора
через поверхность
.
(3.3)
Выразим
через объемную плотность заряда
,
.
Тогда ток, вытекающий из объема , равен потоку вектора через поверхность , охватывающему этот объем,
.
С другой стороны по теореме Гаусса-Остроградского
.
(3.4)
Следовательно
.
(3.5)
Это означает, что
ток и его линии зарождаются там, где
плотность заряда меняется во времени.
Там, где
,
и
.
(3.6)
Условие означает постоянство тока и непрерывность его линий. Левое равенство (3.6) также означает отсутствие истоков или стоков, т.е. непрерывность и замкнутость контура движения постоянного тока, поскольку отсутствуют области его дополнительного возникновения или исчезновения. Правое равенство составляет содержание первого закона Кирхгофа. Это равенство не утверждает, что ток в проводнике отсутствует. Оно лишь говорит о том, что количество втекающего тока в объем равно количеству вытекающего из него тока.
Закон Ома
В дифференциальной форме закон Ома формулируется так:
,
(3.7)
где
– удельная электропроводность среды.
В интегральной форме закон Ома имеет вид:
,
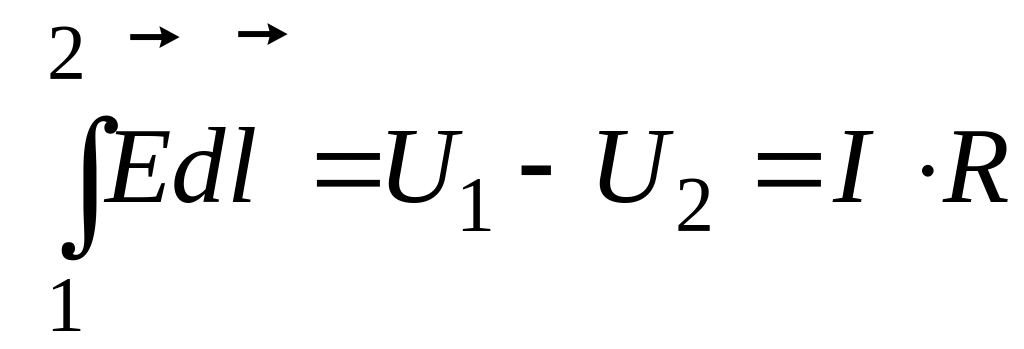(3.8)
где
–
работа
поля,
выполняемая
при перемещении единичного
заряда
в проводнике
от
его поперечного сечения
до
;
-сопротивление
проводника;
– разность потенциалов в соответствующих
точках.