Простой силлогизм

Рассмотренные в предыдущей лекции дедуктивные умозаключения также называются силлогизмами. Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все суждения, входящие в него (две посылки и вывод), являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма.

Все цветы (М) – это растения (Р). Все розы (S) – это цветы (М).

Все розы (S) – это растения (Р).

Обе посылки и вывод являются в данном силлогизме простыми суждениями, причем и посылки, и вывод – это суждения вида А (общеутвердительные). Обратим внимание на вывод, представленный суждением: Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы возможно связать в выводе. Таким образом, структура силлогизма включает две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родо-видового подчинения, в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.

3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М.

Фигуры простого силлогизма

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т.е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы (М) – это химические элементы (Р). Гелий (S) – это газ (М).

Гелий (S) – это химический элемент (Р).

У читывая то, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере.

Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре.

Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

Все рыбы (Р) дышат жабрами (М). Все киты (S) не дышат жабрами (М).

Все киты (S) не рыбы (Р).·

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так

Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры (М) – это млекопитающие (Р). Все тигры (М) – это хищники (S).

Некоторые хищники (S) – это млекопитающие (Р).

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма.

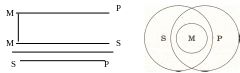
Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

Все квадраты (Р) – это прямоугольники (М). Все прямоугольники (М) – это не треугольники (S).

Все треугольники (S) – это не квадраты (Р).

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма.