4. Процессы гибели и размножения. Уравнения Чепмена-Колмогорова.

Процессом гибели и размножения (ПГР) называют однородную непрерывную цепь Маркова, в которой переходы разрешены только в соседние состояния. Свяжем с каждым состоянием i ПГР вероятность p_i(t)=P(X(t)=i) – вероятность того, что в момент времени t процесс будет находиться в соcтоянии i.

p₀(t) p₁(t) p₂(t) p₃(t) p_n(t) p_n+1(t)

Поскольку из узла 0 выходит дуга с интенсивностью , а в него входит из узла 1 дуга с интенсивностью , то имеет место дифференциальное уравнение: .

Для узла 1 аналогичное уравнение будет иметь вид: Обобщая, для узла n получим: .

Таким образом, для ПГР имеет место система дифференциальных уравнений

(1)

Система дифференциальных уравнений (1) называется системой уравнений Чепмена-Колмогорова для ПГР. Ее отличительная особенность – бесконечное число уравнений. Решение ее без знания специальных разделов высшей математики невозможно. Поэтому оставляем его за пределами нашего рассмотрения.

4. Процесс чистого размножения (гибели). Процесс чистого размножения. Рассмотрим процесс гибели и размножения, для которого интенсивность размножения постоянна (не зависит от состояния) и равна λ, т.е. λ₀= λ₁= …= λ_n-1= λ_n=…=λ. Интенсивность гибели в любом состоянии равна 0: μ₀= μ ₁= …= μ _n-1= μ _n=…=0.

Такой процесс называется процессом чистого размножения. С точки зрения СМО он описывает процесс поступления заявок в систему с постоянной интенсивностью. Процессу чистого размножения соответствует диаграмма

p₀(t) p₁(t) p₂(t) p₃(t) p_n(t) p_n+1(t)

Система уравнений Чепмена-Колмогорова для процесса чистого размножения принимает вид:

(2)

О говорим начальные условия. Допустим, что в начальный момент процесс находится в состоянии 0, т.е. p₀(0)=1, p_i(0)=0, i=1,2, …, n, … (3)

Найти решение системы (2), (3) не представляет труда. Действительно, первое уравнение системы с соответствующим начальным условием дает очень простую задачу Коши: .

Дифференциальное уравнение в задаче – простейшее дифференциальное уравнение 1-го порядка с постоянными коэффициентами, которое имеет общее решение p₀(t)=Ce^-λt. Постоянная интегрирования C находится из начального условия: p₀(0)=Ce⁰=1. Следовательно C=1 и

p₀(t)=e^-λt. (4)

Для узла 1 система (2), (3) дает задачу Коши:

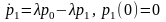. (5)

Подставив (4) в (5) получим

(6)

Решив (6), найдем p₁(t)= (λt) e^-λt.

Рассматривая далее узлы 2, 3, …, n, …по аналогии получим

Р ассмотрим процесс чистого размножения как процесс поступления заявок в СМО. Пусть τ – интервал времени между двумя последовательно поступающими в систему заявками. Как отмечалось ранее, τ – случайная величина, A(t)=P(τ<t) – функция распределения этой величины. Сравним A(t) и p₀(t). p₀(t) – это вероятность того, что в момент времени t процесс будет находится в состоянии 0. Поскольку рассматриваемый процесс есть процесс чистого размножения, то это означает, что на промежутке [0,t] в СМО не поступит ни одной заявки, т.е. p₀(t)=P(τ≥t)=1- P(τ<t)=1-A(t).

Из последнего равенства вытекает, что A(t)=1- p₀(t)=1- e^-λt. (7)

Снова напомним, что A(t) – функция распределения случайной величины τ. Закон распределения, определяемый соотношением (7), называется в теории вероятностей показательным. Следовательно, если процесс поступления заявок в СМО обладает свойствами процесса чистого размножения, то интервалы времени между поступающими заявками распределены по показательному закону.

В теории случайных процессов доказано и обратное: если интервалы времени между поступающими в СМО заявками распределены по показательному закону, то процесс поступления заявок в СМО представляет из себя процесс чистого размножения.

Процесс чистой гибели. Аналогично процессу чистого размножения рассмотрим процесс чистой гибели, который получается из обычного ПГР при следующих условиях: λ₀= λ₁= …= λ_n-1= λ_n=…=0,

μ₀= μ ₁= …= μ _n-1= μ _n=…= μ.

По аналогии с п.2, можно показать, что если интерпретировать процесс чистой гибели, как процесс обслуживания заявок в СМО, то интервалы времени обслуживания заявок (в принятых нами обозначениях – случайная величина x) будут распределены по показательному закону B(t)= 1- e^-μt. (8)

Верно и обратное: если интервалы времени обслуживания распределены по показательному закону (8), то процесс обслуживания заявок СМО будет представлять собой процесс чистой гибели.

4. Системы массового обслуживания: связь с процессами гибели и размножения. Очевидна интерпретация ПГР и с точки зрения СМО. Рождение – это поступление новой заявки в систему. Гибель – выход из системы обслуженной заявки. Состояние ПГР – количество заявок, находящихся в системе. Существует другое определение процесса гибели и размножения. Это случайный процесс, для которого

1. Вероятность рождения одного и только одного нового члена популяции на промежутке времени пропорциональна длительности этого промежутка и составляет , где - бесконечно малая величина от ;

2. Вероятность того, что на интервале не родится ни одного нового члена популяции составляет ;

3. Вероятность гибели ровно одного члена популяции на интервале пропорциональна длительности этого промежутка и составляет ;

4. Вероятность того, что на этом промежутке не произойдет ни одной гибели определяется соотношением

Свойства 1-4 обуславливают невозможность как одновременного появления, так и одновременной гибели двух и более особей популяции.

В теории случайных процессов доказано, что оба определения процесса гибели и размножения эквивалентны.

ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ, МОДЕЛИ И ФОРМУЛЫ

1. Какие модели относят к динамическому программированию?

2. Сформулируйте принцип инвариантного погружения.

3. Сформулируйте принцип оптимальности.

4. Запишите математическую модель задачи о распределении ресурсов.

5. В чем состоит принцип инвариантного погружения для задачи о распределении ресурсов?

6. Что выражает функция Беллмана в задаче о распределении ресурсов?

7. Запишите рекуррентные соотношения Беллмана для задачи о распределении ресурсов.

8. Сформулируйте задачу о замене оборудования.

9. Что выражает функция Беллмана в задаче о замене оборудования?

10. Запишите рекуррентные соотношения Беллмана для задачи о замене оборудования.

11. Запишите задачу математического программирования в общей форме.

12. Дайте определение унимодальной функции.

13. Какая идея лежит в основе методов сечений для отыскания экстремума унимодальной функции?

14. Что такое линия уровня функции n переменных?

15. Что такое градиент функции n переменных?

16. Как располагаются в пространстве градиент и касательная поверхность (плоскость, прямая) к линии уровня?

17. Что такое «направления спуска»?

18. Нарисуйте геометрическую интерпретацию метода наискорейшего спуска.

19. Нарисуйте геометрическую интерпретацию метода покоординатного спуска.

20. На какой идее основан метод штрафных функций?

21. На какой идее основан метод барьерных функций?

22. Дайте определение системе массового обслуживания (СМО)? Почему конвеер не является СМО?

23. Какая случайная величина используется для описания входного потока заявок?

24. Какая случайная величина используется для описания процесса обслуживания?

25. Какая СМО называется элементарной? Неэлементарной?

26. Какие основные факторы используются при классификации СМО?

27. Охарактеризуйте СМО типа M/M/1.

28. Охарактеризуйте СМО типа M/M/∞.

29. Охарактеризуйте СМО типа M/M/m.

30. Охарактеризуйте СМО типа M/M/m/k.

31. Охарактеризуйте СМО типа G/Er/m/k.

32. Что такое случайный процесс (СП)?

33. Какие факторы используются для классификации СП.

34. Какой СП называется стационарным?

35. Какой СП называется марковским?

36. Какой СП называется полумарковским?

37. Какой СП называется процессом гибели и размножения?

38. Дайте определение дискретной цепи Маркова (ДЦМ).

39. Что называется переходной вероятностью за 1 шаг? За k шагов?

40. Какая ДЦМ называется однородной?

41. Запишите уравнение Чепмена-Колмогорова для однородной ДЦМ (ОДЦМ).

42. Что такое «вектор распределения вероятностей состояний» для ОДЦМ?

43. Как связаны векторы распределение вероятностей состояние на k-ом и (k+1)-ом шагах.

44. Что такое «предельное распределение вероятностей» ОДЦМ?

45. Что такое «стационарное распределение вероятностей» ОДЦМ?

46. Как найти стационарное распределение вероятностей точно?

47. Как найти стационарное распределение вероятностей приближенно? – нет ответа

48. По какому закону распределено время пребывания ОДЦМ в одном и том же состоянии. Запишите формулу, характеризующую данное распределение.

49. Дайте определение непрерывной цепи Маркова (НЦП).

50. Что такое «переходная вероятность» на заданном промежутке времени (для НЦП)?

51. Какая НЦМ называется однородной? Как определяется переходная вероятность для однородной НЦМ (ОНЦП)?

52. Запишите уравнение Чепмена-Колмогорова для ОНЦМ.

53. Что такое «распределение вероятностей состояний» для ОНЦМ?

54. Запишите матричное дифференциальное уравнение, которому удовлетворяет распределение вероятностей состояний ОНЦМ.

55. Что такое «предельное распределение вероятностей» для ОНЦМ?

56. Что такое «стационарное распределение вероятностей» для ОНЦМ?

57. Как найти стационарное распределение вероятностей состояний для ОНЦМ?

58. Что такое «процесс гибели и размножения (ПГиР)»?

59. Нарисуйте диаграмму переходов для ПГиР.

60. Что такое процесс «чистого» размножения? Нарисуйте диаграмму переходов процесса «чистого» размножения.

61. Что такое процесс «чистой» гибели? Нарисуйте диаграмму переходов процесса «чистой» гибели.

62. Опишите связь между ПГиР и СМО.

КОМПЛЕКСНЫЕ ВОПРОСЫ

1. Динамическое программирование: предмет исследования, математическая модель многошагового процесса.

2. Задача распределения ресурсов: постановка и анализ (вывод соотношений Беллмана).

3. Задача о замене оборудования: постановка и анализ (вывод соотношений Беллмана))

4. Математическое программирование: предмет исследования, общие сведения о численных методах отыскания экстремумов.

5. Метод множителей Лагранжа.

6. Численные методы: общая характеристика методов отыскания экстремума функции одной переменной.

7. Численные методы одномерной минимизации: метод «золотого» сечения.

8. Численные методы одномерной минимизации: метод квадратичной интерполяции.

9. Численные методы одномерной минимизации: методы первого и второго порядка.

10. Отыскание экстремума функции n переменных. Градиент, линия уровня, их свойства.

11. Отыскание экстремума функции n переменных. Общая схема методов спуска.

12. Методы наискорейшего и покоординатного спуска для отыскания экстремума функции n переменных.

13. Решение задач математического программирования путем сведения их к задачам безусловного экстремума. Метод штрафных функций.

14. Решение задач математического программирования путем сведения их к задачам безусловного экстремума. Метод барьерных функций.

15. Понятие системы массового обслуживания (СМО). Структура СМО, классификация.

16. Понятие случайного процесса, классификация.

17. Дискретные цепи Маркова: определение, матрица переходных вероятностей, уравнение Чепмена-Колмогорова.

18. Дискретные цепи Маркова: стационарное распределение вероятностей.

19. Дискретные цепи Маркова: распределение времени пребывания в одном и том же состоянии.

20. Непрерывные цепи Маркова: определение, уравнение Чепмена-Колмогорова.

21. Непрерывные цепи Маркова: стационарное распределение вероятностей.

22. Процессы гибели и размножения. Уравнения Чепмена-Колмогорова.

23. Процесс чистого размножения (гибели).

24. Системы массового обслуживания: связь с процессами гибели и размножения.