4. Дискретные цепи Маркова: определение, матрица переходных вероятностей, уравнение Чепмена-Колмогорова.

Дискретной цепью Маркова будем называть последовательность случайных величин, принимающих значение из множества х={0, 1, 2,…, n,…} и обладающих свойством Маркова: Р(x_k+1=x_k+1| x_k=i_k, x_k-1=i_k-1,,…x₀=i₀)=P(x_k+1=i_k+1| x_k=i_k)

Pij(0)=Pij(1)=…=Pij(k)=…Pij – вероятность перехода из состояния i в состояние j.

P – матрица переходных вероятностей.

P=(p_ij, i=0, n; j=0,n)

P= Pii – система остается в том же состоянии.

Pij_k - вероятность перехода из i в j за к-шагов.

Pk – вся матрица перехода за k-шагов.

4. Дискретные цепи Маркова: стационарное распределение вероятностей.

0 1 2 3 4 5

П₀ П_1…. П₅

Пi(k)=( П₀(k), П₁(k),…, П_n(k))^T - вектор распределения вероятностей состояния на к-том шаге.

х₀, х₁,…х_n

П(0) П(1)…П(k)

П(k+1)=P^T П(k)

Р – матрица переходных вероятностей за 1 шаг.

П(k)→ 1) существует предел П

k→∞ 2) не существует предел П

Дискретную цепь Маркова назовем эргодической, если существует предельное распределение вероятностей П=

П(k+1)= P^T П(k)

k→∞ k→∞

П= P^T П

П(0)=P П(1)=P^T П П(2)=П….

Если ДЦ является эргодической, то предельное распределение вероятности П является одновременно и стационарной. Если взять его в качестве начального, оно не будет изменяться.

Т: для неприводимой опериодической конечной цепи Маркова всегда существует предельное распределение вероятности - , независящая от начального распределения вероятности. При этом выполняются соотношения:

1) Пj= 1/Mj, о=0,n (все состояния цепи Маркова являются возвратными

2) П= P^T П ненулевыми) (*)

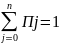
Соотношение (*) используется для нахождения стационарного распределения для ДЦМ.

4. Дискретные цепи Маркова: распределение времени пребывания в одном и том же состоянии.

Рассм. вероятность того, что на протяжении m шагов цепь М будет находиться в некот. i-ом состоянии, а на m+1 покинет это i-ое состояние% Дискретные цепи Маркова: распределение времени пребывания в одном и том же состоянии;

т	i	­ i
1	pii	1-p
2	Pii2	pii(1-pii)
3	Pii3	Pii2(1-pii)
….	…..	…..
m	piim	piim-1(1-pii)

P(X=m)=p^m+1(1-p)- геометр. распределение

Время пребывания дискретной цепи Маркова в одном и том же состоянии распределено по геометр. распределению.

Можно показать, что из cсвойства Маркова для дискрет. цепи вытекает геометрическое распределение времени пребывания в одном и том же состоянии и ,наоборот, если установлено, что для ДУ время пребывания в одном и том же состоянии распределено по геометр. закону, то эта цепь обладает свойством Маркова.

4. Непрерывные цепи Маркова: определение, уравнение Чепмена-Колмогорова. Непрерывной цепью Маркова будем называть случайный процесс (СП) с дискретным множеством состояний, непрерывно изменяющимся временем и обладающий свойством Маркова. Пусть t и t+Δt – два момента времени, Δt>0. Используя соотношение (3) можем записать .

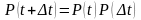Поэтому .

Рассмотрим предел: .

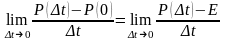Доказано, что при определенных условиях этот предел существует. Будем считать, что он существует и обозначим его .

(n×n)-матрицу Q называют матрицей интенсивностей однородной НЦМ.

В силу сделанного предположения существует предел

.

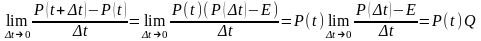Но

.

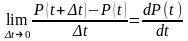Следовательно

. (2)

Дифференциальное матричное уравнение (2) называют уравнением Чепмена-Калмогорова для однородных НЦМ.

4. Непрерывные цепи Маркова: стационарное распределение вероятностей. Свяжем с каждым состоянием i цепи Маркова функцию π_i(t)=P(X(t)=i) – вероятность того, что в момент времени t система находиться в состоянии i. Из этих функций составим вектор распределения вероятностей состояний цепи Маркова в момент времени t:

.

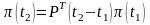Пусть t₁, t₂ – два момента времени, t₁<t₂. По аналогии с ДЦМ можно показать, что или , (3)

где верхний индекс T обозначает операцию транспонирования.

Из (3) следует, что если π(0) начальное распределение вероятностей состояний, то (4)

Продифференцируем равенство (4) и используем уравнение Чепмена –Колмогорова (2):

.

Таким образом получено дифференциальное уравнение, которому удовлетворяет распределение вероятностей состояний в произвольный момент времени: , (5)

которое вместе с начальным состоянием π(0) равенством используется для отыскания функций .

Однородную непрерывную цепь Маркова назовем эргодической, если существует ненулевой предел .

Вектор π будем называть предельным распределением вероятностей.

Очевидно, если взять предельное распределение вероятностей в качестве начального, то распределение вероятностей не будет изменяться во времени. Отсюда следует, что предельное распределение вероятностей π одновременно является стационарным распределением вероятностей состояний однородной НЦМ.