4. Отыскание экстремума функции n переменных. Градиент, линия уровня, их свойства.

f(x)-> min (1)

x€Rⁿ

x=(x₁,x₂,…,x_n)^T

1. – задача безусловной минимизации

Необходимое условие экстремума: 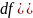, i=1,n (2)

Вектор, составленный из частных производных называется градиентом ф-ции в точке x.

(df(x)/dx1, df(x)/dx2, …, df(x)/dxn)^T=grad f(x)= f(x)

f(x*)=0 (3)

Соотношение (2) и (3) исп. для аналитического отыскания точек экстремума. Однако, решение системы уравнений (2) или (3) дело весьма сложное. Наряду с аналитическими существует большое число численных методов. Отметим гл. св-во grad: градиент представляет из себя вектор, задающий направление наискорейшего возрастания функции. Противоположный вектор называется антиградиентом и определяет направление наискорейшего убывания функции.

Линией уровня функции n-переменных будем называть мн-во точек x, на которых она принимает одно и тоже значение х: f(x)=const.

м/ду линией уровня и градиентом существует тесная связь: градиент всегда перпендикулярен к гиперплоскости, касательной поверхности.

На понятии градиента основано большое кол-во численных методов, кот. назыв. градиентными. Их суть можно сформулировать след. образом: выбираем начальную т. x₀ и из этой точки строим направление спуска (направление, в котором функция убывает).

Вектор l будем называть направлением спуска в точке х, если существует такое θ*>0, что f(x+ θl)<f(x) для любого θ из (0, θ*)

(x+ θl) – всегда задает линию в n-мерном пространстве.

4. Отыскание экстремума функции n переменных. Общая схема методов спуска.

Допустим, что известна некоторая начальная точка x⁰, построим х¹, х²…,х^k

x^k+1

1. Строим в т. x_k направление спуска l_k/

2. Решаем задачу одномерной минимизации:

min φ(θ)= f(х^k+ θl^k)

решение этой задачи обозначим через θ^k.

3. Переходим в новую точку по формуле: x^k+1=x^k+ θ^k l^k

4. Проверяем условие остановки: если оно выполнено, то x^k+1 принимаем в качестве приближенного значения х*, в противном случае переходим к п.1.

Условие остановки: 1)|f(x^k+1)- f (x^k)|<ε

2) |x^k+1 - x^k|<ε

4. Методы наискорейшего и покоординатного спуска для отыскания экстремума функции n переменных.

метод наискорейшего спуска.

l^k= - f(x^k)

метод покоординатного спуска.

Правило покоординатного спуска

Пусть i – номер координаты вектора х.

Рассм. i-ую компоненту градиента ф-ции f(x): _if(x)

В качестве направления l^k= -e_i sign _if(x^k)

4. Решение задач математического программирования путем сведения их к задачам безусловного экстремума. Метод штрафных функций.

F(х)->min (1)

Gi(х)<=0; i=1,n;

T(x,t)=f(х)+t*ϴ(х)

t-штраф ,коэф. Штрафа;

ϴ(x)- штрафная функция

ϴ(х) предъявляют след. требования:

ϴ(х)=0 для любой допустимой точки;

ϴ(х)>0 для любой допустим ой точки;

ϴ(х)не прерывная функция;

Рисунок

ϴ1(х)=∑[max{0,gi(x)}]²

ϴ2(x)=∑(gi(x)+│gi(x)│)²

На первой итерации задаем значение t¹ и решаем задачу: T(x,t¹)-> min;

Допустим, полученное решение обозначим через x^*1;

Увеличим штраф t²=r*t²; r=2,3…….(r>1)

Повторим решение:

T(x,t²)->min;

T^x

T(x,t^k)->min

X^*K

Проверяем условие останова: если ϴ(х)<Е-решение останавливаем. Иначе, увеличиваем штраф, переходим к след. итерации.

Т.О. получаем последовательность решений

Х^*1,х^*2,…..х^*t, …..

X^*k->x^*

Если │х^*к-х^*к+1│<Е можно исполь. в качестве критерия остановки решения