4. Численные методы одномерной минимизации: метод квадратичной интерполяции.

Если отрезок [a,b] небольшой, а функция f(x) достаточно гладкая (например, дважды дифференцируемая), то ее график близок к графику параболы (см. рис. 5). Если y=Ax²+Bx+C – уравнение параболы, то точка ее минимума находится без каких-либо проблем: 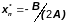. Поэтому очевидна идея: вместо исходной функции рассмотреть близкую к ней параболу, а точку её минимума принять в качестве приближенной точки минимума исходной функции. Известно, что для построения параболы нужно знать 3 точки, через которые она проходит. В качестве этих точек возьмем точки на графике функции f(x), соответствующие концам отрезка, и некоторой внутренней точке с (при отсутствии дополнительной информации в качестве этой точки можно взять середину отрезка: с=(a+b)/2).

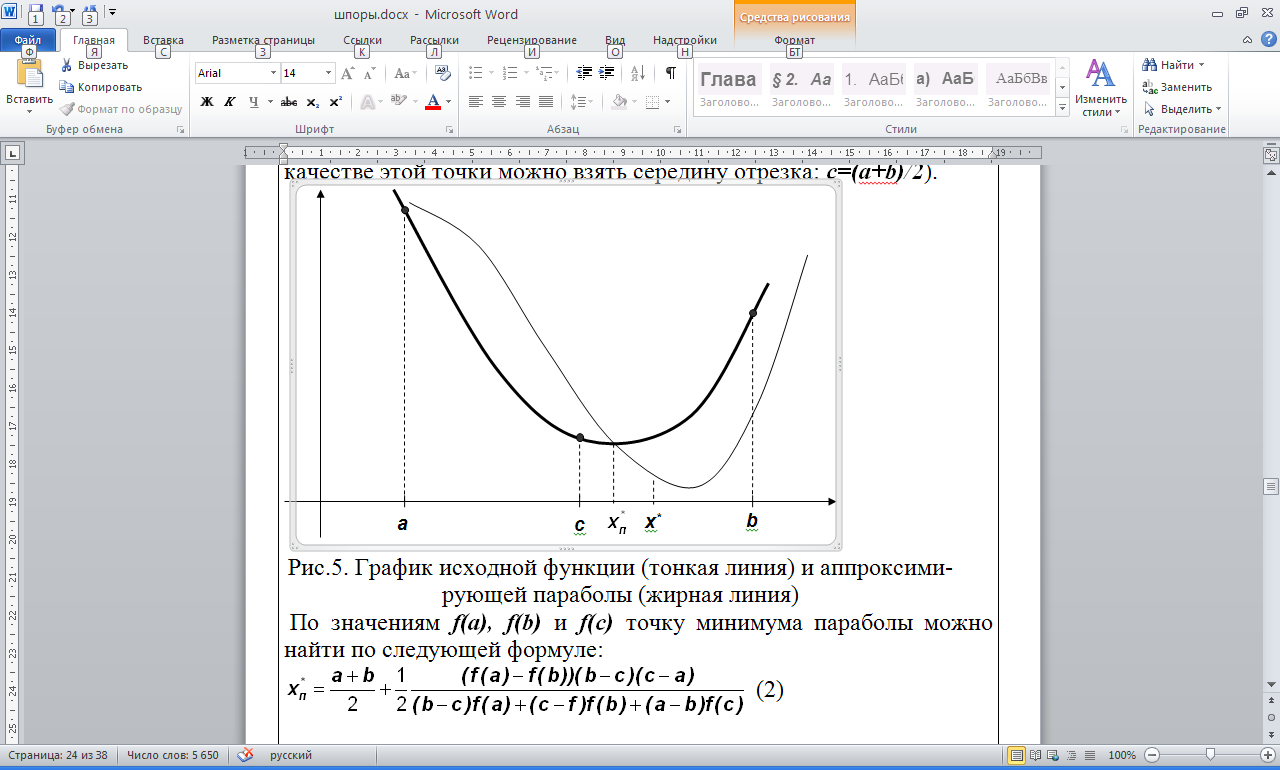Рис.5. График исходной функции (тонкая линия) и аппроксимирующей параболы (жирная линия)

По значениям f(a), f(b) и f(c) точку минимума параболы можно найти по следующей формуле:

(2)

Опишем теперь алгоритм метода сечения отрезка, базирующийся на идее метода квадратичной интерполяции. Допустим, что к началу k-ой итерации известны отрезок [a^k,b^k] и внутренняя точка c^k вместе с соответствующими значениями функции.

1) по формуле (2) найдем точку минимума параболы, которую для удобства обозначим δ^k. Для определенности предположим, что δ^k>c^k.

2) вычислим f(δ^k).

3) если f(δ^k)<f(c^k), то новый отрезок [a^k+1,b^k+1] построим так: a^k+1=c^k, b^k+1=b^k. В качестве точки c^k+1 примем точку δ^k.

В противном случае (f(δ^k)≥f(c^k)) положим: a^k+1=a^k, b^k+1=δ^k, c^k+1= c^k.

4) если , то перейдем к следующей итерации. В противном случае работа алгоритма завершена, .

4. Численные методы одномерной минимизации: методы первого и второго порядка.

В этом пункте будем предполагать, что функция f(x) непрерывна и дифференцируема нужное число раз, а точка минимума x* является внутренней точкой отрезка [a,b]. В этом случае она удовлетворяет необходимому условию экстремума:

. (3)

Поэтому вместо задачи отыскания минимума функции f(x) можно решать уравнение (3) и, следовательно, для отыскания экстремума можно использовать численные методы решения уравнений. Ниже рассматриваются два метода, базирующиеся на этом принципе.

Метод дихотомии (половинного деления). Пусть [a^k,b^k] – отрезок на k-ой итерации метода ([a¹,b¹]= [a,b]). Заметим, что на концах отрезка производная функции f(x) имеет значения различных знаков.

1) найдем середину отрезка c^k=(b^k-a^k)/2.

2) вычислим f'(c^k). Если f’(c^k)=0, то решение задачи окончено: x^*=c^k. В противном случае перейдем к п.3.

3) новый отрезок построим в зависимости от соотношения знаков значений производной функции в точке c^k и на одном их концов отрезка, например a^k. Если f’(c^k) и f’(a^k) имеют различные знаки, то a^k+1=a^k, b^k+1=c^k; в противном случае a^k+1=c^k, b^k+1=b^k.

4) если b^k+1-a^k+1<ε, то работа алгоритма завершена: . В противном случае переходим к следующей итерации.

В этом алгоритме используются производные 1-го порядка. Поэтому его можно отнести к методам 1-го прядка.

Метод Ньютона. Метод Ньютона базируется на популярном методе решения уравнений. Если g(x)=0 заданное уравнение, x0 – известное приближение к решению, то решение с заданной точностью находится по итерационной формуле:

(4)

Подставляя в формулу (4) вместо g(x) производную f’(x), получаем:

Этот метод откосится к методам второго порядка.