4. Математическое программирование: предмет исследования, общие сведения о численных методах отыскания экстремумов.

Задачи математического программирования – те задачи, в которых критерии качества и ограничения могут быть сформулированы аналитически.

f(x)→min (max) - критерий качества

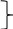gi(x)≤0, i=1,m - система

gi(0)=0, i=m+1,k ограничений

Необходимые и достаточные условие экстремума дают аналитические методы отыскания экстремума, т.е. методы, основанные на преобразовании уравнений, неравенств, в ходе которых находится точное решения или отсутствие такового у исследуемой задачи. На практике применение аналитических методов бывает трудно реализуемо либо вообще невозможно в силу сложности исходной функции, ее ограниченной дифференцируемости, сложности решения систем нелинейных уравнений. Поэтому наряду с аналитическими методами разработано большое количество численных методов, с помощью которых экстремум функции находится приблизительно, как предел сходимости последовательности точек. Численные методы разбиваются на классы в зависимости от порядка старшей производной, используемой при проведении расчетов. Методы нулевого порядка — это методы, которые не используют производных, т.е. в вычислениях используются только значения исходной функции. В методах первого порядка используются значения функции и ее первых производных и т.д.

4. Метод множителей Лагранжа.

Рассм. ЗМП

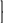f(x)->min (1)

gi(x)=0, i=1,m

составим спец. Функцию, кот. будем назыв. функцией Лагранжа

F(x,λ)=f(x)+λ₁g₁(x)+λ₂g₂(x)+…+λ_mg_m(x)

λ – вещественные переменные, которые назыв. множителями Лагранжа.

Имеет место след. теорема: если x^*=(x^*₁, x^*₂ ,…, x_n^*)^T- точка экстремума в задаче (1), то существует такой набор множителей λ ^*=( λ ^*₁, λ ^*₂ ,…, λ _n^*)^T, что выполняется условие Лагранжа

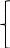
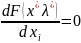, i=1, n

, i=1, m (2)

Условие (2) явл. необходимым, а не достаточным. Поэтому их можно уверенно исп. Только в тех точках, в кот. т. экстремума существует и единственна. В др. задачах т. x* удовл. (2) необходимо дополнительно проверять с/п. дост. усл.

4. Численные методы: общая характеристика методов отыскания экстремума функции одной переменной.

X⁰ – обычно задается

Для нахождения каждой след. т. решается вспомогательная более простая вспомогательная задача.

1. Должен существовать предел:

2. Предел должен совпадать с точкой экстремума x*: x= x*

Классификация численных методов осуществляется от того, какие производные исп. Для построения последовательности точек. Порядок старшей производной определяет порядок метода. В методах нулевого порядка исп. Только значение исходной ф-ции и ее производной. В методах 1-го порядка – значение ф-ции и ее производной. В методах 2-го порядка – значение ф-ции, ее производной, и 2 производной и т.д.

4. Численные методы одномерной минимизации: метод «золотого» сечения. Пусть [a^k,b^k] – отрезок на k-ой итерации метода ([a¹,b¹]= [a,b]). Точки , вычислим по правилу: ,

где l^k=b^k-a^k – длина отрезка, - коэффициент сечения,

.

Коэффициент сечения подобран специально. Точки сечения располагаются таким образом, что при переходе к новому отрезку [a^k+1,b^k+1] та из точек , , которая остается в новом отрезке, автоматически становится точкой разбиения нового отрезка (см. рис. 5).

Рис. 5. Примерная схема перехода точек сечения от отрезка к отрезку

Поэтому, если, например, , то новый отрезок [a^k+1,b^k+1] и его сечение строятся по правилам:

a^k+1=a^k, b^k+1= ;

, =

В силу этих правил нет необходимости вычислять значение функции в точке - оно было вычислено на предыдущей итерации. Его просто нужно запомнить и сохранить до нужного момента.

Собственно, в этом приеме суть метода «золотого» сечения, его «золото»: на каждой итерации метода (кроме первой) вычисляется только одно новое значение функции. При решении сложных задач, в которых одно вычисление функции занимает несколько минут, а то и часов, общее время вычислений может сократиться до двух раз.