35. Какой СП называется Марковским? Случайный процесс Маркова определяется следующим образом – это процесс, состояние которого в каждый следующий момент времени зависит только от состояния в текущий момент времени и не зависит от всех предыдущих состояний.

36. Какой сп называется полумарковским?

Полумарковские процессы – процессы, которые обладают свойством Маркова только в отдельно взятые моменты.

37. Какой сп называется процессом гибели и размножения?

процесс гибели и размножения - это случайный процесс, для которого

1. Вероятность рождения одного и только одного нового члена популяции на промежутке времени пропорциональна длительности этого промежутка и составляет , где - бесконечно малая величина от ;

2. Вероятность того, что на интервале не родится ни одного нового члена популяции составляет ;

3. Вероятность гибели ровно одного члена популяции на интервале пропорциональна длительности этого промежутка и составляет ;

4. Вероятность того, что на этом промежутке не произойдет ни одной гибели определяется соотношением

38. Дайте определение дискретной цепи Маркова (ДЦМ). Дискретной цепью Маркова будем называть последовательность случайных величин, принимающих значение из множества х= {0,1,2,…,n,…}, и обладающих cв-вом Маркова: Р(x_k+1=x_k+1| x_k=i_k, x_k-1=i_k-1,,…x₀=i₀)=P(x_k+1=i_k+1| x_k=i_k)

39. Что называется переходной вероятностью за 1 шаг? За k шагов?

Pij(k) – вероятность перехода за 1 шаг из состояния i в состояние j, если на k-ом шаге система находится в состоянии i.

Pij(0)=Pij(1)=…=Pij(k)=…=Pij – вероятность перехода из состояния i в состояние j.

Pijk – вероятность перехода из i в j за k шагов.

Pijk=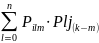

40. Какая ДЦМ называется однородной?

Однородная цепь Маркова – такая цепь, для которой переходная вероятность Pij зависит только от длины интервала [t1,t2] и не зависит от момент. t1, t2

41. Запишите уравнение Чепмена-Колмогорова для однородной ДЦМ (ОДЦМ).

Специальный случай уравнения Чепмена-Колмогорова:

P(X_n=i_n | X₀=i₀) = (Pⁿ)_i0,in

то есть матрица переходных вероятностей за n шагов однородной цепи Маркова есть n-я степень матрицы переходных вероятностей за 1 шаг.

P(X_n=i_n) = ((P^T)ⁿp)_in

42. Что такое «вектор распределения вероятностей состояний» для ОДЦМ?

π(k) = P(x(k)=i) – вероятность того, что на k-ом шаге ДЦМ находится в состоянии i

– вектор распределения вероятностей π(k) на k-ом шаге

43. Как связаны векторы распределение вероятностей состояние на k-ом и (k+1)-ом шагах.

π(k+1)=P^Tπ(k)

44. Что такое «предельное распределение вероятностей» ОДЦМ?

П

45. Что такое «стационарное распределение вероятностей» ОДЦМ? Если дискретная цепь явл. эргодической, то предельное распределение вероятности П явл. одновременно и стационарным.

46. Как найти стационарное распределение вероятностей точно?

Пj=1/Mj, j=0,n (все состояния ЦМ явл. возвратными ненулевыми)

П=P^T П(k)

47. Как найти стационарное распределение вероятностей приближенно?

48. П(k+1)=P^T П(k)

π(1)=P^Tπ(0)

…

π(k)=P^Tπ(k-1)≈ π (|π(k)- π(k-1)|≤ε)

49. По какому закону распределено время пребывания ОДЦМ в одном и том же состоянии. Запишите формулу, характеризующую данное распределение.

Время пребывания ДЦМ в одном и том же состоянии распределено по геометрическому распределению: P(X=m)=p^m-1(1-p)

50. Дайте определение непрерывной цепи Маркова (НЦП).

Непрерывной цепью Маркова будем называть случайный процесс (СП) с дискретным множеством состояний, непрерывно изменяющимся временем и обладающий свойством Маркова.

51. Что такое «переходная вероятность» на заданном промежутке времени (для НЦП)?

Пусть . Вероятность события при условии, что будем называть переходной вероятностью из состояния i в состояние j на промежутке времени [t,s] и обозначать ). или P_ij(t₁,t₂)=P(X(t₂)=j|X(t₁)=i) – переходная вероятность из состояния i в состояние j за время t₁, t₂.

52. Какая НЦМ называется однородной? Как определяется переходная вероятность для однородной НЦМ (ОНЦП)? Если переходная вероятность не зависит от расположения интервала [t₁,t₂] на временной оси, а только от его длины t=t₂-t₁ , то НЦМ называют однородной. Или: однородная цепь Маркова – такая цепь, для которой переходная вероятность P_ij зависит только от длины интервала [t₁,t₂] и не зависит от моментов t₁, t₂.

Pij(t1,t2)->Pij(t) – вероятность перехода из состояния i в j за время t.

53. Запишите уравнение Чепмена-Колмогорова для ОНЦМ.

54. Что такое «распределение вероятностей состояний» для ОНЦМ?

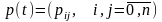
55. Запишите матричное дифференциальное уравнение, которому удовлетворяет распределение вероятностей состояний ОНЦМ.

56. Что такое «предельное распределение вероятностей» для ОНЦМ?

Однородную непрерывную цепь Маркова назовем эргодической, если существует ненулевой предел .

Вектор π будем называть предельным распределением вероятностей.

57. Что такое «стационарное распределение вероятностей» для ОНЦМ?

предельное распределение вероятностей π одновременно является стационарным распределением вероятностей состояний однородной НЦМ.

58. Как найти стационарное распределение вероятностей состояний для ОНЦМ?

59. Что такое «процесс гибели и размножения (ПГиР)»?

Процессом гибели и размножения называется непрерывная цепь Маркова, для которой переходы разрешены только в соседние.

60. Нарисуйте диаграмму переходов для ПГиР.

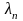
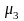
λ – интенсивность, с которой система переходит в состояние i

 – интенсивность, с которой система покидает состояние i

61. Что такое процесс «чистого» размножения? Нарисуйте диаграмму переходов процесса «чистого» размножения. Рассмотрим процесс гибели и размножения для которого интенсивность размножения постоянна (не зависит от состояния) и равна λ, т.е. λ₀= λ₁= …= λ_n-1= λ_n=…=λ. Интенсивность гибели в любом состоянии равна 0: μ₀= μ ₁= …= μ _n-1= μ _n=…=0. Такой процесс называется процессом чистого размножения. Процессу чистого размножения соответствует диаграмма

p₀(t) p₁(t) p₂(t) p₃(t) p_n(t) p_n+1(t)

62. Что такое процесс «чистой» гибели? Нарисуйте диаграмму переходов процесса «чистой» гибели. Рассмотрим процесс чистой гибели, который получается из обычного ПГР при следующих условиях:

λ₀= λ₁= …= λ_n-1= λ_n=…=0,

μ₀= μ ₁= …= μ _n-1= μ _n=…= μ.

Т.е. это процесс, у кот. интенсивности всех потоков размно-ния равны нулю.

62. Опишите связь между ПГиР и СМО. Можно сказать, что процесс гибели и размножения с постоянным интенсивностями размножения и гибели

λ₀= λ₁= …= λ_n-1= λ_n=…= λ,

μ₀= μ ₁= …= μ _n-1= μ _n=…= μ,

может быть интерпретирован как СМО, у которой

а) интервалы времени между поступающими заявками распределены по показательному закону A(t)=1- p₀(t)=1- e^-λt.;

б) интервалы времени обслуживания заявок распределены по показательному закону B(t)= 1- e^-μt;

в) отсутствуют отказы.

Из перечисленных свойств вытекает, что СМО в этом случае представляет элементарную систему массового обслуживания с одним обслуживающим прибором и без отказов (т.е. с накопителем бесконечной емкости), которая имеет обозначение M/M/1:

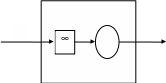
Верно и обратное: процесс поступления и обслуживания заявок в элементарной СМО типа M/M/1 представляет собой процесс гибели и размножения.