1. Какие модели относят к динамическому программированию? К динамическому программированию относятся задачи, которые по своей природе являются многошаговыми, либо задачи, кот. можно свести к многошаговыми: игровые, экономические, ряд задач техн. характера.

2. Сформулируйте принцип инвариантного погружения. Вместо конкретного n-шагового процесса рассматривается процесс с произвольным фиксированным количеством шагов 0≤k≤n

3. Сформулируйте принцип оптимальности: каждое следующее состояние динамической системы многошагового процесса однозначно определяется его текущим положением системы и целью управления.

4. Запишите математическую модель задачи о распределении ресурсов.

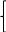
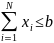
x_i≥0, i=1, N

5. В чем состоит принцип инвариантного погружения для задачи о распределении ресурсов?

1≤k≤N

0≤y≤b

y=0, Δb, 2 Δb,…, b

6. Что выражает функция Беллмана в задаче о распределении ресурсов? Функция Беллмана F_k(y) – выражает максимальную прибыль предприятия от распределения y единиц ресурсов между k-предприятиями.

7. Запишите рекуррентные соотношения Беллмана для задачи о распределении ресурсов.

F_k+1(y)=max (F_k(y-x_k+1)+f_k+1(x_k+1))

0≤x_k+1≤y (2)

F₁(y)=f₁(x₁)

8. Сформулируйте задачу о замене оборудования.

Предприятие на однотипном оборудовании производит некоторую продукцию. В зависимости от возраста оборудования меняется кол-во производимой продукции и затраты на обслуживание оборудования. Для характеристики работы оборудования исп. 2 величины: u(t) – сумма продукции (доход) V1 производимой в течении года, если возраст оборудования составляет z лет; v(t) – затраты на эксплуатацию и ремонт оборудования в течении года, если возраст оборудования в начале этого года составляет t лет. В начале каждого года рук-во предприятия принимает решение: производить ли продукцию в течении след. Года на старом оборудовании иди демонтировать это оборудование, продать по остаточной цене и заменить новым. При принятии этого решения учитывается, что на покупку нового оборудования необходимо p денежных единиц. Составить план оптимальной замены оборудования на промежутке T лет, если в начале этого промежутка возраст оборудования t₀ лет.

t₀ t₀₊₁ t₀₊₂

0 1 2 T

u(t)- r(t) – прибыль

9. Что выражает функция Беллмана в задаче о замене оборудования? Функция Беллмана F_k(t) выражает max прибыль предприятия на промежутке t лет, если возраст оборудования в начале этого промежутка t лет.

10. Запишите рекуррентные соотношения Беллмана для задачи о замене оборудования.

1. k=1

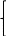
u(t)-r(t) (1)

S(t)-p+u(0)-r(0)

2. Рассм. k+1

u(t)-r(t)+ (2)

S(t)-p+u(0)-r(0)+

11. Запишите задачу математического программирования в общей форме. ЗМП будем называть задачу след. вида:

f(x)-> min

gi(x)=0, i=1,m

gi(x)≤0, i=m₁+1,m₂

12. Дайте определение унимодальной функции.

Рассмотрим задачу: 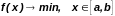. (1)

Функцию f(x) будем называть унимодальной на отрезке [a, b], если на этом отрезке существует такая точка минимума x^*, что для любых двух точек x₁, x₂ этого отрезка имеют место следующие соотношения:

x*≤х₁≤х₂→f(x*)≤f(x₁)≤f(x₂)

x*≥х₁≥х₂→f(x*)≤f(x₁)≤f(x₂)

13. Какая идея лежит в основе методов сечений для отыскания экстремума унимодальной функции?

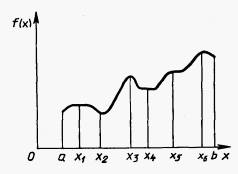
l=b-a; ε - погрешность

x₁=a+α*l

x₂=b-α*l

f(x₁)<f(x₂) -> внутри [a,x₁] существует точка минимума; [x₂,b] не содержит точки минимума, его можно отсечь

Когда (1- α)^kl<ε, метод прекращает работу

14. Что такое линия уровня функции n переменных? Линией уровня функции n-переменных будем называть множество точек х, на которых она принимает одно и тоже значение. х: f(x)=const

15. Что такое градиент функции n переменных? Вектор, составленный из частных производных, называется градиентом ф-ции в точке x.

(df(x)/dx1, df(x)/dx2, …, df(x)/dxn)^T=grad f(x)= f(x)

16. Как располагаются в пространстве градиент и касательная поверхность (плоскость, прямая) к линии уровня? Градиент всегда перпендикулярен к гиперплоскости, которая является касательной к линии уровня.

17. Что такое «направления спуска»? Вектор l будем называть направлением спуска в точке х, если существует такое θ*>0, что f(x+ θl)<f(x) для любого θ из (0, θ*)

(x+ θl) – всегда задает линию в n-мерном пространстве.

18. Нарисуйте геометрическую интерпретацию метода наискорейшего спуска.

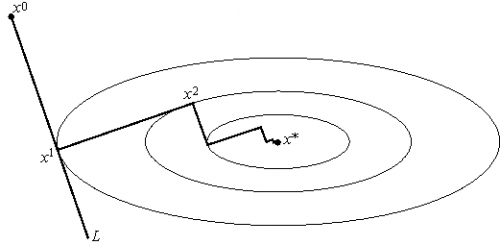
На каждом шаге λ^[k] выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L.

19. Нарисуйте геометрическую интерпретацию метода покоординатного спуска.

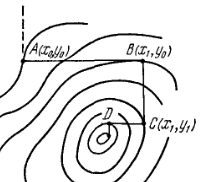
20. На какой идее основан метод штрафных функций?

Штрафовать за нарушение ограничений

21. На какой идее основан метод барьерных функций?

Штрафовать за приближение к границе.

22. Дайте определение системе массового обслуживания (СМО)? Почему конвейер не является СМО? СМО – техническая или соц. система, предназначенная для обслуживания поступающих в нее заявок. При этом интервалы времени между заявками, так и интервалы на их обслуживание носят случайный характер. В этом состоит отличие от конвейера, где это детерминированные величины.

23. Какая случайная величина используется для описания входного потока заявок?

λ – среднее кол-во заявок, поступающих в единицу времени в СМО или интенсивность входного потока.

24. Какая случайная величина используется для описания процесса обслуживания?

µ - интенсивность обслуживания, среднее кол-во заявок, кот. обслуживается прибором в единицу времени.

25. Какая СМО называется элементарной? Неэлементарной?

элементарной СМО называется СМО типа M/M/k

Элементарная – в которой входной поток и время обслуживания распределены по показательному закону. Неэлементарные – все остальные.

26. Какие основные факторы используются при классификации СМО?

A/B/m/k

A – закон распределения входного потока заявок

B – закон распределения интервалов времени обслуживания

m – количество обслуживающих приборов

k – количество мест для ожидания

27. Охарактеризуйте СМО типа M/M/1.

Элементарная система.

Входной поток распределён по показательному закону.

Время обслуживания распределено по показательному закону.

Количество обслуживающих приборов – 1.

Количество мест для ожидания - ∞.

28. Охарактеризуйте СМО типа M/M/∞.

Элементарная система без ожидания и отказов.

Входной поток распределён по показательному закону.

Время обслуживания распределено по показательному закону.

Количество обслуживающих приборов – ∞.

Количество мест для ожидания - ∞.

29. Охарактеризуйте СМО типа M/M/m.

Элементарная система.

Входной поток распределён по показательному закону.

Время обслуживания распределено по показательному закону.

Количество обслуживающих приборов – m.

Количество мест для ожидания - ∞.

30. Охарактеризуйте СМО типа M/M/m/k.

Элементарная система; накопитель ограничен.

Входной поток распределён по показательному закону.

Время обслуживания распределено по показательному закону.

Количество обслуживающих приборов – m.

Количество мест для ожидания - k.

31. Охарактеризуйте СМО типа G/Er/m/k.

Входной поток распределён по неизвестному закону.

Время обслуживания распределено по функции Эрлонга.

Количество обслуживающих приборов – m.

Количество мест для ожидания - k.

32. Что такое случайный процесс (СП)? Случайный процесс – это случайная величина, которая наблюдается и развивается во времени.

33. Какие факторы используются для классификации СП.

По временному параметру:

1. Время может изменяться непрерывно [0, ∞) – случайный процесс с непрерывным временным параметром.

2. Принимать определенные значения (t₁,t₂,…, t_k) – случайный процесс с дискретным временем.

По множеству состояний:

1. X(t) [0, ∞) – непрерывное

2. X(t) {0, 1, 2,…, n,…} - дискретное

34. Какой СП называется стационарным?

Случайный процесс X(t) называется стационарным, если все его вероятностные характеристики не меняются с течением времени t (так что, например, распределение вероятностей величины X (t) при всех t является одним и тем же, а совместное распределение вероятностей величин X (t₁) и X (t₂) зависит только от продолжительности промежутка времени t₂—t₁, т. е. распределения пар величин {X (t₁), X (t₂)} и {X (t₁ + s), X (t₂ + s)} одинаковы при любых t₁, t₂ и s и т.д.).