
- •8. Попросы самопроверки :
- •9. Литература
- •10. Информационно-дидактический блок (аннотация, пособия) Введение
- •Предмет информатика
- •Информация и ее свойства.
- •Информационные объекты и процессы.
- •Единицы измерения информации.
- •Хранение информации в эвм
- •Понятие о системах счисления
- •Десятичная система счисления
- •Двоичная система счисления
- •Арифметические действия над двоичными числами
- •Сложение
- •11. Самостоятельная работа.
- •11.2. Работа с преподавателем:
- •11.3. Контроль исходного уровня и заключительного уровня знаний:
Десятичная система счисления
Название "десятичная" объясняется тем, что в основе этой системы лежит основание десять. В этой системе для записи чисел используются десять цифр - 0,1, 2, 3, 4, 5, 6, 7, 8, 9 .
Десятичная система является позиционной, так как значение цифры в записи десятичного числа зависит от ее позиции или местоположения в числе.
Позицию, отводимую для цифры числа, называют разрядом.
Например, запись 425 означает, что число состоит из 4 сотен, 2 десятков и 5 единиц. Цифра 5 стоит в разряде единиц, цифра 2 - в разряде десятков, цифра 4 — в разряде сотен.
Если записать эти же цифры в другом порядке, например 524, то это число содержит 5 сотен, 2 десятка и 4 единицы.
При этом цифра 5 имеет наибольший вес и называется
старшей цифрой числа а цифра 4 - наименьший вес и называется младшей цифрой этого же числа. Различие весов цифр в числе 524 становится очевидным, если это число записать виде суммы:
5 * 102+2* 101 +4 * 10°
В этой записи число 10 - основание системы счисления. Для каждой цифр числа основание 10 возводится в степень, зависящую от позиции цифры, и умножается на эту цифру. Степень основания для единиц равна нулю, для десятков - единице, для сотен - двум и т. д.
Если десятичное число дробное, то оно тоже легко записывается в виде суммы, в которой степень основания для каждой цифры дробной части отрицательна и равна - 1 для старшей цифры дробной части - 2 для следующей цифры дробной части и т. л.
Например, десятичное число 384,9506 выразится суммой
384,9506=3 • 102 +8 * 101 +4 * 10°+9 * 10-1 +5 * 10-2+0 * 10-3+6 • 10-4;
856,25=8 * 102+5 • 101 - 6 * 10°+2 • 10-1-5 • 10~2;
12937,1=1 * 104+2 • 103+9 • 102+3 *10 +7 * 100 +1 * 10-1.
Таким образом, вес любой цифры десятичного числа представляет собой определенную целую степень десяти, а значение степени диктуется позицией соответствующей цифры.
Двоичная система счисления
В компьютерах применяется, как правило, не десятичная, а позиционная двоичная система счисления, т.е. система счисления с основанием 2.
В двоичной системе любое число записывается с помощью двух цифр 0 и 1 и называется двоичным
Для того чтобы отличить двоичное число от десятичного числа, содержащего только цифры 0 и 1, к записи двоичного числа в индексе добавляется признак двоичной системы счисления, например 110101,111,.
Каждый разряд (цифру) двоичного числа называют битом.
Как и десятичное число, любое двоичное число можно записать в виде суммы, явно отражающей различие весов цифр, входящих в двоичное число.
В этой сумме в качестве основания используется число 2. Например, для двоичного числа 1010101,101 сумма примет вид
1 - 26 +0 * 25 +1 * 24 +0 * 23+1*2 2 + 0 *21 +1* 2°+1 • 2-1 +0 • 2- 2 +1 * 2-3
Эта сумма записывается по тем же правилам, что и сумма для десятичного числа.
Выполняя в этой сумме арифметические операции по правилам десятичной системы, получим десятичное число 85,625. Таким образом, двоичное число 1010101,101 совпадает с десятичным числом 85,625, или 1010101Д012 =85,62510.
Правило перевода. Чтобы перевести число из двоичной системы в десятичную систему счисления, нужно двоичное число представить в виде суммы степеней двойки с коэффициентами - цифрами и найти эту сумму.
Существенным недостатком двоичной системы является то, что для записи числа в этой системе требуется довольно много цифр 0 и 1. Это затрудняет восприятие двоичных чисел человеком. Например, десятичное число 156 в двоичной системе имеет вид 10011100.
Рассмотрим перевод целого десятичного числа в двоичную систему счисления.
Пусть Ац = а n-1 х 2 n-1 +... + а 1 х 2 1 + а 0 х 2 0
- поделим Ац на 2, тогда неполное частное будет а n-1 х 2 n-1 + … +а1 ,а остаток а0
- полученное неполное частное опять разделим на 2, остаток от деления будет а1 и т.д.
- на n-м шаге получим набор остатков а 0, а 1, а 2, ..., а n-1, которые входят в двоичное представление числа Ац и совпадают с остатками от последовательного деления данного числа на 2. Но мы получим их в обратном порядке. Нужно только переписать их .
Ац = а n-1 а n-2 ... а 1 а 0
П ример
1. Перевести число 11 из десятичной
системы счисления в двоичную систему.
ример
1. Перевести число 11 из десятичной
системы счисления в двоичную систему.
Соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы и получим число в двоичной системе счисления:
Пример 2. Если десятичное число достаточно большое, то можно применить следующий вид записи:

соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы и получим число в двоичной системе счисления
36310 = 1011010112
Рассмотрим перевод правильной десятичной дроби в двоичную систему счисления.
Пусть Ац - правильная десятичная дробь ,тогда его можно записать в виде:
Адр = а -1 х 2 -1 + а -2 х 2 -2 +...
Если Адр умножить на 2 , то в правой части получим а -1 + а -2 х 2 -1 + а-3 х 2 -2 +...,
где а-1 - целая часть, она и даст нам старший коэффициент в разложении числа Адр по степеням 2. Оставшуюся дробную часть снова умножим на 2 и получим а -2 + а-3 х 2 -1 +... , где а-2 - второй коэффициент после запятой в двоичном представлении числа. Процесс продолжить до тех пор, пока в правой части не получим 0 или не будет достигнута требуемая точность вычислений.
Пример 3. Перевести число 0,75 из десятичной системы счисления в двоичную систему.
Проверка: 0,112 = 1 х 2 -1 + 1 х 2 -2 = 0,5 + 0,25 = 0,7510 |
Пример 4. Перевести число 0,7 из десятичной системы счисления в двоичную систему.
|
Этот процесс может продолжаться бесконечно, его обрывают на том шаге, когда считают, что получена требуемая точность.
А если число смешанное? Тогда нужно отдельно перевести целую часть и отдельно - дробную.
Пример 5. Перевести число 15, 2510
 Значит
15,2510 = 1111,012
Значит
15,2510 = 1111,012

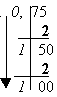 0,7510 = 0,112
0,7510 = 0,112