Решение типовых задач

Задача 13.1. Математическое ожидание количества выпадающих в течение года в данной местности осадков составляет 60 см. Определить вероятность того, что в этой местности осадков выпадет не менее 180 см.

Решение. Пусть СВ Х – количество осадков, выпадающих в течение года в данной местности. Так как Х>0 и известно только МО СВ Х, можно воспользоваться неравенством Маркова: Тогда

Задача 13.2. СВ Х имеет характеристики Оценить снизу вероятность события

Решение. Вместо неравенства X<2 будем рассматривать неравенство 0<X<2=|X–1|<1. Применяя неравенство Чебышева

получаем: Ответ: Р(А)0,96.

Задача 13.3. Вероятность появления события А в одном опыте постоянна и Р(А)= р =0,5. Сколько нужно провести независимых опытов, чтобы с вероятностью, не меньшей 0,975, гарантировать выполнение неравенства |w–p|<0,1, где w – относительная частота появления события А? Получить оценку для наименьшего числа опытов: а) используя неравенство Чебышева; б) считая применимой центральную предельную теорему.

Решение. а) Пусть n – необходимое число опытов, СВ Х – число появлений события А в n опытах. Тогда При этом По условию

б) Согласно центральной предельной теореме СВ , где – СКО индикатора события А, имеет при больших n нормальное распределение N(0, 1). Тогда

Отсюда По таблице функции (х)

ПЗ 14. Числовые и геометрические характеристики выборок. Точечные оценки параметров распределений.

Решение типовых задач.

Задача 14.1 Выборка представлена в виде дискретного статистического ряда. Найти:1) МО, дисперсию, СКО и моду; 2) построить эмпирическую функцию распределения; 3) предполагая, что выборка взята из ГС с биномиальным распределением признака, найти точечные оценки параметров биномиального закона.

хi	1	4	5	7
ni	10	20	14	6

Решение. 1) ;

;

2) Для построения эмпирической функции распределения найдем относительные частоты значений признака и накопленные относительные частоты:

хi	1	4	5	7
wi	0,2	0,4	0,28	0,12
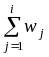
	0,2	0,6	0,88	1

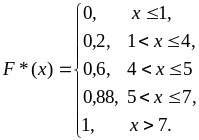
3) Биномиальное распределение имеет два параметра: n и p, где n – количество опытов, p – вероятность появления некоторого события в одном опыте. Для их оценки воспользуемся методом моментов, согласно которому сравниваются два теоретических момента с двумя соответствующими выборочными моментами. Сравним начальные моменты 1-го порядка и центральные моменты 2-го порядка. Для биномиального распределения Соответствующие выборочные моменты найдены выше: Получаем:

Задача 14.2 Из ГС, признак Х которой распределен нормально, произведена выборка объема n = 50. Выборочные данные:

19.1	17.4	14.8	19.7	18.7	14.9	17.8	14.9	17.1	15.8
17.1	17.9	16.2	15.9	15.8	16.5	16.3	17.7	15.6	17.3
13.1	17.2	15.6	20.9	19.8	18.5	16.3	15.3	15.9	16.9
17.2	19.7	18.4	16.8	16.4	19.8	20.5	17.5	17.9	17.1
18.2	17.4	14.9	16.8	16.5	15.2	17.1	15.7	18.4	15.9

Требуется: 1) составить интервальный статистический ряд; 2) найти выборочные характеристики (среднее значение, моду, медиану, дисперсию и СКО); 3) построить гистограмму; 4) найти точечные оценки параметров нормального распределения.

Решение. 1) Для составления интервального статистического ряда упорядочим значения признака Х в возрастающем порядке:

13.1	14.8	14.9	14.9	14.9	15.2	15.3	15.6	15.6	15.7
5.8	5.8	15.9	15.9	15.9	16.2	16.3	16.3	16.4	16.5
16.5	6.8	16.8	16.9	17.1	17.1	17.1	17.1	17.2	17.2
17.3	7.4	17.4	17.5	17.7	17.8	17.9	17.9	18.2	18.4
18.4	18.5	18.7	19.1	19.7	19.7	19.8	19.8	20.5	20.9

Как видно Хmin =13,1, Xmax =20,9. Количество интервалов выбираем по формуле: Длины интервалов находим по формуле Далее определяем границы интервалов и их середины Подсчитываем количество значений n_i признака, попавших в каждый интервал (в предыдущей таблице жирным шрифтом отмечены конечные значения признака для каждого интервала). Полученные данные заносим в расчетную таблицу (первые четыре столбца).

Расчетная таблица

i	(ai–1, ai)	xi	ni	xini	xi2ni
1	(13.1, 14.4)	13.75	1	13.75	189.06
2	(14.4, 15.7)	15.05	8	120.4	1812.02
3	(15.7, 17.0)	16.35	15	245.2	4009.84
4	(17.0, 18.3)	17.65	15	264.8	4672.84
5	(18.3, 19.6)	18.95	5	94.75	1795.51
6	(19.6, 20.9)	20.25	6	121.5	2460.37
Суммы			50	860.4	14939.65

Эти первые 4 столбца и определяют интервальный статистический ряд.

2) В 5-м и 6-м столбцах расчетной таблицы подсчитываем x_in_i и x_i²n_i. По суммам этих столбцов определяем начальные моменты 1-го и 2-го порядков:

.

Далее выписываем значения числовых характеристик

Моду находим по формуле где j – номер модального интервала (с наибольшей частотой), a_j–1 – начало модального интервала, h – его длина. В качестве модального интервала можно взять 3-й или 4-й. Выберем 4-й. Так как n₃=n₄, то

Медиану находим по формуле 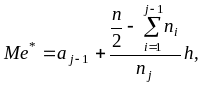где j – номер медианного интервала. Так как , а то 4-й интервал является медианным. Тогда

3)

P_i

14,4

13,1

15,7

19,6

20,9

X

17

18,3

Вид гистограммы.

4) Так как параметрами a и  нормального распределения являются МО и СКО, то по методу моментов оценками параметров являются

ПЗ 15. Интервальные оценки параметров распределений. Статистические гипотезы и их опытная проверка.

Решение типовых задач.

Задача 15.1. Из нормально распределенной ГС с неизвестными параметрами m и  произведена выборка объемом n=50. Выборочные данные: 1) Найти доверительные интервалы для параметров m и  при доверительной вероятности =0,95 (=0,05). 2) Проверить, согласуются ли выборочные данные с гипотезами: а) Н₀: m=10; б) Н₀: ²=9 при альтернативных гипотезах в п. а) Н₁: m10, в п. б) Н₁ ²9 и при уровне значимости =0,05.

Решение. 1) Доверительные интервалы для параметров m и ² нормального распределения имеют вид

Вычисления:

2а) Гипотеза H₀: (H₁: ) проверяется по выборке объема n при помощи статистики Эта статистика имеет распределение Стьюдента с n–1 степенями свободы. Правило проверки: H₀ отвергается на уровне значимости  если В данном случае По таблице двусторонних квантилей распределения Стьюдента Так как 1,074 < 2,008, то гипотеза Н₀ не противоречит выборочным данным.

2б) Гипотеза H₀: (H₁: ) проверяется при помощи статистики 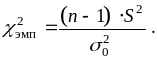H₀ отвергается на уровне значимости , если или . По таблице квантилей распределения хи-квадрат По выборочным данным Так как 31,61<61,31<70,11, то гипотеза Н₀ не противоречит выборочным данным.

Отметим, что гипотезы в п. а) и б) являются параметрическими и область принятия гипотез совпадает с доверительными интервалами для параметров. Это означает, что гипотезы не отвергаются, если числа m и  принадлежат соответственно интервалам (6,31; 12,678) и (2,799; 4,169).

Задача 15.2. На двух станках А и В производят одну и ту же продукцию, контролируемую по внутреннему диаметру изделия. Из продукции станка А была выборка из n=16 изделий, из продукции станка В – m=25 изделий. Выборочные оценки контролируемых размеров

Используя двусторонний двухвыборочный критерий, проверить гипотезу о равенстве математических ожиданий контролируемых размеров в продукции обоих станков при уровне значимости =0,05 и в предположении, что выборки произведены из двух нормально распределенных ГС.

Решение. Предварительно проверим гипотезу о равенстве дисперсий с помощью статистики 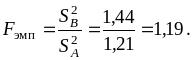По таблице квантилей распределения Фишера Так как 1,19<2,29, то можно считать, что .

Тогда статистика для проверки гипотезы H₀: о равенстве математических ожиданий имеет вид

При справедливости гипотезы H₀ эта статистика имеет распределение Стьюдента с n+m–2 степенями свободы. Правило применения (двустороннего) критерия заключается в следующем: гипотеза H₀ отвергается на уровне значимости , если Значение статистики

Так как то гипотеза Н₀ принимается.

Задача 15.3. Испытывались 4 партии радиоэлектронной аппаратуры. Получены следующие данные:

Номер партии	1	2	3	4
Число отказов	4	1	0	2

Предполагая, что число отказов распределено по закону Пуассона, найти 95%-й доверительный интервал для среднего числа отказов.

Решение. В данном случае число опытов n=4. Сумма принятых значений х=4+1+0+2=7, 2х=14, 2х+2=16,  = 0,05, /2 = 0,025, 1– /2 = 0,975, n=4. По таблице квантилей распределения хи-квадрат

ПЗ 16. Построение законов распределения признаков в ГС.

Решение типовых задач.

Задача 16.1. Задан дискретный статистический ряд (задача 14.1)

хi	1	4	5	7
ni	10	20	14	6

Согласуются ли эти данные с предположением о том, что признак Х распределен по биномиальному закону при уровне значимости 0,05?

Решение. При решении задачи 14.1 найдены числовые характеристики данного ряда и оценены параметры предполагаемого биномиального распределения: . Для подсчета теоретических частот множество значений признака Х разбиваем на интервалы специальным образом (чтобы принятые значения попадали только в один из интервалов), подсчитываем на ЭВМ теоретические вероятности и теоретические частоты попадания в интервалы. Получаем таблицу

хi	[0; 2,5)	[2,5; 4,5)	[4,5; 6,5)	[6,5; 19]
ni	10	20	14	6
ni/	9.1	20.7	15.2	5.0

Вычисляем статистику критерия хи-квадрат:

.

По таблице квантилей распределения хи-квадрат находим

Так как то гипотеза о том, что признак Х распределен по биномиальному закону принимается.

Замечание. При разбиении на интервалы каким-либо другим способом гипотеза о биномиальном распределении могла быть отклонена.

Задача 16.2. Задан интервальный статистический ряд (задача 14.2)

i	(ai–1, ai)	xi	ni
1	(13.1, 14.4)	13.75	1
2	(14.4, 15.7)	15.05	8
3	(15.7, 17.0)	16.35	15
4	(17.0, 18.3)	17.65	15
5	(18.3, 19.6)	18.95	5
6	(19.6, 20.9)	20.25	6

Проверить гипотезу о том, что признак Х распределен по нормальному закону при уровне значимости 0,05.

Решение. При решении задачи 14.2 найдены числовые характеристики данного ряда и оценены параметры предполагаемого нормального распределения: В качестве несмещенной оценки  возьмем исправленное СКО Для проверки гипотезы составляем расчетную таблицу: 1-й столбец – нормированные границы интервалов ; 2-й – значения функции Лапласа Ф(b_i); 3-й–теоретические вероятности p_i= Ф(b_i)– Ф(b_i-1); 4-й–теоретические частоты n_i^/ = 50p_i. Так как на 1-м и 6-м интервалах теоретические частоты меньше 5-ти, эти интервалы объединяем с соседними. В 5-й столбец помещаем теоретические частоты после объединения интервалов. В 6-й столбец помещаем эмпирические частоты после объединения интервалов. Получаем следующую таблицу

bi	Ф(bi)	pi	ni/	Объединенные	ni
-	-0.5			теорет. частоты
-1.699	-0.455	0.045	2.233
-0.912	-0.319	0.136	6.807	9.040	9
-0.126	-0.05	0.269	13.453	13.453	15
0.661	0.246	0.296	14.791	14.791	15
1.447	0.426	0.18	9.018	12.715	11
+	0.5	0.074	3.697

Вычисляем статистику критерия хи-квадрат:

.

По таблице квантилей распределения хи-квадрат находим

Так как то гипотеза о том, что признак Х распределен по нормальному закону принимается.

ПЗ 17. Регрессионно–корреляционный анализ.