Решение типовых задач

Задача 11.1. Точка (X, Y), изображающая объект на круглом экране радиолокатора, распределена с постоянной плотностью C в пределах круга K радиуса r с центром в начале координат (см. рисунок). Найти: 1) C; 2) плотности вероятностей компонент X и Y; 3) условные плотности вероятностей и ; 4) установить зависимость (независимость) СВ X и Y; 5) найти числовые характеристики ; 6) построить функции регрессии X на Y и Y на X.

Y

r

K

x

Х

0

Рисунок к задаче 11.1.

Решение. 1) По условию

2) Плотность вероятности компоненты Х находим по формуле

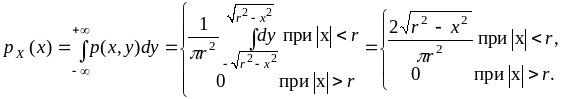
Аналогично,

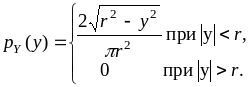
3) Условные плотности распределений найдем по формуле (8.5):

Как видно, условная плотность при каждом конкретном значении является равномерным распределением в промежутке Аналогичное утверждение имеет место и для условной плотности .

4) Так как то СВ X и Y зависимы.

5) аналогично

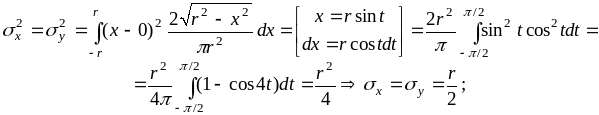
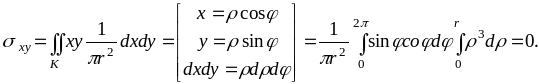
6)

Задача 11.2. Плотность вероятности двумерной СВ (X,Y) имеет вид

Требуется: 1) составить ковариационную и корреляционную матрицы; 2) найти уравнения функций регрессии X на Y и Y на X.

Решение. 1) На рисунке изображена область G, определяемая системой неравенств .

Y

1

G

x = y

0

X

Вычисление двойного интеграла по G можно провести двумя способами:

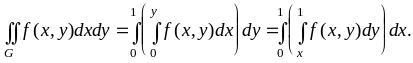
Вычисляем начальные моменты 1-го и 2-го порядков:

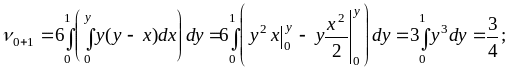
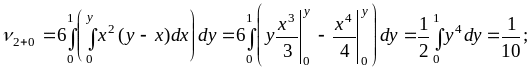
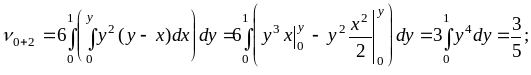
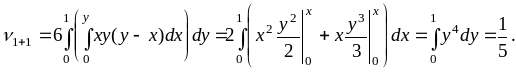
Тогда

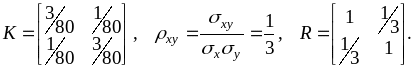
2) Плотности вероятности компонент Х и Y:

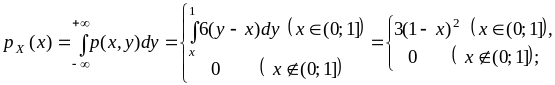
Условная плотность компоненты Х и функция регрессии Х на Y:

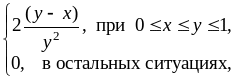
Аналогично



Задача 11.3. Двумерное нормальное распределение системы (X, Y) задано математическими ожиданиями и ковариационной матрицей:

Выписать и выражения функций регрессий X на Y и Y на X.

Решение. По определению, ковариационная матрица

.

Отсюда Тогда Для двумерного нормального распределения обе функции регрессии линейные, т. е. Подставляя численные, получим



ПЗ 12. Функции от СВ. Свойства числовых характеристик.

а). Предположим, что для дискретной СВ Х _X = {x₁, x₂, ..., x_n }, P(X=x_i) = p_i. Пусть (х)  некоторая функция действительного переменного х, определенная для всех значений СВ Х. По определению СВ Y=(X) задается следующей таблицей:

Y	(x1)	(x2)	...	(xn)
P	p1	p2	...	pn

Для получения ряда распределения СВ Y=(X), нужно значения в первой строке таблицы упорядочить по возрастанию. Если есть одинаковые значения, то их записывают как одно значение, а соответствующие вероятности складывают. Числовые характеристики СВ Y= (X) можно вычислять без построения ряда распределения. Приведем формулы для начальных моментов, через которые выражаются другие характеристики:

.

Задача 12.1. Число X неисправностей на участке высоковольтной линии в течение года имеет распределение Пуассона с параметром a. Общий материальный ущерб от этих неисправностей пропорционален квадрату их числа: Y=CX² , где С – неслучайная величина. Найти закон распределения ущерба и его математическое ожидание (средний ущерб).

Решение. Так как при km (k0, m0) k²m², то множеством значений СВ Y ,будут квадраты целых неотрицательных чисел, помноженные на С, т. е. _Y={С0, С1², С2², ..., Сk²,...}, которые принимаются с вероятностями т. е. ряд распределения СВ Y известен. Для распределения Пуассона

M(X) = ₁ = a, D(X)= ₂–(₁)²=a  ₂=(₁)²+a=a²+a.

Тогда



б). Пусть X  непрерывная СВ, F(x) и p(x) ее функция распределения и плотность вероятности, а y=(x) – некоторая функция, определенная для всех x_X. Введем понятие СВ Y, как функции от СВ X: Y= (X). По определению _Y={(x), x_X}. Если функция  имеет обратную, т. е. она монотонна на множестве _X и уравнение y=(x) однозначно разрешимо относительно x: x=g(y), то

Если же функция y=(x) не является монотонной, то решение неравенства (X)<y будет состоять из объединения непересекающихся интервалов, которые определяются в каждом конкретном случае. При этом выражение превратится в сумму вероятностей попадания СВ Х в указанные интервалы.

Основные числовые характеристики СВ Y= (X) можно найти без построения ее закона распределения:

.

Задача 12.2. Задана функция распределения СВ Х:

Найти закон распределения СВ и МО m_y.

Решение. Предварительно найдем m_y без построения закона распределения. Плотность вероятности СВ Х отлична от нуля при x>1 и равна p_X(x)=6x^–7. Тогда

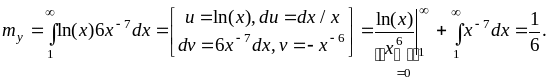
Так как функция монотонно возрастает при x>1 и существует обратная функция то

Дополняя получаем, что закон распределения СВ Y является показательным с параметром =6. Отметим, что для показательного распределения 

в) Пусть (X,Y) двумерная дискретная СВ, _={x₁, x₂,..., x_m}, _ = {y₁, y₂,..., y_n} P(X=x_i, Y=y_j) = p_i,j и z=(x,y) числовая функция двух переменных, определенная для всех x_X, y_. По определению СВ Z=(X,Y) является одномерной дискретной СВ с множеством значений _Z={(x_i,y_j), i=1,2,...,m; j = 1,2,...,n} и вероятностями P(Z=(x_i, y_j))= p_i,j. Основные числовые характеристики функции Z=(X,Y):

Если СВ X и Y независимы, то p_i,j = P(X=x_i)Р(Y=y_j).

Задача 12.3. Независимые СВ X и Y заданы рядами распределения

X	–1	0	1		Y	0	2	4
P	0,3	0,2	0,5	,	P	0,2	0,4	0,4	.

Составить ряд распределения СВ Z=XY.

Решение. Выпишем «неупорядоченный» ряд распределения СВ Z:

Z	–10	–12	–14	00	02	04	10	12	14
P	0,30,2	0,30,4	0,30,4	0,20,2	0,20,4	0,20,4	0,50,2	0,50,4	0,50,4	,

После вычислений расположим значения первой строки в порядке возрастания и объединим одинаковые значения (значение 0 повторилось 5 раз). В результате получим следующий ряд распределения СВ Z:

Z	–4	–2	0	2	4
P	0,12	0,12	0,36	0,2	0,2	, 

г) Рассмотрим двумерную непрерывную СВ (X,Y) с функцией распределения F(x,y) и плотностью вероятности p(x,y). В общем случае, когда Z=(X,Y) функцию распределения СВ Z можно найти в виде

F_Z(z)=P(Z<z)= ,

где область G(z)R² определяется неравенством (x,y)<z.

Если Z=aX+bY+c, где a b и c – неслучайные числа, причем a0 и b0, то для F_Z(z) и p_Z(z) получим выражения:

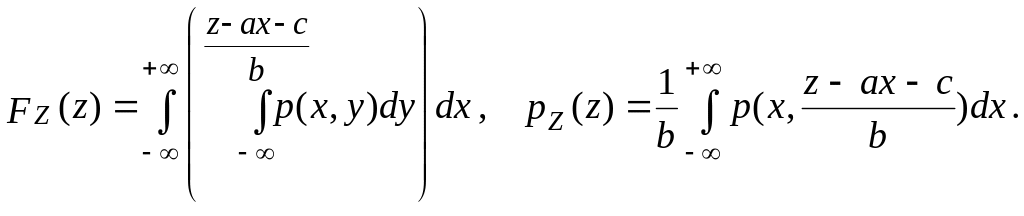
При Z=XY

При

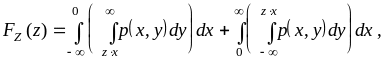
Задача 12.4. Две независимые СВ X и Y распределены по показательным законам с параметрами ₁ и ₂ соответственно. Найти: 1) плотности вероятности суммы U=X+Y и разности V=X–Y; 2) дисперсию произведения Z=XY.

y

y

u

G(u)

G(v)

x=y+v

y=u–x

x

u

x

v

0

0

Решение. 1) Так как X0 и Y0, то и U0. СВ V может принимать значения разных знаков. Функции распределений СВ U и V имеют вид

где области G(u) и G(v) определяются неравенствами x+y<u и x–y<v соответственно. Эти области изображены на рисунках.

Пределы интегрирования по области G(u): По области G(v):

Тогда для функции распределения СВ U получим выражение

Дифференцируя это выражение по u найдем плотность вероятности СВ U:

Аналогично, . После вычисления интегралов Отметим, что при v0 t=0, а при v<0 t= –v. Находя производную от , получим выражение плотности вероятности :

2). Для показательного распределения с параметром  начальные моменты Так как X и Y независимы, то для Z=XY.

ПЗ 13. Закон больших чисел и предельные теоремы теории вероятностей.

а). Контрольная работа по теме «Двумерные СВ» (1 час).

б). Неравенства Маркова и Чебышева. Теоремы Чебышева и Ляпунова.