Решение типовых задач.

Задача 8.1. Задана функция распределения непрерывной СВ Х:

Найти: 1) коэффициенты a и b; 2) плотность вероятности СВ Х; 3) m_x, D_x, _x, As, _x; 4) Mo, Me.

Решение. 1) Коэффициенты a и b определяем из условия непрерывности функции F(x). Возможные точки разрыва –1 и 1. Находим пределы F(x) слева и справа от этих точек:

Сравнивая, получаем систему

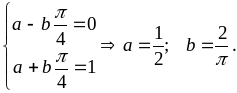
2) Вычисляя производную от F(x), получаем

.

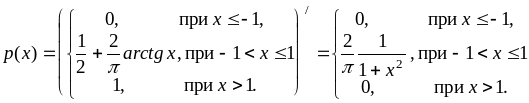3) Так как p(x) отлична от нуля только в промежутке (–1; 1), то при нахождении числовых характеристик несобственные интегралы в пределах от – до + следует заменить интегралами в пределах от –1 до 1. Так как интегралы от нечетных функций по симметричному промежутку равны нулю, то Дисперсия

.

Центральный момент 4-го порядка

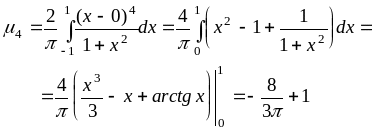
Тогда

4) Легко заметить, что функция принимает наибольшее значение при х=0, т. е. Mo=0. Из уравнения для медианы следует, что 

Задача 8.2. Непрерывная СВ Х имеет плотность вероятности

.

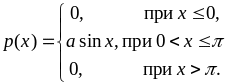Требуется: 1) найти коэффициент a; 2) построить функцию распределения; 3) определить вероятность того, что в результате опыта СВ Х примет значение из интервала (0; /3).

Решение. 1) Коэффициент a можно найти из условия нормировки

.

2) Функцию распределения находим по формуле При Если .

3) 

ПЗ 9. Примеры законов распределения.

Важнейшие примеры СВ дискретного и непрерывного типа рассмотрены в лекции 6. Приведем для каждой из них определение, закон распределения (ряд распределения или плотность вероятности) и числовые характеристики.

а). Биномиальное распределение. Пусть вероятность наступления некоторого события А в каждом из n независимых опытов постоянна и равна p (0<p<1), q=1–p — вероятность не появления события А. Введем СВ Х — число наступлений события А в n независимых опытах. Множество значений СВ Х и вероятности, с которыми они принимаются:

_X={0, 1, 2, ..., k, ...,n}; .

Основные числовые характеристики:

Мода: если np–q является целым числом, биномиальное распределение имеет две моды np–q и np+p. В противном случае модой является целое число, заключенное между np–q и np+p.

б). Распределение Пуассона:

_X={0, 1, 2, ..., k, ... };

в). Геометрическое распределение. Пусть вероятность появления события A в одном опыте равна p, р(0; 1), q=1–p. Опыты проводятся до первого появления события A. СВ X  число проведенных опытов. Тогда

_X ={1, 2, ..., k, ...}, P(X=k)=q^k–1p,

г). Равномерное распределение. Будем говорить, что СВ Х имеет равномерное распределение на отрезке [a, b] (подчиняется закону R[a, b]), если ее плотность вероятности определяется формулой

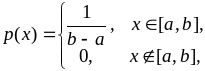
т. е. равна константе на [a, b] и нулю вне [a, b]. Числовые характеристики:

Если то .

д). Показательное (экспоненциальное) распределение. С простейшим потоком событий связана СВ T  время, прошедшее между появлением двух последовательных событий простейшего потока. Функция распределения и плотность вероятности СВ T:

.

В общем случае СВ Т называют показательным (экспоненциальным) распределением. Основные формулы:

Если для показательного распределения известно среднее время Т_ср, то параметр .

е). Нормальное распределение. СВ X называется нормальным распределением с параметрами a и , если множество ее значений совпадает с множеством действительных чисел, а плотность вероятности определяется формулой

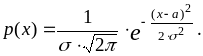
Обычно пишут X=N(a,). Числовые характеристики:

Функция распределения нормального закона:

, где .

Значения функции Ф(х) можно найти по таблице. При этом вероятность попадания нормально распределенной СВ X в интервал (, )

.

При  получаем е правило трех сигм:

т. е. значения нормально распределенной СВ практически не выходят за пределы интервала ( а –, а +).

Решение типовых задач рассмотрены в лекции 6 (примеры 6.1 – 6.5).

ПЗ 10. Дискретные двумерные СВ.

а). Контрольная проверочная работа по теме «Одномерные СВ» (1 час). Типовой вариант.

Задание 1 (дискретные одномерные СВ). Вероятность сдачи данного экзамена для каждого из 5-ти студентов равна 0,8. СВ Х – число студентов, сдавших экзамен. Записать закон распределения СВ Х. Найти числовые характеристики m_x, D_x, _x, Mo. Построить функцию распределения и ее график.

Задание 2 (непрерывные одномерные СВ). Задана плотность вероятности (или функция распределения) непрерывной СВ Х:

Найти коэффициент ‘a’ и числовые характеристики m_x, D_x, _x, Me , As, _х.

Задание 3 (частные законы распределения). СВ Х распределена нормально с математическим ожиданием, равным 40 и дисперсией, равной 100. Найти P(30<X<80).

б) Дискретные двумерные СВ (1 час). Дискретные двумерные СВ задаются матрицей вероятностей (лекция 7, п. 7.1). Методы решения основных задач рассмотрим на примерах.

Задача 10.1. Двумерная дискретная СВ (X,Y) задана матрицей распределения вероятностей в виде следующей таблицы:

Y X	1	2	3	4
0	0,06	0,1	0,12	0,08	0,36
5	0,11	0,09	0,07	0,13	0,4
10	0,05	0,08	0,05	0,06	0,24
	0,22	0,27	0,24	0,27

Требуется: 1) найти законы распределения компонент X и Y; 2) определить, зависимы или независимы компоненты X и Y; 3) найти условный закон распределения компоненты Y при условии, что компонента Х приняла значение Х=5; 4) найти m_x, D_x, _x, m_y, D_y, _y ; 5) построить ковариационную и корреляционную матрицы.

Решение. 1) В заданной таблице: 1-й столбец – множество значений СВ Х; 1-я строка – множество значений СВ Y; на пересечениях строк и столбцов стоят вероятности . Суммы вероятностей по строкам записываем в дополнительный (последний) столбец, а суммы вероятностей по столбцам – в дополнительную (последнюю) строку таблицы. Тогда 1-й и последний столбцы определяют закон распределения компоненты Х, а 1-я и последняя строки – компоненты Y, т. е. ряды распределения компонент определяются таблицами

X	0	5	10		Y	1	2	3	4
P	0,36	0,4	0,24		P	0,22	0,27	0,24	0,27

2) Компоненты X и Y называются независимыми, если для всех пар значений Если же хотя бы для одной пары это соотношение не выполнено то X и Y зависимы. Проверка: Р(X=0, Y=1) = 0,06; Р(X=0)Р(Y=1) = 0,360,22 = 0,0792  0,06  компоненты X и Y зависимы.

3) Для построения условного распределения СВ при условии, что СВ Х приняла значение 5, следует разделить вероятности в строке Х=5 на их сумму. В результате получаем условный закон распределения СВ Y/5

Y / 5	1	2	3	4		Y /5	1	2	3	4
P					или	P	0,275	0,225	0,175	0,325

4) Числовые характеристики компонент

5) Для построения ковариационной матрицы найдем корреляционный момент (ковариацию) по формуле Вычисления:

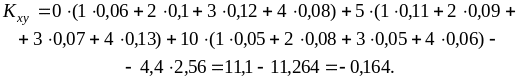
Коэффициент корреляции Тогда ковариационная и корреляционная матрицы запишутся в виде

.

Задача 10.2. Заданы ряды распределения независимых СВ X и Y:

X	2	4	6		Y	3	5	7
P	0,3	0,5	0,2		P	0,2	0,7	0,1

Построить матрицу вероятностей системы (X, Y).

Решение. Для независимых СВ P(X=x_i, Y=y_j)= P(X=x_i) P(Y=y_j). Тогда искомая матрица принимает вид

Y X	3	5	7
2	0,06	0,21	0,03
4	0,10	0,35	0,05
6	0,04	0,14	0,02	

ПЗ 11. Двумерные непрерывные СВ.