Решение типовых задач.

Задача 4.1. Некоторая продукция изготавливается на 3-х заводах. 1-ый завод изготавливает 30% продукции, 2-ой – 45%, 3-ий – 25%. Известно, что 1-й завод выпускает 80% продукции высшего качества, 2-й – 70%, 3-й – 75%. Найти вероятность того, что: а) взятая наудачу из общей массы единица продукции окажется высшего качества; б) единица продукции, оказавшаяся высшего качества, изготовлена на заводе №1.

Решение. а) Пусть событие A – «взятая наудачу продукция высшего качества», H₁ – «наудачу взятая продукция изготовлена на заводе №1», H₂ – «наудачу взятая продукция изготовлена на заводе №2», H₃ – «наудачу взятая продукция изготовлена на заводе №3». Вычислим вероятности гипотез и условные вероятности:

P(H₁) = 30/100 = 0,3, P(H₂) = 45/100 = 0,45, P(H₃) = 25/100 = 0,25,

P(A/H₁) = 80/100 = 0,80, P(A/H₂) = 70/100 = 0,70, P(A/H₃) = 75/100 = 0,75.

По формуле полной вероятности:

P(A) = 0,3·0,8+0,45·0,7+0,25·0,75 = 0,7425.

б) Т.к. событие A уже наступило, то по формуле Байеса:



Задача 4.2. Устройство состоит из 8 независимо работающих элементов. Вероятности отказов каждого из элементов за время Т равны 0,2. Найти: а) вероятность отказа устройства, если для этого достаточно, чтобы отказали хотя бы три элемента; б) наивероятнейшее число отказавших элементов.

Решение. а) Вероятность того, что в n опытах событие A появится k раз (если вероятность появления события А в одном опыте постоянна и равна р) определяется по формуле Бернулли: В данном случае n=8, k=3, 4,...,8, т.е. требуется найти вероятность

.

Вычисления:

0,3355,

P₈(2)= 0,2936, P₈(k3)=1–(0,1678+0,3355 +0,2936) =0,2031. б) np–q = 80,2–0,8=0,8. Следующим за np–q целым числом будет 1, т. е. наивероятнейшее число отказавших за время Т элементов k₀=1. 

ПЗ 5. Предельные теоремы для формулы Бернулли. Простейший поток событий.

Формулой Бернулли при больших n (n>30) практически невозможно воспользоваться в связи с большим объемом вычислительной работы. В таких ситуациях рекомендуется использовать теоремы Лапласа (локальную и интегральную) и теорему Пуассона, позволяющие при больших n приближенно находить вероятности событий, связанных с повторением опытов. Условия применения теорем рассмотрены в лекции 3, п. 3.2. С помощью формулы (3.7) лекции 3 можно обосновать, в некотором смысле, статистическое определение вероятности. Аналог формулы Пуассона используется при подсчете вероятностей, связанных с простейшим потоком событий (лекции 3, п. 3.3).

Решение типовых задач.

Задача 5.1. Вероятность изготовления изделия высшего качества равна 0,8. Изготовлено 64 изделия. Найти: а) наивероятнейшее число изделий высшего качества и вероятность такого числа изделий высшего качества; б) вероятность того, что изделий высшего качества будет изготовлено не менее 50.

Решение. а) В рассматриваемом случае n=64, p=0,8, q=0,2, np–q=640,8–0,2=51,2-0,2=51, т. е. наивероятнейшее число изделий высшего качества k₀=51 (или k₀=52). Находим вероятность P₆₄(51)= P₆₄(52). Так как n=64–достаточно большое число и npq=10,24>9, можно воспользоваться локальной теоремой Лапласа

В данном случае По таблице (приложение 1) (0,25)=0,3867, P₆₄(52)=0,3867/3,2=0,1208; б) Вероятность того, что количество изделий высшего качества будет не менее 50-ти можно найти по интегральной теореме Лапласа

, ,

, .

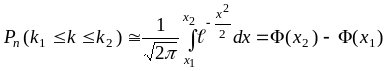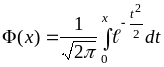По таблице функции (приложение 2) , 0,49997. Тогда 

Задача 5.2. Вероятность появления успеха в каждом из 625 независимых испытаний равна 0,8. а) Найти вероятность того, что относительная частота появления успеха отклонится по абсолютной величине от его вероятности не более чем на 0,04. б) Сколько следует провести опытов, чтобы с вероятностью не меньшей 0,95 можно было ожидать, что относительная частота появления успеха отклонится по абсолютной величине от его вероятности не более чем на 0,02?

Решение. а) Искомую вероятность находим по формуле

б) Обозначим . По условию 2(х)=0,95, (х)=0,475. По таблице функции (х), х=1,96. Из равенства при  =0,02, p=0,8, q=0,2, х=1,96 находим, что т. е. n  1537. 

Задача 5.3. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,002. Найти вероятность того, что в течение одной минуты обрыв произойдет не более чем на двух веретенах.

Решение. Р₁₀₀₀(k2) = Р₁₀₀₀(0) + Р₁₀₀₀(1) + Р₁₀₀₀(2). В данном случае р=0,002<1, np =2, npq=20,998 = 1,996<9 и можно применить формулу Пуассона: Тогда



Задача 5.4. При работе прибора поток неисправностей можно считать простейшим. Среднее число неисправностей за сутки равно 2. Найти вероятности того что: а) за одни сутки не будет ни одной неисправности; б) за двое суток возникнет хотя бы одна неисправность.

Решение. Для простейшего потока событий вероятность того, что за время t произойдет k событий определяется формулой Пуассона , где  – среднее число событий, происходящих в единицу времени. а) =2, t=1, k=0, б) =2, t=2, k1, P₂(k1)=1–P₂(0)=1– 

ПЗ 7. Одномерные дискретные СВ.

Основные определения и формулы, связанные с понятием дискретной СВ, содержаться в лекции 4. Напоминаем, что СВ Х называется дискретной, если в результате опыта она принимает некоторое значение из конечного или счетного множества _Х=x₁, x₂,..., x_n,..,. Для задания дискретной СВ Х достаточно указать множество ее значений _Х и вероятности P(X=x_i), с которыми каждое значение принимается. При этом должно соблюдаться условие где сумма берется по всем значениям СВ Х. Таблица, в которой перечислены в возрастающем порядке значения СВ Х и соответствующие им вероятности, называется законом (или рядом) распределения СВ Х. Числовые характеристики и формулы для их нахождения разобраны в лекции 4, п. 4.2. Рекомендуется предварительно разобрать решение примера 4.2. Понятие функции распределения и метод ее построения рассмотрены в лекции 5, п. 5.1.