Решение типовых задач.

Задача 3.1. По мишени производится три выстрела. Введем события A_i – «попадание при i-м выстреле», i = 1, 2, 3. Выразить через A_i следующие события:

B – «все три попадания»;	C – «все три промаха»;
D – «хотя бы одно попадание»;	E – «хотя бы один промах»;
F – «ровно одно попадание»;	G – «ровно два попадания»;
H – «не менее двух попаданий»;	P – «менее двух попаданий».

Решение. Одновременное наступление нескольких событий – их произведение; наступление хотя бы одного из событий – их сумма. Тогда

Событие F может произойти следующим образом: «А₁ произошло но при этом А₂ и А₃ не произошли» или «А₂ произошло А₁ и А₃ не произошли» или «А₃ произошло А₁ и А₂ не произошли». Аналогично определяется G, т. е.

Событие H означает два попадание или три попадания, т. е. H=G+B. Аналогично P=C+F. 

_{Задача 3.2. Электрическая цепь составлена по схеме, приведенной на рисунке. Выход из строя элемента k – событие Ak (k=1, 2, 3, 4). Записать выражения событий A и B, где A–разрыв цепи, B противоположно А.}

Решение. Введем два блока: b₁ –параллельно соединенные элементы 1 и 2: b₂ – последовательно соединенные элементы 3 и 4. События B₁ (B₂) будут означать,

1

2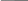

4

3

Рисунок к задаче 3.2.

что блок b₁(b₂) не пропустит электрический ток. При этом В₁=А₁А₂, В₂=А₃+А₄. Тогда А= В₁В₂= А₁А₂(А₃+А₄). По законам дополнения лекция 1, п. 1.4 е15., е16.,



_{Задача 3.3. Две одинаковые монеты радиуса r расположены внутри круга радиуса R (R>2r) и не перекрываются. В круг бросается шарик. Определить вероятность события А – «шарик попадет в одну из монет».}

_{Решение. Введем события А1(А2) – шарик попал в 1-ю(2-ю) монету. Событие А=А1+А2. Так как события А1 иА2 несовместны (шарики не перекрываются) то Р(А)=Р(А1)+Р(А2)= }

_{Задача 3.4. На 10-ти карточках написаны буквы А, А, А, Е, И, К, М, М, Т, Т. Вытаскиваются по одной 4 карточки и выкладываются в порядке появления. Какова вероятность, что получится слово МАМА?}

_{Решение. Пусть событие В – «получилось слово МАМА». Его можно представить в виде произведения В= В1 В2 В3 В4, где В1 – появление буквы М при 1-м вытаскивании карточки, В2 – появление буквы А при 2-м вытаскивании карточки, В3 – появление буквы М при 3-м вытаскивании карточки В4 – появление буквы А при 4-м вытаскивании карточки. По теореме умножения вероятностей}

_{Р(В) = Р(В1)Р(В2/В1)Р(В3/В1В2)Р(В4/В1В2В3)= }

Задача 3.5. Вероятности изготовления деталей 1-го сорта для 1-го, 2-го и 3-го автоматов соответственно равны 0,6, 0,7 и 0,5. С каждого автомата взяли по одной детали. Найти вероятности следующих событий: А – все три детали 1-го сорта; В – хотя бы одна деталь 1-го сорта; С – одна деталь 1-го сорта.

Решение. Введем события А_i – взята деталь 1-го сорта с i-го автомата (i=1, 2, 3). А, В и С представляются в виде: А=А₁А₂А₃, В = А₁ + А₂ + А₃, События А_i можно считать независимыми. По теореме умножения вероятностей независимых событий Р(А)= Р(А₁) Р(А₂) Р(А₃)= 0,60,70,5=0,21. Вероятность события В будем искать переходом к противоположному событию: , Так как событие С представлено в виде суммы несовместных слагаемых и каждое слагаемое является произведением независимых событий, то по теоремам сложения и умножения вероятностей

Р(С)=0,6(1–0,7)(1–0,5)+(1–0,6)0,7(1–0,5)+(1–0,6)(1–0,7)0,5=0,29. 

ПЗ 4.Основные вероятностные формулы.

При решении задач используются: формула полной вероятности и формула Байеса (лекция 2, п. 2.3); формула Бернулли, наивероятнейшее число наступлений события при повторении опытов (лекция 3, п. 3.1).