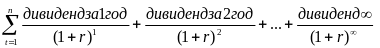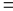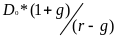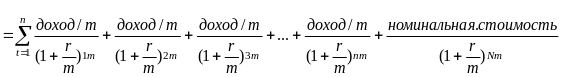X. Финансовый менеджмент Модели оценки доходности финансовых активов

Модель оценки доходности финансовых активов (САРМ) описывает зависимость между рыночным риском и требуемой доходностью. САРМ базируется на допущениях идеального рынка, на добавлении к допустимому множеству портфелей безрискового актива. Линия рынка капитала отражает зависимость риск-доходность для эффективных портфелей, то есть для портфелей, сочетающих рисковые и безрисковые активы. Линия рынка ценных бумаг отражает зависимость риск-доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме, сложенной с произведением премии за рыночный риск и b - коэффициента акции. Формула определения требуемой инвесторами доходности финансового инструмента имеет вид:

r = r_f + β×(r_m -r_f )

где r_f – безрисковый уровень доходности (risk free);

r_m – среднерыночный уровень доходности.

Коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная бумага, имеющая β-коэффициент, равный 1, копирует поведение рынка в целом. Если значение коэффициента выше 1, реакция ценной бумаги опережает изменение рынка как в одну, так и в другую сторону. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы, β-коэффициенты которых ниже 1 (но выше 0). Концепция β-коэффициентов составляют основу модели оценки финансовых активов (Capital Assets Pricing Model, CAPM). При помощи этого показателя может быть рассчитана величина премии за риск, требуемой инвесторами по вложениям, имеющим систематический риск выше среднего.

Считается, что инвесторы питают неприязнь к излишнему на их взгляд риску, поэтому любая ценная бумага, отличная от безрисковых государственных облигаций или казначейских векселей, может рассчитывать на признание инвесторов только в том случае, если уровень ее ожидаемой доходности компенсирует присущий ей дополнительный риск. Данная надбавка называется премией за риск напрямую зависит от величины β-коэффициента данного актива, так как предназначена для компенсации только систематического риска. Несистематический риск может быть устранен самим инвестором путем диверсификации своего портфеля, поэтому рынок не считает нужным устанавливать вознаграждение за этот вид риска.

Сама по себе CAPM является изящной научной теорией, имеющей солидное математическое обоснование. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие трансакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β-коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель.

В качестве альтернативы традиционной однофакторной модели САРМ можно назвать модель арбитражного ценообразования (Arbitrage Pricing Model, АРМ). В основе модели утверждение о том, что рисковая доходность определяется многими экономическими факторами (рыночная ситуация в стране, стабильность мировой экономики, инфляция, динамика процентных ставок и т.д.). Таким образом, модель должна включать множество факторов и в наиболее общем виде описывается зависимостью:

k_i = k_RF + (λ₁ - k_RF)b_i1 + … + (λ_j - k_RF)b_ij + е_i

где λ_j – требуемая доходность портфеля с единичной чувствительностью к j-му экономическому фактору (b_j = 1) и нулевой чувствительностью (b_j = 0), к другим факторам;

е_i – влияние не включённых в модель специфических факторов на изменение доходности i-й ценной бумаги;

b_ij – чувствительность доходности i-го актива к j-му фактору.

Данная модель обладает достоинствами и недостатками. Основным недостатком является то, что она не предусматривает жёстких исходных предпосылок, которые свойственны модели САРМ, количество и состав релевантных факторов определяются аналитиком и заранее не регламентируются. Фактическая реализация модели связана с использованием сложного процесса математической статистики. Тем не менее, главное достоинство этой теории в том, что доходность является функцией многих переменных и рассматривается среди учёных как одна из перспективных.

Оценка акций и облигаций. Расчет доходности акций и облигаций

Существуют три основных вида стоимости акций: номинальная, эмиссионная и рыночная.

На акции указывается номинальная стоимость, определяемая как:

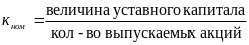
Номинальная стоимость акции выступает ориентиром для определения эмиссионной цены и рыночной цены, а также размера дивиденда. Если акция приобретается у эмитента, то стоимость называется эмиссионной, если на вторичном рынке, то - рыночной.

Эмиссионная стоимость может совпадать с номиналом или откланяться в ту или иную сторону. Рыночная стоимость определяется спросом и предложением.

Рыночная стоимость акции в расчете на 100 денежных единиц номинала называется курсом.

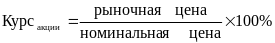
Получение доходов по обыкновенным акциям характеризуется неопределенностью, как в плане величины, так и времени их получения. Теоретически стоимость обыкновенных акций рассчитывается по формуле:

Текущая стоимость обыкновенных акций

=

Если же ожидается, что диви­денды компании будут расти одинаковыми темпами в будущем, то для расчета текущей стоимости обыкновенной акции используется формула Гордона:

Текущая стоимость обыкновенных акций

где 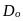– базовая величина дивидендов (в руб.);

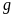– темп роста дивидендов (в %);

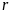– требуемая норма доходности инвестора (в %).

Текущая доходность акции для инвестора определяется рендитом (т.е. ставкой текущего дохода). Рендит характеризует, сколько рублей дохода получено акционером на каждый инвестированный рубль.

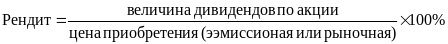
Текущая рыночная доходность акции рассчитывается по формуле:

Доходность акции в среднегодовом исчислении определяется по формуле:

К_ср =

	(Цена продажи – цена покупки): кол-во лет	+	Средняя величина доходов	×100%
	Цена покупки

Конечная доходность (совокупная) по акции определяется по формуле:

Ккон =	(Цена продажи – цена покупки)	+	Дивиденды за период владения	×100%
	Цена покупки

Рыночную (курсовую) цену акции можно определить по формуле:

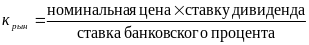
При анализе привилегированных акций в расчетах используют собственную норму прибыли инвестора, показывающую максимальную цену, которую инве­стор готов заплатить за акции, или минимальную цену, за которую инвестор готов продать эту акцию.

Для определения текущей стоимости привилегированных акций используется формула:

Текущая стоимость привилегированных облигаций

=

Объявленный уровень дивидендов

:

Требуемая норма прибыли инвестора (в % или долях)

Текущая стоимость облигаций состоит из двух частей:

– дисконтированная стоимость, полученная до даты погашения процентных платежей;

– дисконтированная стоимость выплаты номинала при наступлении срока погашения.

Номинальная стоимость облигации определяются как:

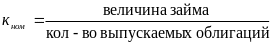
Формула для определения текущей рыночной цены об­лигаций (PV) с фиксированным купоном имеет следующий вид:

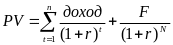
где F – сумма, выплачиваемая при погашении облигации (номинальная стоимость);

t – год;

r – ставка дисконта или требуемая инвестором норма дохода;

n – число лет оставшихся до момента погашения облигации;

N – последний год срока погашения.

Если купонные платежи не фиксированы, то поступления процентных платежей каждый год меняются. Поскольку каждый процентный платеж отличен от других, то он должен рассматриваться как самостоятельный единовре­менный платеж. Следовательно, формула расчета текущей стоимости облигации с плавающим купоном имеет следующий вид:

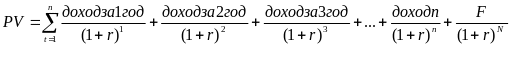
Также существует бескупонная облигация, т.е. купонные платежи по ней равны нулю, тогда текущая стоимость такой облигации определяется по формуле:

При выплате доходов по облигациям несколько раз в год текущая стоимость определяется по формуле:

Текущая стоимость облигации		=

где m – частота выплат процентов в год.

Если известна курсовая цена облигации и величина процентного дохода, то можно определить текущую рыночную доходность облигации по формуле:

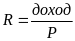
где Р – рыночная цена облигации; доход = Номинал × купон.

Конечная доходность (совокупная) по облигации определяется по формуле:

Ккон =	(Цена продажи или номинал цена покупки)	+	Совокупный купонный доход	×100%
	Цена покупки

Купонная доходность при эмиссии облигации определяется как:

К=