
Алгоритм решения системы линейных уравнений методом Гаусса
1. Составить расширенную матрицу системы линейных уравнений (1) и с помощью элементарных преобразований привести к ступенчатому виду.
2. Провести исследование:
а)
если
![]() ,
то система (1) несовместна;
,
то система (1) несовместна;
б)
если
![]() ,
то система (1) совместна. При этом,
,
то система (1) совместна. При этом,
если r=n, то система (1) определена,
если r<n, то система (1) неопределена.
3. Найти решение системы уравнений, которая соответствует полученной ступенчатой матрице.
Задание 1. Вычислить А+В, А-В, n∙А, tB, А∙В, В∙А:
 ,
,
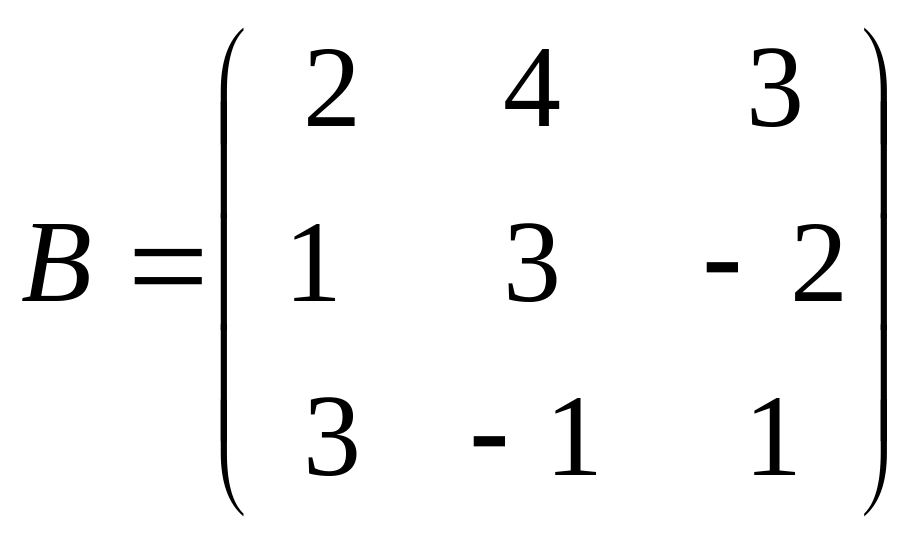 ,
n=5.
,
n=5.
Решение:
Пусть
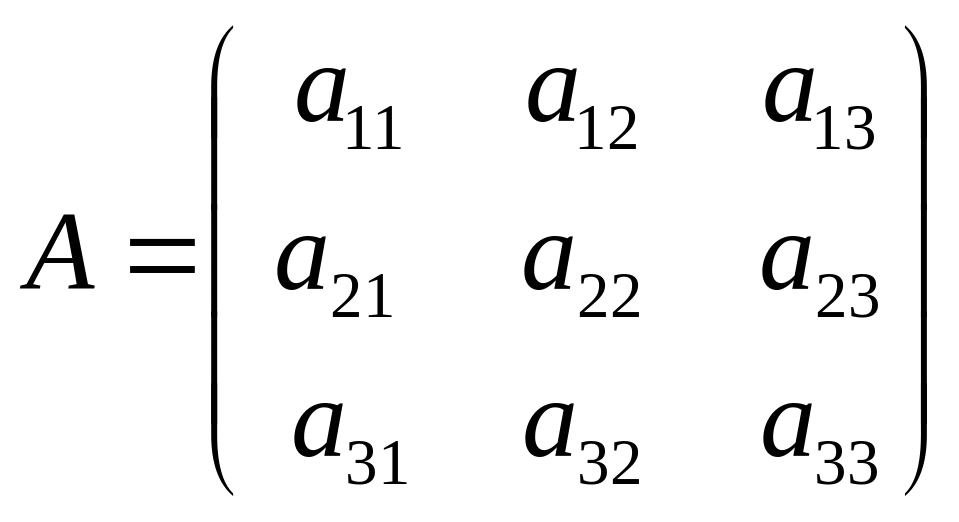 ,
,
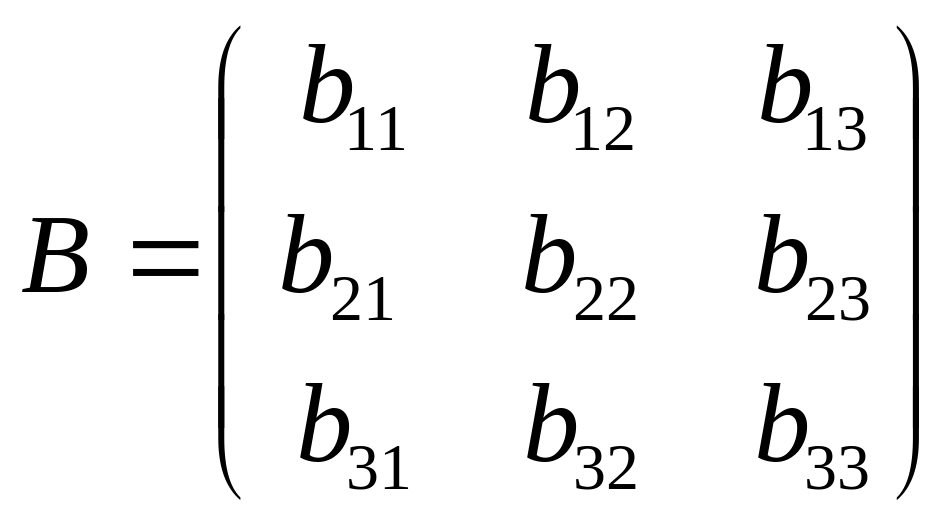 .
Тогда,
.
Тогда,
ввиду
определений 2.6 и 2.7 (см.
стр.35):
 ;
;
 ;
;
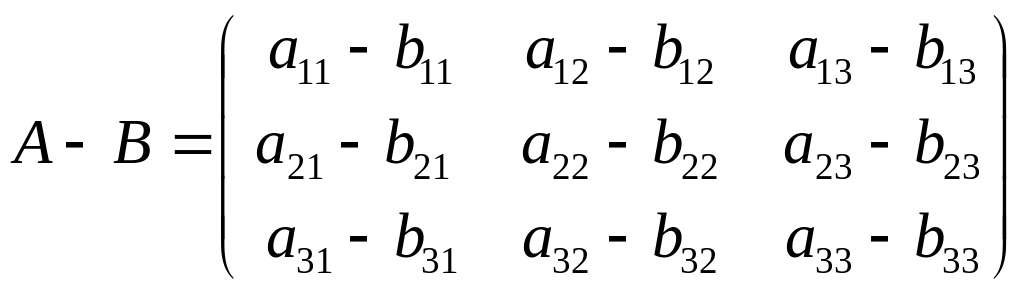 .
По определению 2.9,
.
По определению 2.9,
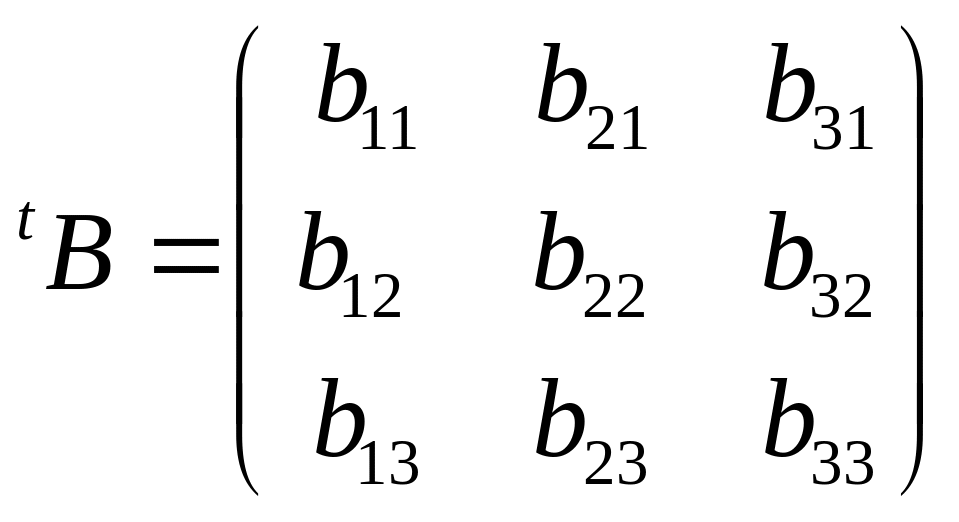 .
Согласно определению 2.8,
.
Согласно определению 2.8,
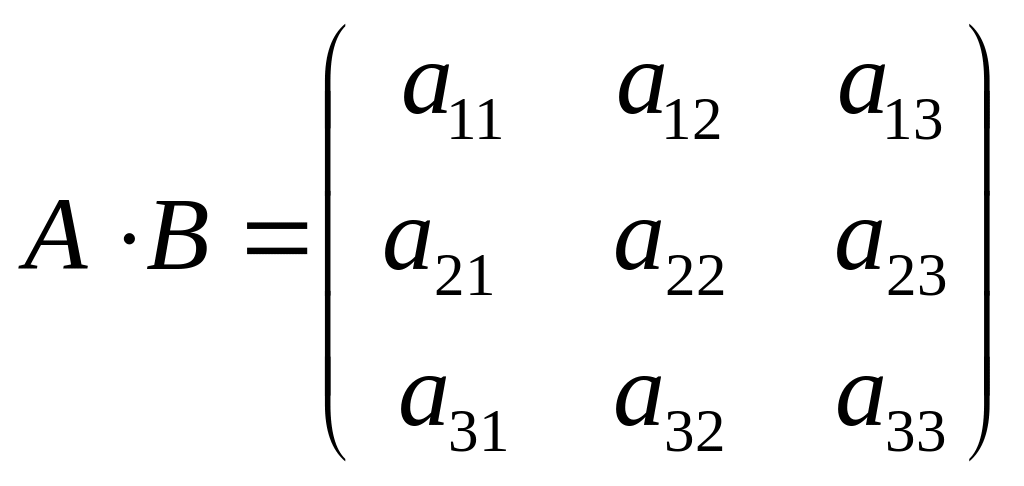 ∙
∙ =
=
=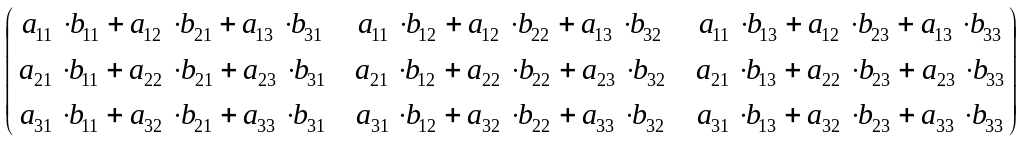 ;
;

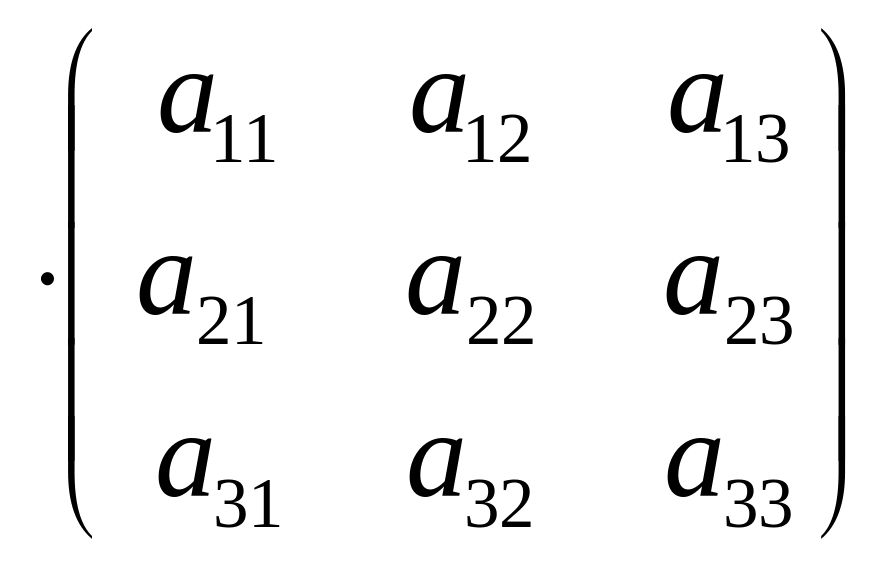 =
=
=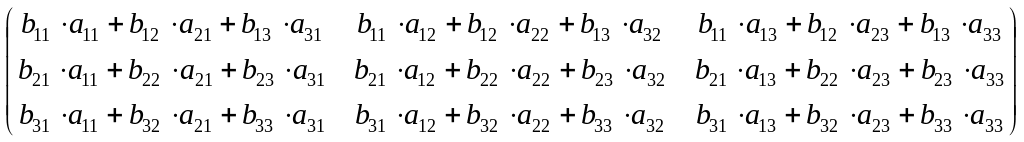 .
.
Таким образом, получаем
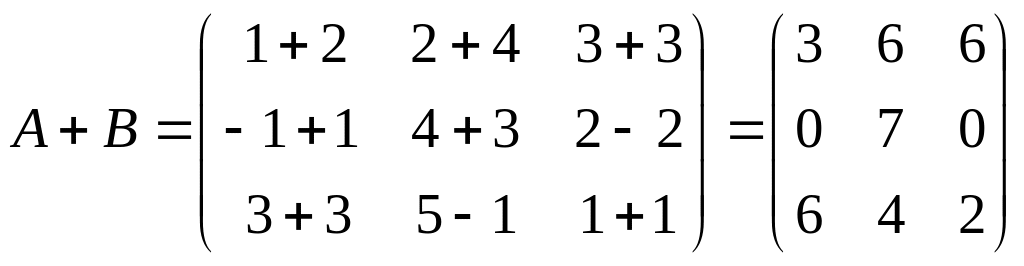 ,
,
 ,
,
 ,
,
 ,
,
 ∙
∙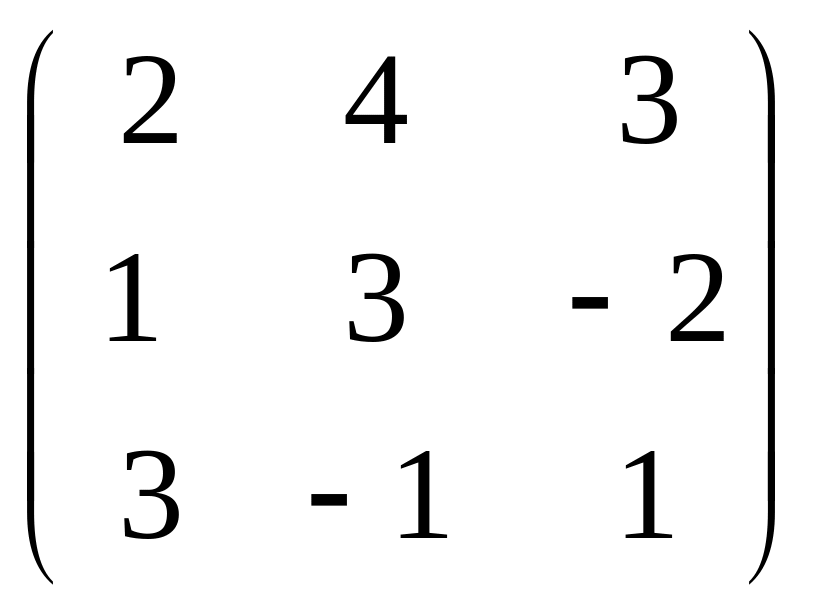 =
=
= ,
,
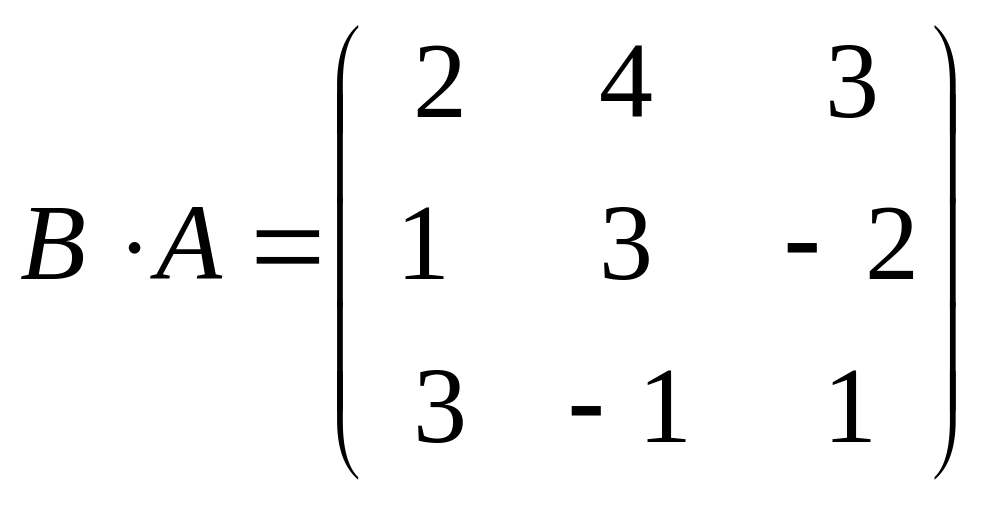
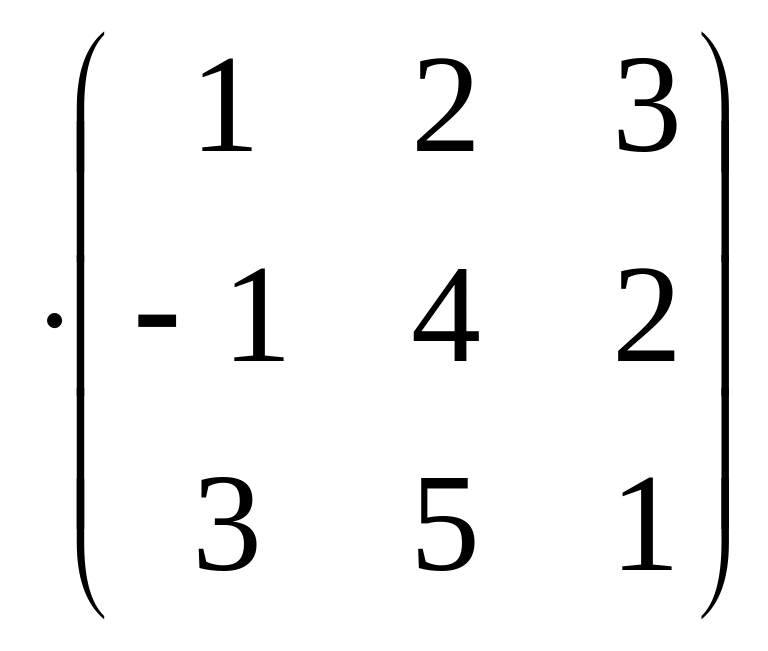 =
=
=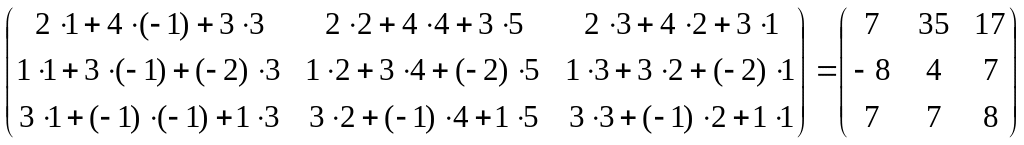 .
.
Ответ:
 ,
,
 ,
,
 ,
,
,
![]()
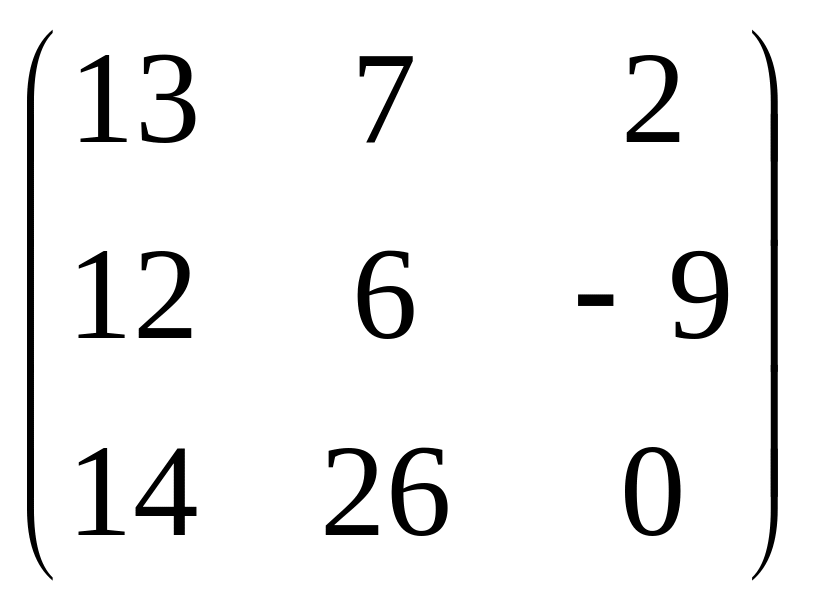 ,
,
![]()
 .
.
Задание 2. Вычислить определитель матрицы А из задания 1 двумя способами: а) по правилу Саррюса; б) разложением по ряду.
Решение:
а) Согласно правилу Саррюса (см. стр.
40), определитель 3-го порядка равен сумме
шести слагаемых:

![]()






 • • •
• • •
• • •
• • •

 • • •
• • •
• • •
• • •
• • • • • •
Таким образом,
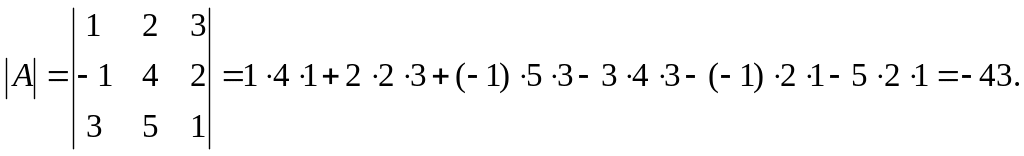
б) Вычислим определитель матрицы А с помощью разложения определителя по ряду. Согласно формуле (1) (см. стр. 40), разложение определителя матрицы А по i-й строке имеет вид:
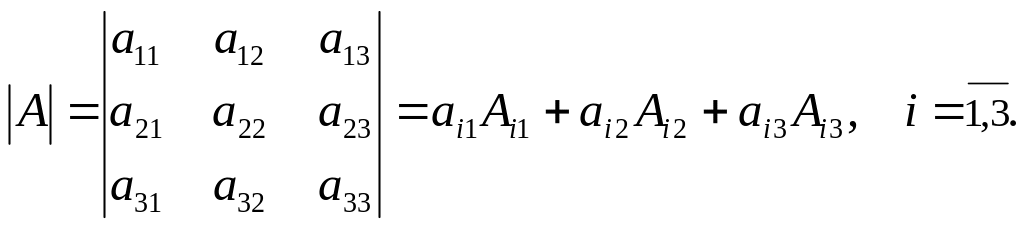
Согласно формуле (2) (стр. 40), разложение определителя матрицы А по j-му столбцу имеет вид:

Отметим,
что Aij
– алгебраическое дополнение к элементу
аij в
определителе
![]() (см. стр. 40, определение 2.15). По теореме
2.1 (стр. 41) Aij
вычисляют по формуле Aij=(-1)i+
j ∙Mij
, где Mij
– минор к элементу аij
в определителе
(см. стр. 41, определение 2.16), i
=
(см. стр. 40, определение 2.15). По теореме
2.1 (стр. 41) Aij
вычисляют по формуле Aij=(-1)i+
j ∙Mij
, где Mij
– минор к элементу аij
в определителе
(см. стр. 41, определение 2.16), i
=
![]() ,
j =
.
,
j =
.
Вычислим определитель матрицы А, например, с помощью разложения по 3-й строке:
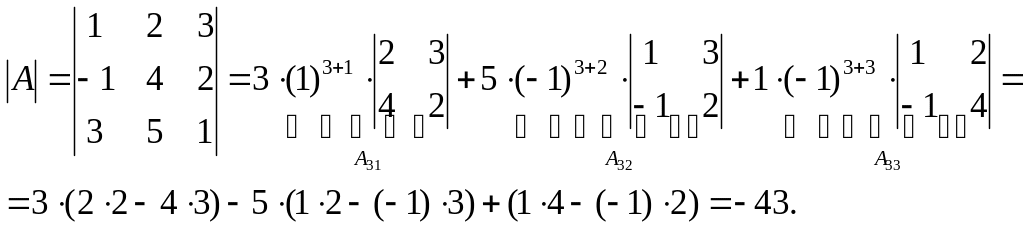
Отметим,
что
![]() (см. стр. 39).
(см. стр. 39).
Ответ: =-43.
Задание 3. Для матрицы В из задания 1 найти обратную матрицу
В-1 двумя способами: а) с помощью элементарных преобразований;
б) с помощью алгебраических дополнений.
Решение:
Предварительно установим, является ли матрица В обратимой. Ввиду теоремы 2.2 (см. стр. 41), достаточно найти определитель матрицы В:
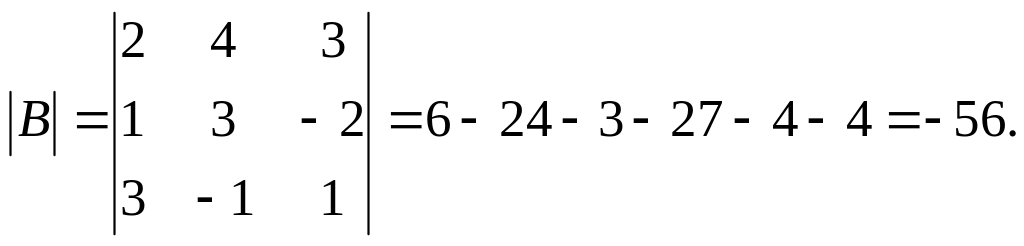
Так как
![]() ,
то, согласно теореме 2.2, матрица В-1
существует.
,
то, согласно теореме 2.2, матрица В-1
существует.
а) Вычислим матрицу В-1
с помощью элементарных преобразований.
Для этого запишем расширенную матрицу
вида
![]() и с помощью элементарных преобразований
(см. стр. 43, определение 2.25) приведем
подматрицу В в ней к единичной
матрице En.
Тогда в правой части полученной
расширенной матрицы будет находиться
матрица В-1:
и с помощью элементарных преобразований
(см. стр. 43, определение 2.25) приведем
подматрицу В в ней к единичной
матрице En.
Тогда в правой части полученной
расширенной матрицы будет находиться
матрица В-1:
![]() ∼
…∼
∼
…∼![]() .
.
Таким образом,









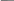
 ∼
∼

∼



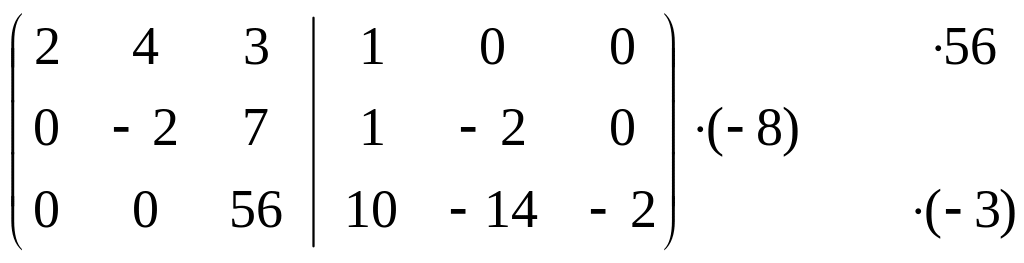 ∼
∼
∼
 ∼
∼
∼

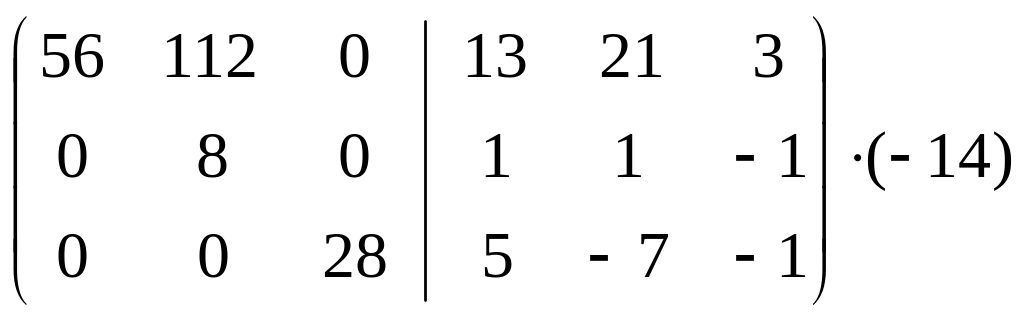 ∼
∼
 ∼
∼
∼ . Отсюда следует, что В-1=
. Отсюда следует, что В-1= ,
т.е.
,
т.е.
В-1= .
.
б)
Вычислим матрицу В-1
с помощью алгебраических дополнений.
Согласно теореме 2.3
(стр. 41), В
=
![]() ∙
∙
 ,
,
где
Аij
-
алгебраическое дополнение к элементу
аij
в матрице В, i=![]() ,
j=
.
Таким образом, ввиду теоремы 2.1,
,
j=
.
Таким образом, ввиду теоремы 2.1,
![]()
![]()
![]()
Тогда
В-1=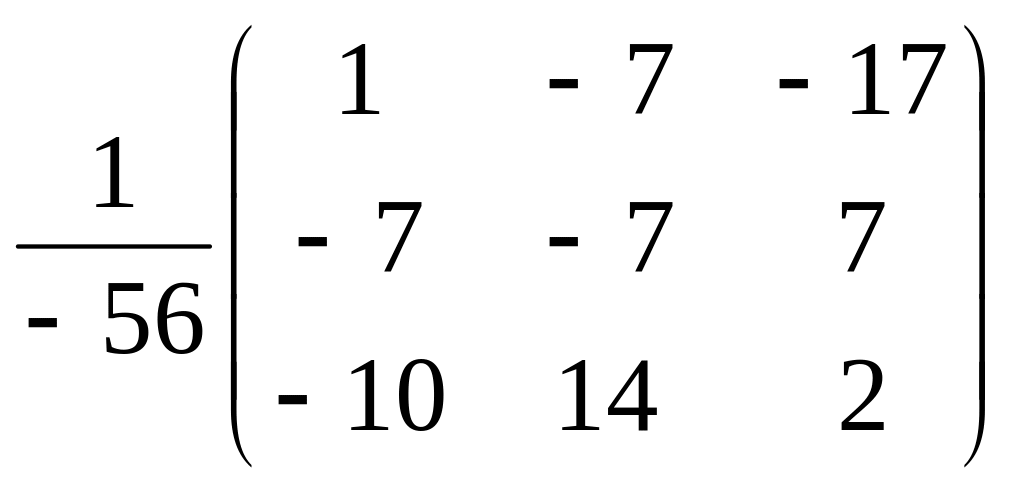 =
.
=
.
Ответ: В-1= .
Задание 4. Решить систему линейных уравнений двумя способами: а) по правилу Крамера; б) матричным способом:
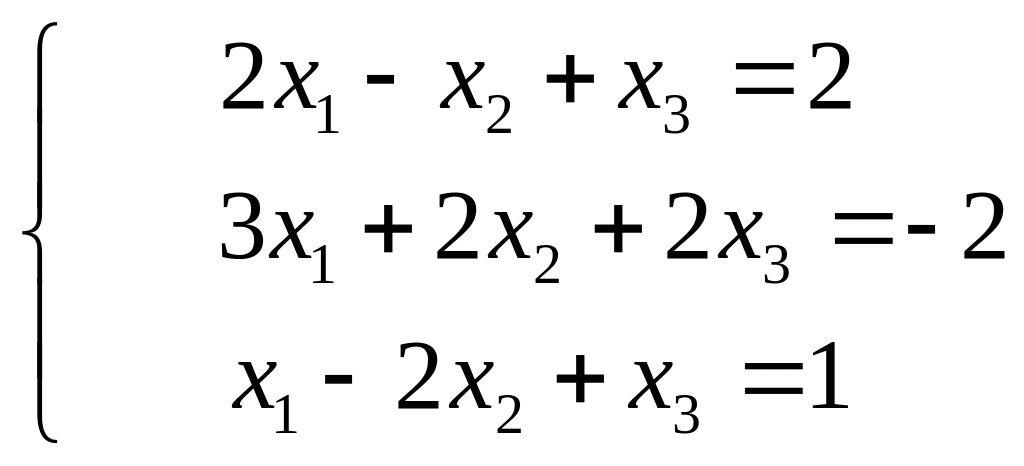 (1).
(1).
