Матрицы и определители

М а т р и ц ы

Определение 2.1. Матрицей размера m n над полем Р называется прямоугольная таблица, состоящая из m строк и n столбцов, следующего вида:

, где a_ij P, i= , j= .

Матрицы также можно обозначать следующим образом:

А=(a_ij), i= , j= , или

А=||a_ij||, i= , j= .

Определение 2.2. Квадратной матрицей n-го порядка над полем P называется матрица размера n n над полем P.

Пусть A – квадратная матрица n-го порядка над полем P. Тогда в матрице А выделяют две диагонали: главную и побочную:

главная побочная

Строки матрицы А называют вектор-строками и обозначают следующим образом:

А_i – i-я вектор-строка матрицы А, т.е. А_i=(a_i1, a_i1, _… ,a_in) = .

Столбцы матрицы А называют вектор-столбцами и обозначают следующим образом:

А^j – j-й вектор-столбец матрицы А, т.е. А^j = = .

Определение 2.3. Две матрицы А и В размера m n над полем P называются равными и обозначаются А=В, если в А и В элементы, стоящие на соответствующих местах, равны, т.е. a_ij=b_ij, i= , j= .

Определение 2.4. Матрица над полем P называется нулевой и обозначается θ, если все ее элементы равны нулю, т.е. = .

Определение 2.5. Матрица n-го порядка над полем P называется единичной и обозначается E_n, если в ней на главной диагонали находятся единицы, а на остальных местах – нули, т.е.

E_n = .

Операции над матрицами

1) Сложение матриц.

Определение 2.6. Пусть A=(a_ij), B=(b_ij) - матрицы размера m n над полем Р. Матрица С=(c_ij) размера m n над полем Р называется суммой матриц А и В и обозначается С=А+В, если c_ij=a_ij+b_ij, i= , j= .

Другими словами, сложение матриц одинакового размера сводится к сложению их элементов, стоящих на соответствующих местах.

2) Умножение матрицы на скаляр.

Определение 2.7. Пусть A=(a_ij) – матрица размера m n над полем P, P. Матрица С=(с_ij) размера m n над полем P называется произведением матрицы А на элемент и обозначается С= ^.А, если с_ij= ^.a_ij , j= , i= .

Другими словами, чтобы умножить матрицу А над полем Р на элемент α∈Р, необходимо каждый элемент матрицы А умножить на α.

3) Умножение матриц.

Определение 2.8. Пусть A=(a_ij) – матрица размера m n над полем P, B=(b_ij) - матрица размера n k над полем P. Матрица С=(с_ij) размера m k над полем P называется произведением матриц А и В и обозначается С=A∙B, если элемент с_ij равен скалярному произведению i-й вектор-строки матрицы А на j-й вектор-столбец матрицы B, т.е.

с_ij=A_i∙B ^j=(a_i1,...,a_in)∙ = a_i1b_1j+^…+a_inb_{nj =} , i= , j= .

4) Транспонирование матрицы.

Определение 2.9. Пусть A - матрица размера m n над полем P. Транспонированием матрицы А называется операция замены в матрице А i-й строки на i-й столбец, i= . Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается ^tA.

Обратимые матрицы. Матричные уравнения.

Определение 2.10. Матрица А n-го порядка над полем Р называется обратимой, если существует такая матрица В над полем Р, что АВ=ВА=Е_n. Матрица В называется матрицей, обратной для матрицы А, и обозначается А^-1.

Простейшие матричные уравнения имеют вид:

1) A∙X=B, 2) X∙A=B, 3) A∙X∙B=C, где А, В, С – некоторые матрицы.

Если матрица А^-1 существует, то

в случае 1): X=A^-1 ∙B,

в случае 2): X=B∙A^-1,

в случае 3): X∙B=A^-1 ∙C.

При этом, если матрица B^-1 существует, то в случае 3) X=A^-1 ∙C∙B^-1.

П е р е с т а н о в к и n - й с т е п е н и

Определение 2.11. Пусть М={1,2,…,n}. Перестановкой на множестве М или перестановкой n-й степени называется множество М с заданным расположением его элементов, и обозначается I=(i₁i₂…i_n), где i₁,i₂,..,i_n – попарно различные элементы из М.

Например, пусть М={1,2,3}. Тогда перестановки на М имеют вид: I₁=(132), I₂=(231), I₃=(123) и т.д.

Определение 2.12. Инверсией или беспорядком перестановки I называется любая пара символов перестановки I, в которой символ, стоящий левее, больше символа, стоящего правее.

Например, в перестановке I₂=(231) две инверсии: 31 и 21.

Через (I) обозначается число всех инверсий перестановки I.

Пример 2.1. Пусть I=(312465). Тогда перестановка I имеет три инверсии 31, 32, 65, т.е. (I)=3.

Определение 2.13. Перестановка I называется чётной, если (I) – чётное число, в противном случае перестановка I называется нечётной.

В примере 2.1 перестановка I – нечётная.

Через S_n обозначается множество всех перестановок n-ой степени.

Утверждение 2.1. | S_n |=n! .

О п р е д е л и т е л и

Пусть А= - матрица n-го порядка над полем Р.

Из элементов матрицы А будем составлять всевозможные произведения, состоящие из n множителей, любые два различных из которых находятся в разных строках и разных столбцах. Таким, например, является произведение элементов, стоящих на главной диагонали: a₁₁a₂₂…a_nn. Все такие произведения можно получить по следующему правилу: выберем для произведения из первой строки матрицы А некоторый элемент , затем вычеркнем первую строку и j₁-й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент и т.д. Через конечное число шагов получим произведение вида: … .

Так как j₁,j₂,…,j_n – попарно различные элементы из множества М={1,2,…,n}, то вторые индексы в записанном произведении образуют перестановку I=(j₁j₂…j_n).

Рассмотрим выражение вида: (-1) ^(I)∙ (1), где I=(j₁j₂…j_n).

Выражений вида (1) можно образовать столько, сколько существует перестановок, составленных из вторых индексов, т.е., ввиду утверждения 2.1, их будет n!.

Определение 2.14. Пусть А= - матрица n-го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент поля Р, равный

.

Для определителя n-го порядка используются следующие обозначения: = 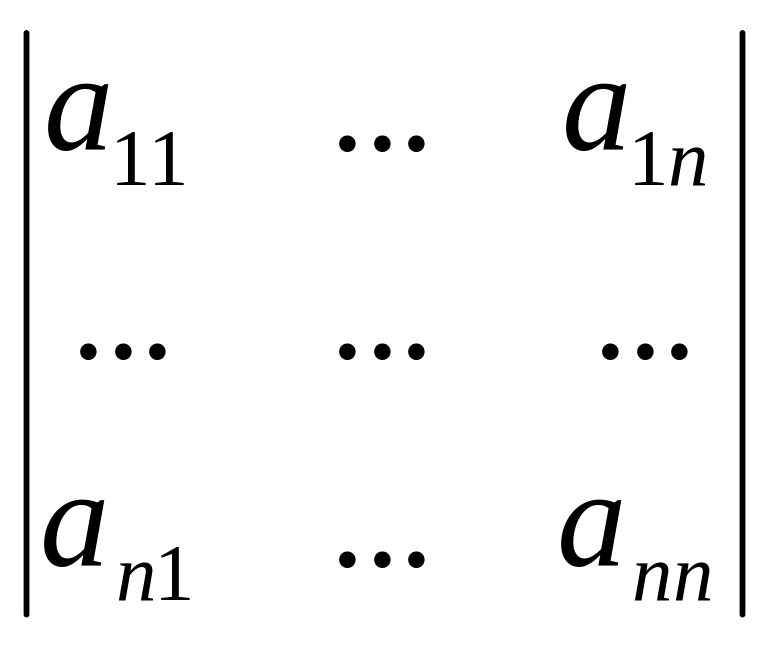, =|A|, =|a_ij|, i= , j= , =detA ( - читается «дельта»).

1) Пусть Δ – определитель 2-го порядка, т.е.

Δ = = .

Отметим, что = 2! = 2; M = .

Так как I₁ = (12), то = 0 ,

I₂ = (21), то = 1 , и значит,

Δ = = .

Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

2) Пусть Δ - определитель 3-го порядка:

Δ = = .

Отметим, что |S₃|= 3! = 6; M = . Тогда

I₁ = (123) = 0 ;

I₂ = (213) = 1 ;

I₃ = (312) = 2 ;

I₄ = (321) = 3 ;

I₅ = (132) = 1 ;

I₆ = (231) = 2 .

Следовательно,

Δ= = .

Таким образом, определитель 3-го порядка равен сумме шести слагаемых, три из которых со знаком +:

- произведение элементов на главной диагонали,

- произведение элементов на диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу,

- произведение элементов второй диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу;

Остальные три слагаемых получают аналогично, только рассуждения проводят для побочной диагонали.

Записанное правило называют правилом Саррюса.

Определение 2.15. Пусть Δ = . Если в определителе Δ сгруппировать все слагаемые, содержащие элемент , и сгруппировав, вынести элемент за скобки, то выражение, полученное в скобках, обозначается A_ij и называется алгебраическим дополнением к элементу в определителе Δ, i = , j = .

Т ак как все элементы i-той строки определителя Δ входят в одно и только одно из слагаемых, то Δ=a_i1A_i1+ a_i2A_{i2+ … +} a_inA_in (1).

Равенство (1) называется разложением определителя Δ по i-той строке.

А налогично: Δ=a_1jA_1j+ a_2jA_{2j+ … +} a_njA_nj (2) - разложение определителя Δ по j-тому столбцу, j = .

Строки и столбцы определителя Δ называются его рядами. Таким образом, (1) и (2) – разложения Δ по ряду.

Определение 2.16. Если в определителе Δ = вычеркнуть i-тую строку и j-тый столбец, то на их пересечении получится элемент a_ij, а остальные элементы образуют определитель (n-1)-го порядка, который обозначается M_ij и называется минором к элементу a_ij в определителе Δ, i = , j = .

Например:

Пусть Δ = . Тогда, например, M₂₃ = .

Т еорема 2.1. Пусть Δ - определитель n-го порядка над полем P, A_ij и M_ij – алгебраическое дополнение и минор к элементу a_ij в Δ соответственно. Тогда

A_ij=(-1)^{i+ j} ∙M_ij , i = , j = .

Теорема 2.2. Квадратная матрица А является обратимой тогда и только тогда, когда |A| ≠ 0.

Теорема 2.3. Пусть A= - матрица n-го порядка над полем P, = 0. Тогда

А = ∙ ,

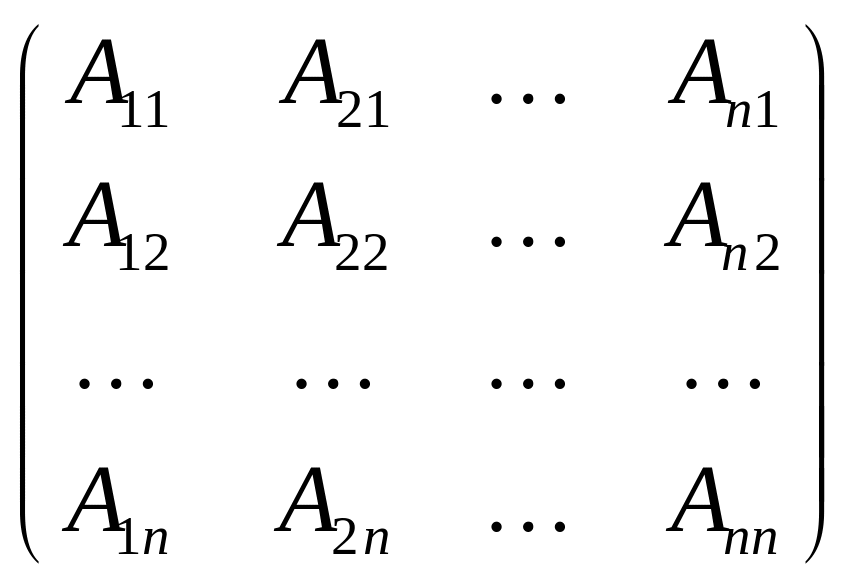где А_ij - алгебраическое дополнение к элементу а_ij в матрице А, i= , j= .