
- •Методичнi рекомендації
- •Методичні рекомендації для самостійного вивчення модуля «Лінійна алгебра та аналітична геометрія»
- •Термінологічний словник.
- •Варіанти індивідуальних завдань.
- •Методичні рекомендації для самостійного вивчення модуля «Комплексні числа. Основи диференціального числення» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Екстремум функції
- •Диференціювання складних функцій з кількома змінними
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Методичні рекомендації для самостійного вивчення модуля «Інтегральне числення.» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Формула Ньютона - Лейбниця для обчислення визначених інтегралів
- •Формули для розв’язування прикладних задач
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Вимоги щодо виконання контрольної роботи
- •Література з вищої математики, що є у бібліотеці коледжу.
Варіанти індивідуальних завдань.
Завдання №1. Подані матриці А та В, числа α та β. Знайти:
а) С=αА + βВ; б) D = А · ВТ ; F = ВТ · А.
У кожному варіанті перша матриця– А, друга – В, перше число – α, друге – β.
1. ,
,
 ,
2, 3 2.
,
2, 3 2. ,
,
 ,
-1, 2
,
-1, 2
3.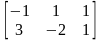 ,
,
 ,
2, 2 4.
,
2, 2 4. ,
,
 ,
4, 3
,
4, 3
5.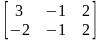 ,
,
 ,
-1, -2 6.
,
-1, -2 6. ,
,
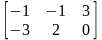 ,
-3, 1
,
-3, 1
7. ,
,
 ,
3, 2 8.
,
3, 2 8. ,
,
 ,
-2, 3
,
-2, 3
9. ,
,
 ,
-2, 4 10.
,
-2, 4 10. ,
,
 2, -2
2, -2
11. ,
,
 ,
4, 4 12.
,
4, 4 12. ,
,
 ,
4, -2
,
4, -2
13.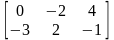 ,
,
 ,
2, 3 14.
,
2, 3 14.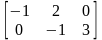 ,
,
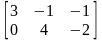 ,
3, 2
,
3, 2
15. ,
,
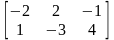 ,
-3, -1 16.
,
-3, -1 16. ,
,
 ,
3, 3
,
3, 3
17.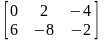 ,
,
 ,
4,2 18.
,
4,2 18. ,
,
 ,
-2, 4
,
-2, 4
19. ,
,
 ,
2, -4 20.
,
2, -4 20.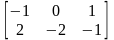 ,
,
 ,
3, -5
,
3, -5
21. ,
,
 ,
4, -3 22.
,
4, -3 22. ,
,
 ,
-1, -2
,
-1, -2
23. ,
,
 ,
2, -2 24.
,
2, -2 24. ,
,
 ,
2, 4
,
2, 4
25. ,
,
 ,
2, 3 26.
,
2, 3 26. ,
,
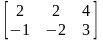 ,
3, -4
,
3, -4
Завдання №2.
Обчислити визначник матриці двома засобами:
а) розкладенням за елементами рядка чи стовпця;
б) методом трикутників;
в) методом Саррюса.
Завдання №3.
Знайти матрицю А-1, якщо матриця А дорівнює:
Варіанти завдання 2 та 3.
1. 2.
2. 3.
3.
4. 5.
5. 6.
6.
7. 8.
8. 9.
9.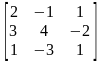
10.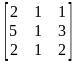 11.
11. 12.
12.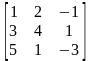
Завдання №4.
Задана матриця А. Знайти її ранг за допомогою елементарних перетворень.
1. 2.
2. 3.
3.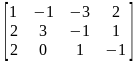
4.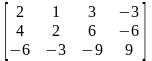 5.
5. 6.
6.
7. 8.
8. 9.
9.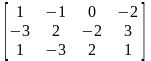
10. 11.
11. 12.
12.
13. 14.
14.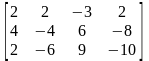 15.
15.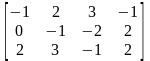
16. 17.
17. 18.
18.
19. 20.
20. 21.
21.
22. 23.
23. 24.
24.
25.
Завдання №5.
Розв’язати систему лінійних рівнянь двома засобами:
а) по правилу Крамера;
б) матричним засобом.
1. 2.
2.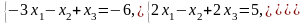 3.
3.
4. 5.
5. 6.
6.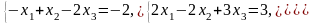
7.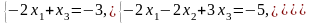 8.
8. 9.
9.
10.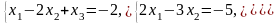 11.
11. 12.
12.
13. 14.
14. 15.
15.
16. 17.
17.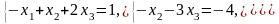 18.
18.
19. 20.
20. 21.
21.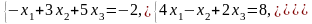
22. 23.
23. 24.
24.
25.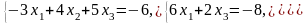 26.
26.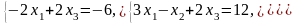 27.
27.
28. 29.
29.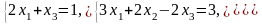 30.
30.
Завдання 6. Задано координати вершини піраміди:
1.
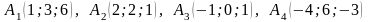 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
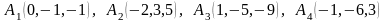 .
.
7.
 .
.
8.
 .
.
9.
 .
.
10.
 .
.
Знайти:
1. Довжину ребра
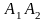 .
.
2.
Кут між ребрами
та
 .
.
3.
Площу грані
 .
.
4. Об’єм піраміди.
5. Зробити креслення.
Завдання №7.
Відомі координати точок А, В, С та D.
1. Знайдіть координати векторів а=АВ, b=CD.
2. Знайдіть їх довжину (абсолютну величину).
3. Знайдіть координати вектора d=2a-b та його абсолютну величину.
4. Знайдіть скалярний добуток векторів а та b.
Дані за варіантами.
1 варіант А(12; 5) В(11; 4) С(1; 1) D(9; 0)
2 варіант А(12; 13) В(4; 12) С(7; 0) D(1; 7)
3 варіант А(0; 2) В(8; 3) С(5; 3) D(5; 0)
4 варіант А(11; 4) В(5; 1) С(3; 8) D(2; 5)
5 варіант А(8; 13) В(8; 12) С(5; 9) D(8; 4)
6 варіант А(7; 9) В(1; 2) С(2; 7) D(5; 5)
7 варіант А(4; 5) В(7; 1) С(1; 6) D(1; 4)
8 варіант А(10; 8) В(9; 2) С(4; 2) D(4; 7)
9 варіант А(13; 7) В(1; 0) С(1; 3) D(5; 5)
10 варіант А(7; 6) В(0; 13) С(8; 9) D(3; 7)
11 варіант А(1; 3) В(6; 3) С(7; 9) D(7; 2)
12 варіант А(1; 9) В(4; 2) С(7; 4) D(5; 2)
13 варіант А(12; 8) В(2; 2) С(5; 8) D(6; 3)
14 варіант А(9; 5) В(8; 14) С(8; 1) D(1; 8)
15 варіант А(11; 14) В(6; 2) С(1; 9) D(3; 3)
16 варіант А(1; 2) В(4; 14) С(1; 9) D(3; 5)
17 варіант А(3; 7) В(6; 13) С(5; 5) D(5; 7)
18 варіант А(5; 5) В(12; 9) С(5; 1) D(1; 6)
19 варіант А(13; 0) В(4; 11) С(0; 9) D(5; 8)
20 варіант А(11; 4) В(6; 8) С(2; 2) D(1; 6)
21 варіант А(13; 14) В(5; 0) С(1; 2) D(8; 2)
22 варіант А(11; 14) В(6; 6) С(4; 8) D(0; 0)
23 варіант А(10; 1) В(1; 7) С(7; 5) D(9; 3)
24 варіант А(9; 10) В(9; 6) С(6; 2) D(3; 2)
25 варіант А(7; 3) В(10; 14) С(1; 2) D(7; 6)
Завдання №8.
Дано координати вершин деякого трикутника АВС. Знайти:
а) рівняння сторони ВС;
б) довжину сторони ВС;
в) рівняння висоти, проведеної з точки А;
г)довжину висоти, проведенної з точки А;
д) рівняння медіани, проведенної з вершини С;
е) площу трикутника АВС;
ж) кут В (у радіанах з точністю до двох знаків).
Зробити малюнок!
1. А(-10; 5) В(14; -2) С(-4; 22)
2. А(-10;10) В(14;; 3) С(-4; 27)
3. А(-20; 1) В(4; -6) С(-14; 18)
4. А(-15; -7) В(9; -14) С(-9; 10)
5. А(-20; 4) В(4; -3) С(-14; 21)
6. А(-10; 12) В(14; 5) С(-4; 29)
7. А(5; 3) В(29; -4) С(11; 20)
8. А(-8; 4) В(16; -3) С(-2; 21)
9. А(-13; 5) В(11; -12) С(-7; 12)
10. А(5; 4) В(-4; 8) С(-9; -2)
11. А(4; 6) В(-4; 0) С(-1; 4)
12. А(-1; 2) В(3; -1) С(0; 4)
13. А(3; 2) В(5; -2) С(1; 0)
14. А(10; 6) В(-2; 2) С(4; -6)
15. А(2; -1) В(-1; 3) С(2; 4)
16. А(-26; -10) В(22; 24) С(-14; 24)
17. А(-3; 3) В(6; -9) С(12; 9)
18. А(1; -1) В(-2; 1) С(3; 5)
19. А(8; 4) В(-4; -4) С(12; 8)
20. А(6; 7) В(-5; 9) С(-10; -3)
21. А(3; 1) В(-5; 8) С(-10; -2)
22. А(4; -4) В(6; -10) С(10; 14)
23. А(6; -9) В(9; -6) С(-6; 30)
24. А(-4; 8) В(12; -4) С(0; 16)
25. А(2; 1) В(-1; 1) С(3; 2)
Завдання №9. Задано координати вершини піраміди. Знайти:
1. Рівняння грані .
2. Рівняння ребра .
3. Кут між ребром і гранню .
4.
Рівняння та довжину висоти
 ,
яка опущена з вершини
,
яка опущена з вершини
 на грань
.
на грань
.
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .
11. .
12. .
13. .
14. .
15. .
16. .
17. .
18. .
19. .
20. .
1. Рівняння грані .
2. Рівняння ребра .
3. Кут між ребром і гранню .
4. Рівняння та довжину висоти , яка опущена з вершини на грань .
Завдання №10.
Встановити, яка лінія задана даним рівнянням, та привести його до канонічного виду. Зробити малюнок.
1. х2+у2+10х-6у+25=0; 2. 4х2+у2+2х-14у+14=0;
3. 8х2+24х+12у+11=0; 4. 9х2-16у2-18х+32у+137=0;
5. у2+2х-10у+31=0; 6. 16х2+4у2+64х+8у+4=0;
7. 25х2+4у2-50х+24у+111=0; 8. у2-8х+4у+12=0;
9. -16х2+25у2+128х+50у-631=0; 10. 4х2+4у2+64х-4у+253=0;
11. 36х2-144у2-360х-1152у-6588=0; 12 .х2+6х-10у+19=0;
13. 9х2+9у2-12у-32=0; 14. 4х2+9у2-16х+36у+16=0;
15. 64х2-49у2+384х+490у+2487=0; 16. 45х2+45у2+30х-13=0;
17. 121х2+9у2-968х+36у+883=0; 18. у2+8х+12у+76=0;
19. 49х2-169у2-294х-2028у+2638=0; 20. х2+8х-5у+21=0;
21. 144х2-441у2+864х-62215=0; 22.144х2+49у2-288х-6912=0;
23. х2-4х-3у-2=0; 24. 16х2+121у2-96х-1792у=0;
25. 256х2-225у2-1800у-58500=0; 26. 4х2+81у2+810у+1701=0;
27. у2-3х-10у+31=0; 28. 2х2+2у2-2х+4у-7=0;
29. у2-5х-2у-14=0; 30. 289х2-225у2+1156х+900у+65281=0.
Питання для самоконтролю.
Поняття визначників другого та третього порядків.
Влавтивості визначників.
Методи обчислення визначників.
Що називається мінором та алгебраїчним доповненням визначника?
Матриці. Види матриць.
Операції над матрицями.
Обернена матриця. Алгоритм знаходження оберненої матриці.
Елементарні перетворення матриць.
Що називається рішенням СЛАР?
Рішення систем рівнянь за правилом Крамера.
Рішення СЛАР методом Гауса.
Рішення СЛАР за допомогою оберненої матриці.
Поняття вектора.
Скалярний, мішаний, векторний добутки векторів.
Види рівнянь прямої.
Парабола, її параметри, канонічне рівняння.
Гіпербола, її параметри, канонічне рівняння.
Еліпс, його параметри, канонічне рівняння.
