8.7. Свойства электропривода при настройке контура регулирования скорости на симметричный оптимум

Стандартная настройка контура регулирования скорости на технический оптимум широко используется на практике в связи с простотой технической реализации и благоприятным для большинства электроприводов характером протекания переходных процессов. Однако, как было установлено, точность регулирования при малом моменте инерции электропривода может быть ниже, чем в разомкнутой системе электропривода, и не удовлетворять предъявляемым требованиям. В этих случаях в многоконтурных унифицированных структурах регулирования координат электропривода прибегают к увеличению порядка астатизма системы по отношению к воздействию нагрузки.

Одним из возможных путей увеличения точности регулирования скорости при изменениях нагрузки является дополнение двухконтурной системы регулирования скорости, настроенной на технический оптимум, вторым контуром регулирования скорости, настроенным так же, как и первый.

Структурная схема трехконтурной системы с двумя контурами регулирования скорости и подчиненным контуром регулирования момента приведена на рис.8.19,а. Для внешнего контура регулирования скорости объектом регулирования является замкнутый внутренний контур, передаточная функция которого имеет вид

В результате последовательной коррекции необходимо получить следующую передаточную функцию разомкнутого внешнего контура регулирования скорости:

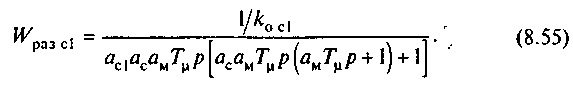
Следовательно, регулятор скорости внешнего контура регулирования должен иметь передаточную функцию интегрирующего звена

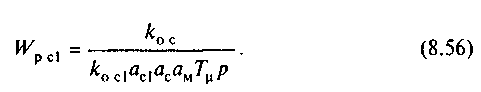
Передаточная функция замкнутой трехконтурной системы при настройке на технический оптимум (а_с1=а_с=а_м=2)

С помощью структурной схемы на рис.8.19,а, приняв k_oс1=k_0c, с учетом (8 39) и (8 56) получим выражение динамической жесткости механической характеристики

А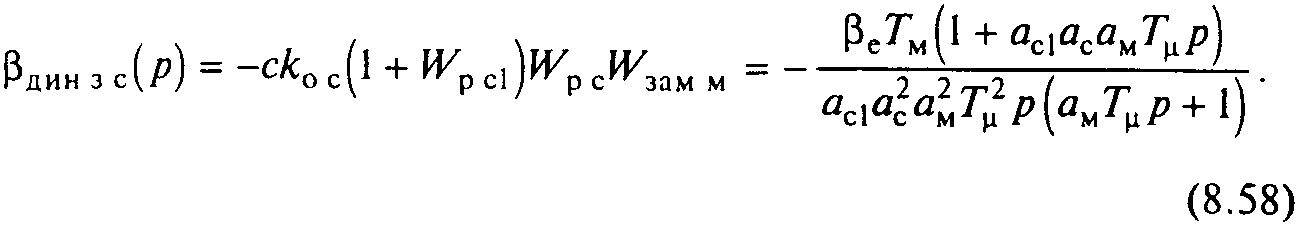 симптотическая ЛАЧХ динамической жесткости, соответствующая (8.58), для настройки на технический оптимум a_с1=а_с=а_м=2 представлена на рис.8.19,б. Сопоставление этой характеристики с аналогичной характеристикой двухконтурной системы (см. рис.8.14) свидетельствует о том, что введение дополнительного контура регулирования скорости обеспечивает астатическое регулирование скорости в области низких частот. В области сре-днечастотной асимптоты модуль динамической жесткости остается таким же, как и в двухконтурной системе, что дает основание предполагать, что при быстрых изменениях нагрузки точность регулирования в астатической системе незначительно отличается от динамической точности более простой двухконтурной системы.

Ошибку регулирования по управляющему воздействию определим с помощью передаточной функции разомкнутого контура (8.55):

Т рехконтурная система, как и двухконтурная, обладает аста-тизмом первого порядка по управляющему воздействию, причем динамическая ошибка при линейном нарастании задающего сигнала _0зс=₃/p составит

т . е. при добавлении третьего контура увеличивается в 2 раза по сравнению с (8.49). Так наглядно подтверждается отмеченная выше особенность многоконтурных систем подчиненного регулирования - при настройке на технический оптимум некомпенсируемая постоянная возрастает в 2^i-1 раз с возрастанием номеpa контура i. Соответственно возрастает и динамическая ошибка регулирования.

При настройке на технический оптимум a_c1=a_с=a_м=2

Д ля определения ошибки регулирования по возмущающему воздействию структурную схему на рис.8.19,a необходимо преобразовать. Сначала объединим две обратные связи по скорости в одну и используем упрощенную передаточную функцию замкнутого контура момента (рис.8.20,a). Затем перейдем к единичной обратной связи по скорости (рис 8.20,б) и получим удобную для поставленной цели структурную схему (рис.8.20,в). В соответствии с этой схемой и с учетом (8.58) можно записать

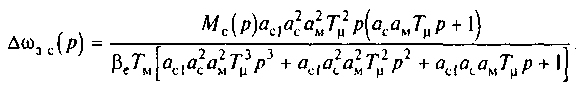
Как уже было отмечено, трехконтурная система обеспечивает астатическое регулирование и по нагрузке. Установившаяся ошибка при линейном нарастании нагрузки во времени ограничена значением

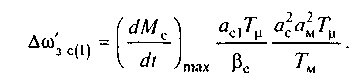
Таким образом, точность регулирования скорости в статических режимах в трехконтурной системе по сигналу задания сохраняется на том же уровне, что и в двухконтурной системе, а по нагрузке существенно возрастает, так как обеспечивается астатическое регулирование. В установившихся режимах линейного изменения задания ошибка регулирования больше в трехконтурной системе. Поскольку среднечастотная асимптота ЛАЧХ динамической жесткости в обеих системах одинакова, динамическая точность этих систем примерно одинакова. Характер переходных процессов при изменениях задающего сигнала соответствует настройке на технический оптимум, но быстродействие получается примерно в 2 раза ниже, чем в простейшей двухконтурной системе.

Обеспечить астатизм по нагрузке при регулировании скорости можно без применения второго контура регулирования скорости путем настройки двухконтурной системы на симметричный оптимум. Для реализации этого пути при последовательной коррекции контура регулирования скорости задаются желаемой передаточной функцией разомкнутого контура в виде (6.54), причем в связи с наличием подчиненного контура регулирования момента принимают Т_с=2Т:

Передаточная функция объекта регулирования при отбрасывании члена второго порядка в передаточной функции замкнутого контура момента имеет вид

Передаточная функция регулятора скорости

Получены передаточная функция ПИ-регулятора скорости и соотношения для расчета его параметров:

Передаточная функция замкнутого контура регулирования скорости по управлению

Для анализа реакции синтезированной системы на изменения нагрузки преобразуем полученную в результате коррекции структурную схему (рис.8.21,а) к виду, представленному на рис.8.21,б. Рассматривая последнюю структуру, можем записать передаточную функцию динамической жесткости механической характеристики замкнутой системы:

Ч астотная характеристика динамической жесткости представлена на рис. 8.22,а. Если сравнить рис.8.22,а с рис.8.19,б, можно убедиться в их полном совпадении, что свидетельствует об одинаковой точности регулирования скорости при изменениях нагрузки как в трехконтурной, так и в двухконтурной астатических системах.

Однако точность при отработке сигнала задания выше в двухконтурной системе, настроенной на симметричный оптимум. В соответствии с (8.62) и ЛАЧХ разомкнутого контура, показанной на рис.8.22,б, двухконтурная система с ПИ-регулятором скорости обладает астатизмом второго порядка. Изображение ошибки регулирования при изменениях управляющего воздействия в такой системе определяется с помощью (8.62):

Уравнение (8.65) показывает, что благодаря астатизму второго порядка установившаяся динамическая ошибка в режимах линейного нарастания задания ₀=₃t отсутствует. По этой причине двухконтурную систему с ПИ-регулятором скорости называют двукратноинтегрирующей системой и применяют в тех случаях, когда важно иметь высокую точность отработки изменений сигналов задания.

Наличие в ЛАЧХ разомкнутого контура (рис.8.22,б) низкочастотной асимптоты с наклоном -40 дБ/дек приводит к снижению запаса по фазе на частоте среза =1/4T по сравнению с настройкой на технический оптимум, что определяет значительно большие перерегулирования по скорости при отработке скачка задания, чем в трехконтурной системе.

Установившаяся ошибка при настройке на симметричный оптимум в режимах линейного нарастания задания ₃=₃t, как отмечено, равна нулю. Однако в начале процесса в связи с электромагнитной инерцией (8.65) определяет отставание изменения скорости от заданных значений _э (рис.8.23). Возникшая на этом этапе ошибка отрабатывается в течение времени t_p10·T_ с перерегулированием по моменту М и ускорению =d/dt, достигающим 56% установившихся значений М_уст=J_·_з (M_c=0) и _уст=_з.

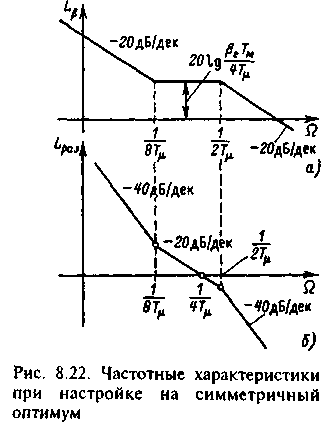
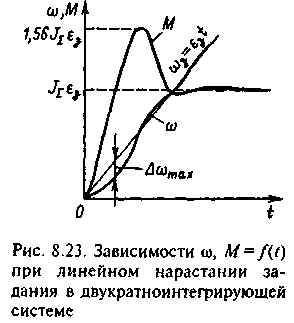
Поэтому в случаях, когда важно повысить жесткость механической характеристики и увеличить статическую точность регулирования при изменениях нагрузки, либо применяют рассмотренную выше трехконтурную структуру, либо корректируют реакцию двухконтурной системы на изменения управляющего воздействия путем введения на вход системы дополнительного звена. В частности, таким путем можно, не изменяя точности по нагрузке, получить настройку системы с ПИ-регулятором скорости по управлению, соответствующую техническому оптимуму. Сравнивая рис.8.20,в для трехконтурной системы с рис.8.21,в для системы с ПИ-регулятором скорости, можно убедиться, что для достижения этой цели необходимо на задающий вход регулятора включить фильтр с передаточной функцией

К этому же выводу можно прийти и путем сравнения передаточной функции замкнутой трехконтурной системы (8.57) с такой же передаточной функцией для настройки на симметричный оптимум в двухконтурной системе. При введении такого звена установившаяся ошибка при линейном нарастании задания уже получается не равной нулю, а определяется (8.60). Характер переходных процессов в системе при этом соответствует настройке на технический оптимум.