
- •1.2. Расчетные схемы механической части электропривода
- •1.3. Типовые статические нагрузки электропривода
- •1.4. Уравнения движения электропривода
- •1.5. Механическая часть электропривода как объект управления
- •1.6. Механические переходные процессы электропривода
- •1.7. Динамические нагрузки электропривода
- •1.8 Контрольные вопросы к гл. 1
- •Глава вторая Математическое описание динамических процессов электромеханического преобразования энергии
- •2.1. Общие сведения
- •2.2. Обобщенная электрическая машина.
- •2.3. Электромеханическая связь электропривода и ее характеристики
- •2.4. Линейные преобразования уравнений механической характеристики обобщенной машины
- •2.5. Фазные преобразования переменных
- •2.6. Структура и характеристики линеаризованного электромеханического преобразователя
- •2.7. Режимы преобразования энергии и ограничения, накладываемые на их протекание
- •2.8. Контрольные вопросы к гл. 2
- •Глава третья Электромеханические свойства двигателей
- •3.1. Общие сведения
- •3.2. Математическое описание процессов преобразования энергии в двигателе постоянного тока с независимым возбуждением
- •3.3. Естественные характеристики двигателя с независимым возбуждением
- •3.4. Искусственные статические характеристики и режимы работы двигателя с независимым возбуждением
- •3.5. Динамические свойства электромеханического преобразователя с независимым возбуждением
- •3.6. Математическое описание процессов электромеханического преобразования энергии в двигателе с последовательным возбуждением
- •3.7. Статические характеристики двигателя с последовательным возбуждением
- •3.8. Динамические свойства электромеханического преобразователя с последовательным возбуждением
- •3.9. Особенности статических характеристик двигателя со смешанным возбуждением
- •3.10. Математическое описание процессов электромеханического преобразования энергии в асинхронном двигателе
- •3.11. Статические характеристики асинхронных двигателей
- •3.12. Динамические свойства асинхронного электромеханического преобразователя при питании от источника напряжения
- •3.13. Статические характеристики и динамические свойства асинхронного электромеханического преобразователя при питании от источника тока
- •3.14. Режим динамического торможения асинхронного двигателя
- •3.15. Электромеханические свойства синхронных двигателей
- •3.16. Шаговый режим работы синхронного электромеханического преобразователя
- •3.17. Контрольные вопросы к гл. 3
- •Динамика обобщенной разомкнутой электромеханической системы
- •4.1. Общие сведения
- •4.2. Математическое описание и структурные схемы разомкнутых электромеханических систем
- •4.3. Обобщенная электромеханическая система с линеаризованной механической характеристикой
- •4.4. Динамические свойства электропривода с линейной механической характеристикой при жестких механических связях
- •4.5. Устойчивость статического режима работы электропривода
- •4.6. Понятие о демпфировании электроприводом упругих механических колебаний
- •4.7. Переходные процессы электропривода и методы их анализа
- •4.10. Переходные процессы электропривода с асинхронным короткозамкнутым двигателем
- •4.11. Динамика электропривода с синхронным двигателем
- •4.12. Особенности многодвигательного электропривода
- •4.13 Контрольные вопросы к гл. 4
- •Основы выбора мощности электропривода
- •5.1. Общие сведения
- •5.2. Потери энергии в установившихся режимах работы электропривода
- •5.3. Потери энергии в переходных процессах работы электропривода
- •5.4. Нагревание и охлаждение двигателей
- •5.5. Нагрузочные диаграммы электропривода
- •5.6. Номинальные режимы работы двигателей
- •5.7. Методы эквивалентирования режимов работы двигателей по нагреву
- •5.8. Понятие о допустимой частоте включений асинхронных двигателей с короткозамкнутым ротором
- •5.9. Контрольные вопросы
- •Глава шестая Регулирование координат электропривода
- •6.1. Общие сведения
- •6.2. Основные показатели способов регулирования координат электропривода
- •6.3. Система генератор-двигатель
- •6.4. Система тиристорный преобразователь-двигатель
- •6.5. Система преобразователь частоты - асинхронный двигатель
- •6.6. Обобщенная система управляемый преобразователь-двигатель
- •6.7. Связь показателей регулирования с лачх разомкнутого контура регулирования
- •6.8. Стандартные настройки регулируемого электропривода
- •6. 9. Контрольные вопросы к гл.6
- •Регулирование момента (тока) электропривода
- •7.1. Общие сведения
- •7.2. Реостатное регулирование момента
- •7.3. Система источник тока – двигатель
- •7.4. Автоматическое регулирование момента в системе уп-д
- •7.5. Последовательная коррекция контура регулирования момента в системе уп – д
- •7.6. Особенности регулирования момента и тока в системе г-д
- •7.7. Частотное регулирование момента асинхронного электропривода
- •7.8. Влияние отрицательной связи по моменту (току) на динамику упругой электромеханической системы
- •7.9. Контрольные вопросы к гл. 7
- •Регулирование скорости электропривода
- •8.1. Общие сведения
- •8.2. Реостатное регулирование скорости
- •8.3. Схемы шунтирования якоря двигателя постоянного тока с независимым возбуждением
- •8.4. Схемы шунтирования якоря двигателя постоянного тока с последовательным возбуждением
- •8.5. Автоматическое регулирование скорости в системе уп-д
- •8.6. Свойства электропривода при настройке контура регулирования скорости на технический оптимум.
- •8.7. Свойства электропривода при настройке контура регулирования скорости на симметричный оптимум
- •8.8. Регулирование скорости двигателя постоянного тока с независимым возбуждением изменением магнитного потока
- •8.9. Способы регулирования скорости асинхронного электропривода
- •8.10. Особенности частотного регулирования скорости асинхронного электропривода
- •8.11. Принцип ориентирования по полю двигателя при частотном управлении
- •8.12. Каскадные схемы регулирования скорости асинхронного электропривода
- •8.13. Каскады с однозонным регулированием скорости
- •8.14. Оптимизация регулируемого электропривода с упругими связями по критерию минимума колебательности
- •8.15. Контрольные вопросы к гл. 8
- •Регулирование положения
- •9.1. Общие сведения
- •9.2. Точный останов электропривода
- •9.3. Автоматическое регулирование положения по отклонению
- •9.4. Понятие о следящем электроприводе
- •9.5. Контрольные вопросы к гл. 9
- •Основы выбора системы электропривода
- •10.1. Общие сведения
- •10.2. Энергетическая эффективность электропривода
- •10.3 Особенности энергетики вентильных электроприводов
- •10.4. Надежность регулируемого электропривода
- •10.5. Контрольные вопросы к гл. 10
8.6. Свойства электропривода при настройке контура регулирования скорости на технический оптимум.
П оследовательная
коррекция контура регулирования скорости
позволяет создавать унифицированные
регулируемые электроприводы с
определенными стандартными показателями
Так как обычно наряду с необходимостью
регулирования скорости требуется
регулирование и момента (тока) двигателя,
рассмотрим физические свойства системы
УП-Д, в которой при регулировании скорости
работает подчиненный контур
регулирования
момента, оптимизированный методом
последовательной коррекции в §7.5. С
учетом передаточной функции замкнутого
контура регулирования момента (7.40)
структурная схема контура регулирования
скорости в обобщенной системе УП-Д
представлена на рис.8.13,а. В соответствии
с ней объект регулирования скорости
состоит из замкнутого контура регулирования
момента и механического звена
электропривода и имеет следующую
передаточную функцию:
оследовательная
коррекция контура регулирования скорости
позволяет создавать унифицированные
регулируемые электроприводы с
определенными стандартными показателями
Так как обычно наряду с необходимостью
регулирования скорости требуется
регулирование и момента (тока) двигателя,
рассмотрим физические свойства системы
УП-Д, в которой при регулировании скорости
работает подчиненный контур
регулирования
момента, оптимизированный методом
последовательной коррекции в §7.5. С
учетом передаточной функции замкнутого
контура регулирования момента (7.40)
структурная схема контура регулирования
скорости в обобщенной системе УП-Д
представлена на рис.8.13,а. В соответствии
с ней объект регулирования скорости
состоит из замкнутого контура регулирования
момента и механического звена
электропривода и имеет следующую
передаточную функцию:
![]()
Следуя рекомендациям, данным в §6.8, пренебрежем в передаточной функции Wзам.м членом, содержащим р2:
![]()
Соотношение (8 37) показывает, что для контура скорости некомпенсируемая постоянная времени Tc=амТ, т.е. в ам раз больше, чем для подчиненного контура регулирования момента. Желаемая передаточная функция для контура регулирования скорости
![]()
где ас=TОС/TС - соотношение постоянных контура скорости. Передаточная функция регулятора скорости
![]()
Необходим П-регулятор скорости с коэффициентом kpc. Так как выходное напряжение регулятора скорости является сигналом задания момента uзм для подчиненного контура, необходимо ограничить максимальное значение uзм, исходя из требуемого стопорного момента:
![]()
Характеристика UBЫX=f(UBX) регулятора скорости, отвечающая этому условию, представлена на рис.8.13,б. Передаточная функция замкнутого контура регулирования скорости
![]()
Выбором соотношения постоянных времени контура в пределах ас=24 можно получить требуемое по техническим условиям демпфирование колебаний скорости в переходных процессах и ограничить перерегулирование допустимым значением. Наиболее широко на практике используется стандартная настройка на технический оптимум ас=ам=2, при этом
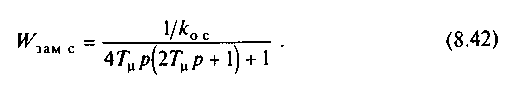
Рассмотрим, какими свойствами обладает электропривод при такой настройке контура регулирования скорости. Благодаря малости некомпенсируемой постоянной времени Т подчиненный контур регулирования момента обеспечивает в области малых и средних частот высокую точность регулирования момента, при которой допустимо пренебречь влиянием электромеханической связи и получить уравнение механической характеристики с помощью структурной схемы на рис.8.13,а при ам=2:
![]()
С помощью (8.39) уравнение (8.43) можно представить в виде
![]()
где
![]() Уравнение
статической механической характеристики
(р=0)
Уравнение
статической механической характеристики
(р=0)
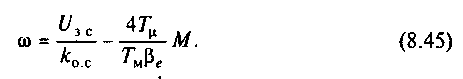
Это уравнение справедливо в пределах линейной части характеристики регулятора скорости, т. е. при (uзс-kос)/kрсUзмmax. При снижении скорости до значения гр=0зс-МСТОП/3с выходное напряжение регулятора скорости достигает максимального значения и при <гр М=Мстоп=const. Механические характеристики электропривода при настройке контура регулирования скорости и подчиненного контура регулирования момента на модульный оптимум показаны для различных Тм на рис.8.13,в.
В соответствии с (8.44) модуль жесткости механической характеристики в замкнутой по скорости системе определяется соотношением динамических параметров - постоянных времени ТМ и Т . Это объясняется выбором коэффициента обратной связи по скорости из условия получения определенных динамических показателей, соответствующих техническому оптимуму. Как следствие, точность регулирования при различных параметрах механической части оказывается существенно различной.
Если электропривод обладает большой механической инерцией и его электромеханическая постоянная Тм>4T, модуль жесткости механической характеристики в замкнутой системе зс выше, чем в разомкнутой е. При Тм=4T модуль жесткости в замкнутой системе остается тем же, что и в разомкнутой системе (зс=е). Для мощных приводов с малым приведенным моментом инерции (Тм<4T) жесткость механической характеристики в замкнутой системе получается меньшей, чем в разомкнутой системе (зс<е).
С труктурная
схема электропривода, соответствующая
(8.44), представлена на рис.8.14,а. Определим
с ее помощью передаточную функцию
динамической жесткости механической
характеристики в замкнутой системе:
труктурная
схема электропривода, соответствующая
(8.44), представлена на рис.8.14,а. Определим
с ее помощью передаточную функцию
динамической жесткости механической
характеристики в замкнутой системе:
![]()
Соответствующие (8.46) ЛАЧХ при различных отношениях ТМ/4Т приведены на рис.8.14,б. Там же для сравнения приведена ЛАЧХ динамической жесткости характеристики разомкнутой системы (штриховая прямая 1). Сравнивая их, можно заключить, что при Тэ>2Т область частот, в которой расхождения между статикой и динамикой невелики, расширяется и точность регулирования также зависит от отношения ТМ/4Т как и в статике.
В соответствии с (8.38) и схемой на рис.8.14,a изображение ошибки регулирования по управляющему воздействию при ам=ас=2 имеет вид

Положив в (8.47) р=0, можно убедиться, что при 0зс=const статическая ошибка по управляющему воздействию отсутствует, электропривод по управлению обладает астатизмом первого порядка.
Если управляющее воздействие нарастает по линейному закону
![]()
то в установившемся режиме будет иметь место постоянная ошибка, определяемая (8.47) при подстановке в эту формулу (8.48) и р=0:
![]()
Определим с помощью рис.8.14,a и формулы (6.19) изображение ошибки по возмущению, обусловленному статической нагрузкой электропривода Мс(р):

При р=0 и Мc=const (8.50) определяет статическую ошибку по нагрузке
![]()
которая определяется модулем жесткости механических характеристик в замкнутой системе электропривода (см. рис.8.13,в).
В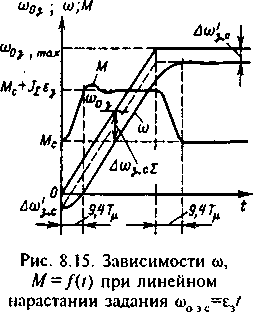 переходных процессах, обусловленных
изменениями задания по линейному закону
(8.43), установившаяся динамическая ошибка
(8.49) суммируется со статической (8.51):
переходных процессах, обусловленных
изменениями задания по линейному закону
(8.43), установившаяся динамическая ошибка
(8.49) суммируется со статической (8.51):
![]()
С учетом известного характера изменения переменных в переходных процессах при настройке на технический оптимум (8.48) и (8.52) позволяют установить вид зависимостей (t) и М(t) при линейном нарастании задающего сигнала и Мнач=Мс (рис.8.15). Так как перерегулирование и колебательность при aс=ам=2 пренебрежимо малы, максимум переходной ошибки на р.8.15 незначительно отличается от установившейся динамической ошибки зс.
Д ля
многих электроприводов по технологическим
условиям необходимо иметь минимальные
динамические падения скорости 'зс
в переходных процессах ударного
приложения нагрузки. Примерный вид
характеристики ,
M=f(t)
при настройке контура скорости на
технический оптимум при приложении
скачком момента Мс
показан на рис.8.16,я. По этим характеристикам
на рис.8.16,б построена характеристика
2, которая значительно отличается от
статической характеристики 1 в начале
процесса и быстро приближается к ней в
конце. В связи с малым перерегулированием,
свойственным настройке на технический
оптимум, максимум динамической ошибки
3с
определяется в своей основной части
статической ошибкой '3с,
определяемой жесткостью статической
характеристики.
ля
многих электроприводов по технологическим
условиям необходимо иметь минимальные
динамические падения скорости 'зс
в переходных процессах ударного
приложения нагрузки. Примерный вид
характеристики ,
M=f(t)
при настройке контура скорости на
технический оптимум при приложении
скачком момента Мс
показан на рис.8.16,я. По этим характеристикам
на рис.8.16,б построена характеристика
2, которая значительно отличается от
статической характеристики 1 в начале
процесса и быстро приближается к ней в
конце. В связи с малым перерегулированием,
свойственным настройке на технический
оптимум, максимум динамической ошибки
3с
определяется в своей основной части
статической ошибкой '3с,
определяемой жесткостью статической
характеристики.
Если важно минимизировать динамическое падение скорости и допустимо увеличить колебательность электропривода, на практике отступают от настройки на технический оптимум и выбирают при аM=2ас<2, при этом (8.51) можно представить так:
![]()
В соответствии с (8.53) при ас<2 возрастает модуль жесткости статической механической характеристики зс и уменьшается статическая ошибка '3с. Увеличение статической точности регулирования может в определенных пределах быть более существенным, чем возрастание динамических ошибок в связи с повышением колебательности электропривода. В этом можно убедиться, рассматривая рис.8.17, на котором построены для aм=2 зависимости зс* =f() при ас=2 (рис.8.17,а) и ас=1 (рис.8.17,б), причем
![]()

В качестве базового значения ошибки принята статическая ошибка '3c при аM=2, ас=2.
