7.5. Последовательная коррекция контура регулирования момента в системе уп – д

Для последовательной коррекции на вход разомкнутого контура регулирования момента в схеме на рис.7.9 введем регулятор момента с передаточной функцией W_рм, как показано на рис.7.14,а.

Условия последовательной коррекции существенно зависят от инерционности преобразователя. Имея в виду вентильные преобразователи напряжения и частоты для электроприводов постоянного и переменного тока, примем, что постоянная времени Т_п является оценкой постоянного запаздывания _п и инерционности фильтров T_ф, причем благодаря малости _n и Т_ф их можно отнести к некомпенсируемым инерционностям контура:

Как было показано, при регулировании момента электромеханическая связь, обусловленная внутренней связью по ЭДС, является возмущающим воздействием, снижающим точность регулирования. При последовательной коррекции выбором желаемой передаточной функции разомкнутого контура регулирования в виде (6.34) статическая ошибка регулирования момента исключается. Поэтому при синтезе контура регулирования момента внутреннюю обратную связь по скорости размыкают, пренебрегая ее влиянием на динамику привода в процессах по управлению. Влияние этой связи на динамическую точность регулирования можно оценить, положив изменения скорости независимым возмущающим воздействием =/(г).

Изложенному соответствует упрощенная структурная схема контура регулирования момента, представленная на рис.7.14,б. Запишем желаемую передаточную функцию разомкнутого контура (6.34) с учетом неединичной обратной связи в виде

В соответствии с рис.7.14,б передаточная функция объекта регулирования

Поделив (7 35) на (7.36), получим

Таким образом, регулятор момента должен быть пропорционально-интегральным (ПИ-регулятор) с постоянной интегрирования

и коэффициентом пропорциональной части

Передаточная функция замкнутого контура регулирования момента

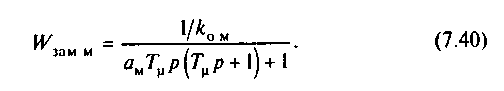
Исследуем свойства полученной системы электропривода. Уравнение механической характеристики получим на основании физических представлений. Благодаря наличию в передаточной функции регулятора момента (7.37) интегральной составляющей в статических режимах (U_{3 м}=const, p=0) на входе регулятора напряжение должно быть равно нулю:

Отсюда уравнение механической характеристики

Механические характеристики, соответствующие различным значениям U_3M, представлены на рис.7.15, причем при их построении учтено ограничение ЭДС или частоты преобразователя (₀_0max, штриховые предельные характеристики разомкнутой системы). Таким образом, в результате последовательной коррекции в статических режимах электропривод приобретает свойства регулируемого источника момента.

Д инамические свойства контура определяются в соответствии с (7.40) его настройкой, т. е. выбором соотношения постоянных времени контура а_м=Т_ОМ/Т. Контур момента чаще всего настраивается на технический оптимум (а_м=2), при котором минимальное время регулирования t=4,7T достигается при пренебрежимо малом перерегулировании, не превышающем 5%·M₃. Если по тем или иным причинам желательно полностью исключить перерегулирование или, напротив, допустимо увеличение колебательности для достижения, высокого быстродействия, значения а_м выбираются в пределах а_M=14.

При данном соотношении постоянных а_м быстродействие контура регулирования момента определяется уровнем некомпенсируемой постоянной Т. Для вентильных преобразователей T0,01 с и момент при скачке задания достигает заданного значения за время t_P<0,05с. Это высокое быстродействие, которое достаточно для большинства регулируемых электроприводов. Во многих случаях такой темп нарастания момента оказывается нежелательным или недопустимым по условиям работы механизма, тогда приходится принимать меры для его ограничения.

Одним из возможных путей ограничения производной момента является увеличение некомпенсируемой постоянной времени контура путем отказа от компенсации, например Т_э. Однако при этом следует учитывать, что увеличение Т приводит к увеличению ошибок регулирования в динамических процессах.

Для анализа точности регулирования момента воспользуемся общей формулой ошибки регулирования (7.19). С учетом схемы на рис.7.14,б при единичной обратной связи получим

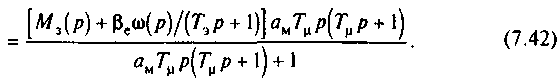
Рассматривая (7 42), можно заключить, что статическая ошибка регулирования момента как по управлению, так и по возмущению равна нулю. Установившаяся динамическая ошибка при линейном нарастании задания М₃(t)=(dM/dt)_maxt=(dMJdt)_max/p определяется по (7.42) при р=0:

Проанализируем влияние внутренней связи по скорости на точность регулирования момента в переходных процессах электропривода. Примем, что скорость двигателя изменяется по линейному закону (t)=_max·t=_max/p. Подставив изображение скорости в (7.42), при p=0 определим установившуюся динамическую ошибку по возмущению:

Таким образом, в переходных процессах вследствие влияния внутренней связи по скорости (электромеханической связи в разомкнутой системе электропривода) фактические значения момента в соответствии с (7.44) могут существенно отличаться от М₃, т. е. между динамическими и статическими характеристиками M=f(t) имеют место значительные расхождения. При данном ускорении _max эти расхождения тем больше, чем больше модуль жесткости статической характеристики электропривода в разомкнутой системе _e и чем выше уровень некомпенсируемых инерционностей контура регулирования, оцениваемый Т. Выбор повышенных значений а_м в целях снижения колебательности контура регулирования момента влечет за собой соответствующее увеличение ошибки регулирования момента в переходных процессах. Наличие ошибки (7.44) объясняется следующими причинами. Для поддержания момента постоянным М=const по мере возрастания скорости  должна линейно увеличиваться ₀, т. е. напряжение или частота на выходе преобразователя. Соответственно должно линейно возрастать выходное напряжение регулятора момента, а для этого на входе ПИ-регулятора должен быть постоянный сигнал ошибки U_вх=U_зм-k_омM.

Формулу, удобную для оценки динамической ошибки в переходных процессах пуска и торможения, можно получить, определив из уравнения движения ускорение _mах:

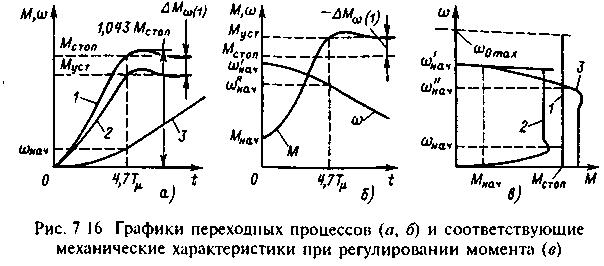
Подставив (7.45) в (7.44). после поеобоазований получим

где

Полученные соотношения и известные динамические показатели настройки на технический оптимум а=2 позволяют инженеру в практической деятельности производить оперативные качественные и количественные оценки переходных процессов в электроприводах с унифицированным контуром регулирования момента. При задании скачком момента М_з=М_стоп переходный процесс изменения момента при стандартной настройке определяется формулой (6.32) при а=2. Соответствующая зависимость M=f(t) представлена на рис.7.16,а (кривая 1). Она точно описывает переходный процесс при =0, т. е. при заторможенном роторе двигателя. Изменения скорости, обусловленные приложенным моментом в соответствии с уравнением движения

вызывают отличия реальной кривой 2 от теоретической 1 тем большие, чем больше динамические ошибки регулирования момента. Кривая 3 на рис.7.16,a характеризует нарастание скорости (t) в процессе пуска с М_с=0, соответствующее изменениям момента по кривой 2. Нетрудно видеть, что после начального переходного процесса скорость при пуске с М_с=const изменяется по линейному закону =_нач+_maxt, при этом устанавливается постоянная ошибка М_(1), которая вычисляется по (7.46).

Характер изменения момента на начальном участке кривой 2 может несколько отличаться от кривой 1, соответствующей =0. Однако эти отличия незначительны и существенного влияния на общий характер и время переходного процесса не оказывают. Поэтому кривая 2 приближенно может быть построена по установившемуся значению М_п=М_стоп-М_(1) при t14,7T аналогично построению кривой 1.

На рис.7.16,б приведены такие же кривые для процесса сто-порения электропривода, вызванного приложением момента нагрузки М>M_стоп. За время нарастания момента от М_нач до М_уст=M_стоп+M_(1) t14,7T скорость успевает снизиться от '_нач до ''_нач и далее уменьшается по линейному закону =''_нач-_maxt. В соответствии с (7.46) при стопорении под действием М_с>М_сmоп ошибка М_(1) отрицательна и значение М_уст>М_стоп.

На рис.7.16,в представлены статическая характеристика 1 и соответствующие пуску (рис.7.16,о) и стопорению (рис.7.16,б) динамические механические характеристики 2 и 3. Они наглядно показывают расхождения между статикой и динамикой регулирования момента. Во многих случаях эти расхождения при стандартных настройках оказываются недопустимо большими и возникает необходимость введения в контур регулирования момента дополнительных узлов, повышающих точность регулирования.