6.8. Стандартные настройки регулируемого электропривода

При последовательной коррекции структурная схема контура регулирования переменной х может быть представлена, как показано на рис.6.16, состоящей из регулятора с передаточной функцией W_{p x} и объекта регулирования с передаточной функцией W_opx. Передаточная функция разомкнутого контура

Примем, что передаточная функция объекта регулирования имеет вид

где _п - постоянное запаздывание; T_i - постоянные времени элементов объекта регулирования, расположенные в порядке убывания по значению.

Предположим, что передаточная функция регулятора реализована в виде

где  - число больших и средних постоянных времени. Тогда передаточная функция разомкнутого контура

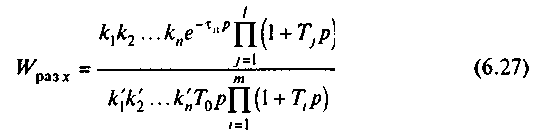
Полученное выражение свидетельствует о том, что формированием передаточной функции регулятора можно направленно видоизменять передаточную функцию разомкнутого контура. Действительно, при k₁=k'₁, k₂=k'₂,..., k_n=k'_n и T_j=T_i исходная передаточная функция существенно видоизменяется:

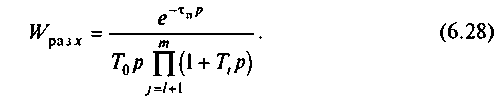
В ней введением регулятора с передаточной функцией (6.26) и подбором его параметров исключено  инерционных звеньев, обладающих большими и средними T_i, сокращено п частных коэффициентов и введено интегрирующее звено.

Исключение из передаточной функции разомкнутого контура звеньев с большими и средними постоянными времени открывает возможности повышения быстродействия контура регулирования. Эта операция реальные физические инерционные звенья из контура, разумеется, не исключает Однако их действие, замедляющее протекание переходных процессов, компенсируется действием соответствующих форсирующих звеньев, содержащихся в регуляторе, ускоряющих в требуемой степени реакцию системы.

В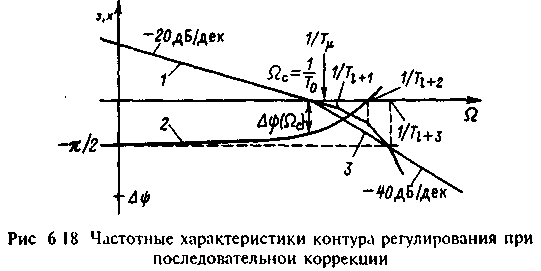 ведение интегрирующего звена, которое в W_op отсутствовало, обеспечивает повышение точности регулирования, так как контур приобретает астатизм первого порядка (v=1). Положительным изменением является и исключение частных коэффициентов k₁, k₂, ..., k_n контура регулирования, благодаря которому все показатели регулирования определяются обобщенным фактором - соотношением постоянных времени инерционных элементов контура.

Пытаться компенсировать весьма малые постоянные времени звеньев контура нецелесообразно, так как технические трудности компенсации быстро возрастают при уменьшении значений постоянных времени, а влияние на быстродействие привода соответственно убывает. Особые трудности представляет компенсация дискретности и малого запаздывания _п ряда быстродействующих преобразователей. Как следствие, в (6.28) остались некомпенсированными несколько (m-) малых постоянных T_i и постоянная _п. Достоинством (6.28) является возможность выбора требуемого значения постоянной Т₀. Этот выбор и определяет настройку контура регулирования. Если выбрать Т₀ из условия T₀>T_i+1 где T_i+1, как было принято, является наибольшей из оставшихся некомпенсированными постоянных T_i, то можно представить частотные характеристики (6.28), как показано на рис.6.18 Низко- и среднечастотная асимптота ЛАЧХ имеет наклон -20 дБ/дек (прямая 1), а запас по фазе на частоте среза (_c), определяемый по кривой 2, зависит от степени удаленности частоты среза 1/T₀ от ближайшей частоты сопряжения 1/Т_i+1. С учетом постоянной запаздывания _п, влияние которой в кривой 2 проявляется, запас по фазе на частоте среза составит:

Углы _c в (6.29) невелики, так как на соответствующих частотах сопряжения arctgT_i_i=arctg 1=/4. Так как Т₀>Т_i+1, arctg T_i_c</4 и приближенно можно принять arctgT_iQ_CТ_i_с.

Следовательно,

где - суммарная некомпенсированная постоянная контура регулирования, эквивалентная по потере запаса по фазе на частоте среза всем его реальным некомпенсированным инерционностям.

С учетом (6.30) передаточную функцию (6.28) можно с достаточной точностью представить в виде

Соответствующая (6.31) ЛАЧХ контура регулирования в области низких и средних частот совпадает с прямой 1 (рис.6.18), а в области высоких частот представляется асимптотой 3, имеющей наклон -40 дБ/дек. Частота сопряжения для этой асимптоты 1/T_ расположена ближе к частоте среза, чем и учитывается определяемое (6.29) влияние всех малых постоянных на динамические свойства контура регулирования.

Таким образом, доказано, что при выполнении определенных условий свойства контура регулирования с приемлемой для инженерной практики точностью при последовательной коррекции определяются передаточной функцией (6.31), имеющей второй порядок.

При этом передаточная функция замкнутого контура регулирования будет иметь вид

а корни характеристического уравнения равны:

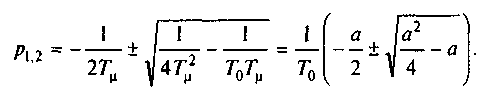
где а=T₀/T_ - соотношение постоянных контура регулирования. При а<4 движение электропривода в переходном процессе при скачке задания и нулевых начальных условиях определяется следующим уравнением:

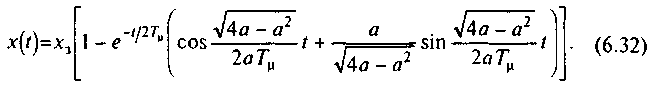
Суммарная некомпенсируемая постоянная T полностью определяет быстродействие электропривода по показателю общего времени переходного процесса t_пп. В соответствии с (6.32) свободные составляющие переходного процесса затухают в течение времени

Колебательность электропривода аналогично разомкнутой линеаризованной системе определяется соотношением постоянных контура а; этот же показатель определяет перерегулирование. Следовательно, подбором соотношения постоянных а можно обеспечить требуемые динамические показатели при быстродействии, ограниченном уровнем суммарной некомпенсированной постоянной времени Т_.

Изложенное составляет основу широко используемого в практике электропривода инженерного метода синтеза контуров регулирования координат электропривода. Задавшись требуемым соотношением постоянных а и определив по (6.30) Т , можно записать желаемую передаточную функцию разомкнутого контура:

передаточная функция объекта регулирования имеет вид:

Передаточная функция регулятора в соответствии с (6.24) определяется так:

Рассматривая (6.36), можно убедиться, что передаточная функция регулятора по мере увеличения числа компенсируемых постоянных  усложняется. При =0 (все T_i малы) она принимает вид

где T_и=(k,k₂...k_n)aT.

В этом случае регулятор представляет собой интегратор с постоянной интегрирования Т_и (И-регулятор). При =1

т е. требуется пропорционально-интегральный регулятор (ПИ-регулятор). При =2 необходим пропорциональный интсгро-дифференциальный регулятор (ПИД-регулятор) и с дальнейшим увеличением  в его передаточной функции требуется двухкратное и большей кратности дифференцирование входного сигнала. Исходя из требования необходимой помехозащищенности контура, допускают лишь однократное дифференцирование сигнала, т. е. компенсируют не больше двух больших и средних постоянных времени. Если в контуре регулирования координаты х имеется больше двух подлежащих компенсации больших и средних постоянных Т_i, прибегают к введению подчиненных контуров регулирования. Допустим, необходимо регулировать выходную переменную х₃ электропривода, структурная схема которого показана на рис.6.19, причем по условиям помехозащищенности желательно применять регуляторы не сложнее ПИ-регулятора. Эту задачу можно решить, если ввести вспомогательные контуры регулирования таким образом, чтобы в каждом контуре оказалась только одна из подлежащих компенсации постоянных Т₁Т_i.

В структуре на рис.6.19,а в контуре регулирования х₃ требуется, чтобы имелась компенсация трех больших и средних постоянных T₁, Т₂, Т₃ и регулятор W_px3(1) при одноконтурной системе в передаточной функции содержал бы дифференцирующую составляющую второго порядка В соответствии с (6.36) при этом

Рассмотрим, как повлияет на регулирование координаты х₃ введение двух вспомогательных контуров регулирования переменных х1 и х₂ (рис.6.19,б) Для этого вначале определим передаточную функцию регулятора внутреннего контура регулирования переменной x1 пользуясь изложенным методом.

Для первого контура желаемая передаточная функция

Передаточная функция объекта регулирования переменной x₁

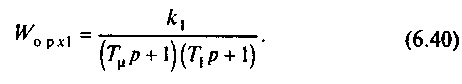
Определяем передаточную функцию регулятора:

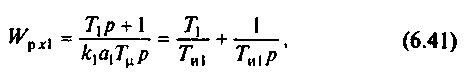
где T_и1=k₁a₁T

Как и требовалось, получен ПИ-регулятор. Передаточная функция замкнутого первого контура

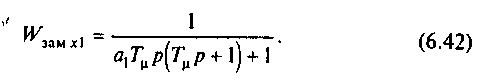
С учетом (6.42) передаточная функция объекта регулирования переменной х₂ принимает вид

Если выбрать a₁ таким образом, чтобы внутренний контур представлял собой высокодемпфированное звено, (6.43) можно существенно упростить. Выполненные расчеты и практика настройки регулируемых электроприводов показывают, что без большой погрешности для оценки качества регулирования в знаменателе (6.42) при переходе к (6.43) можно отбросить член второго порядка, при этом

Объект регулирования переменной х₂ наглядно представлен на рис.6.19,в. Здесь показано, что в результате введения первого контура из второго контура регулирования исключена большая постоянная T₁, а оценка некомпенсированных инерционностей второго контура принимает значение Т_2=а₁Т_. Соответственно желаемая передаточная функция для второго контура запишется в виде

передаточная функция регулятора х₂ получается путем деления (6.45) на (6.44):

где Т_н2=k₂a₂a₁T. Вновь получена передаточная функция ПИ-регулятора. Передаточная функция замкнутого второго контура

Выбором а₂ и здесь обеспечиваются свойства высокодемпфированного колебательного звена, что при переходе к регулированию основной координаты х₃ позволяет представить передаточную функцию объекта регулирования в упрощенном виде:

Структурная схема внешнего контура регулирования переменной х₃ при введении двух вспомогательных контуров регулирования, как показано на рис.6.19,г, претерпевает существенные изменения. Сравнивая рис.6.19,г с рис.6.19,a, можно установить, что в результате введения контуров регулирования х1 и х₂ на динамику внешнего контура в пределах линейности системы исключено влияние больших постоянных времени T1 и Т₂. Однако при этом изменилась суммарная некомпенсированная инерционность контура, оценка которой составляет T_3=а₂а₁Т. Желаемая передаточная функция при этом запишется в виде

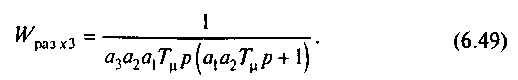
Передаточная функция регулятора х₃

где T_и3=k₃а₃а₂а₁T_ - постоянная времени ПИ-регулятора переменной x₃. При принимавшихся по мере решения задачи допущениях передаточная функция замкнутого внешнего контура регулирования приближенно соответствует колебательному звену второго порядка:

И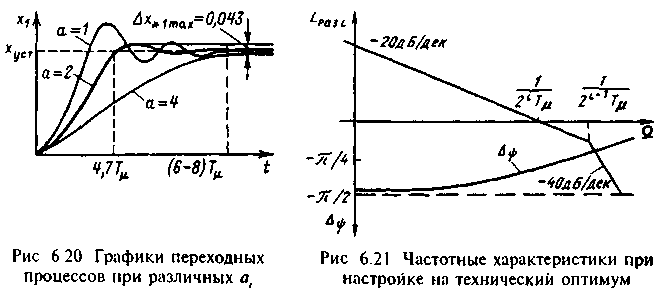 з изложенного следует, что введение вспомогательных контуров регулирования имеет целью формирование благоприятной для последовательной коррекции передаточной функции объекта регулирования (рис.6.19,г). Вспомогательные контуры называют подчиненными контурами регулирования, а структура на рис.6.19,б представляет собой структуру подчиненного регулирования координат электропривода. Динамические показатели качества регулирования каждой переменной определяются соотношением постоянных а₁. На рис.6.20 представлен ряд зависимостей x₁=f(t) при различных значениях a₁ Если а₁=4, переходный процесс имеет апериодический характер, а время регулирования t=t_пп=(68)Т. Уменьшение а1 до а1=2 явно увеличивает колебательность, появляется перерегулирование, при этом время регулирования уменьшается. Дальнейшее уменьшение а, влечет за собой быстрое возрастание колебательности и перерегулирования, а эффект уменьшения /р постепенно снижается. Кривая, соответствующая a1=2, на рис.6.20 выделена утолщенной линией. Это значение соотношения постоянных контура регулирования обеспечивает минимальное время регулирования t_р=4,7T_ при практически пренебрежимом перерегулировании x_1max*=0,043. Такая настройка оптимальна для множества электроприводов, поэтому используется в качестве основной стандартной настройки и называется настройкой на технический оптимум или оптимум по модулю.

При настройке всех контуров регулирования на технический оптимум (а_i=2) передаточную функцию i-го разомкнутого контура с помощью (6.45) и (6.49) можно записать так:

То же для замкнутого контура

Следовательно, при прингятых допущениях переходные процессы в i-м контуре при настройке на технический оптимум по характеру совпадают с представленным для а=2 на рис.6.20. Расчетами установлено, что в результате влияния отброшенных в (6.52) и (6.53) членов более высокого порядка при увеличении номера контура i несколько увеличивается перерегулирование и возрастает колебательность. Однако в большинстве случаев это влияние можно полагать пренебрежимо малым. Логарифмические частотные характеристики i-го контура, настроенного на технический оптимум, представлены на рис.6.21. Рассматривая ЛАЧХ, можно убедиться, что с увеличением номера контура i быстродействие уменьшается, так как возрастает некомпенсированная постоянная Т_i и уменьшается частота среза _Сi=1/2ⁱТ. Таковы общие характеристики стандартной настройки регулируемого электропривода на технический (модульный) оптимум. В случаях, когда требуется более высокая точность регулирования, при том же подходе применяют стандартную настройку на симметричный оптимум. При такой настройке желаемую передаточную функцию разомкнутого контура регулирования записывают в виде

Ф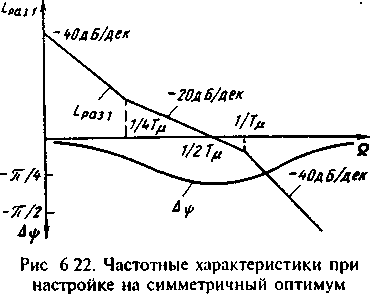 ормула (6.54) записана для первого контура и может быть применена для следующих контуров, если в нее подставлять соответствующие значения Т_i=2^i-1Т. Здесь, как и ранее, предполагается, что все некомпенсируемые инерционности исходного объекта Т заключены в первом, внутреннем контуре. Частотные характеристики, соответствующие (6.54), представлены на рис.6.22. Разомкнутый контур при этом обладает астатизмом второго порядка, что увеличивает точность регулирования, особенно в процессах, близких к статическим. Вместе с тем наличие протяженного участка в низкочастотной части с наклоном -40 дБ/дек уменьшает запас по фазе на частоте среза и увеличивает перерегулирование, которое может достигать 56%, что во многих случаях неприемлемо. Сравнивая рис.6.22 с рис.6.21, можно установить, что при средних и высоких частотах ЛАЧХ при настройках на технический и симметричный оптимум совпадают. Следовательно, быстродействие и затухание колебаний в системе при этих двух стандартных настройках примерно одинаковы.