4.6. Понятие о демпфировании электроприводом упругих механических колебаний

Представляя электропривод простейшей структурной схемой на рис.4.7, необходимо помнить, что неучет упругих механических связей всегда в той или иной степени искажает фактический характер процессов. Наряду с задачами, для решения которых в конкретных условиях эти искажения не имеют существенного значения, имеется широкий круг практических вопросов, правильно решить которые без учета упругостей .невозможно. Кроме того, при решении любых задач нужно уметь оценивать влияние упругих связей на динамику электромеханической системы. Поэтому анализ особенностей взаимодействия электропривода, обладающего линейной механической характеристикой, с механизмом, содержащим упругие связи, в единой системе имеет важное практическое значение.

Проведем анализ влияния упругих связей с помощью обобщенной структуры электромеханической системы, представленной на рис.4.5. Для удобства анализа процессов по управлению положим М_с1=М_с2=0 и воспользуемся преобразованной структурной схемой механической части, приведенной на рис.1.12,в. Полученная таким образом структурная схема электропривода с упругой связью приведена на рис.4.14. Здесь передаточные функции механической части выражены через обобщенные параметры , ₁₂ и Т_м1=J₁/, причем T_м1=J_ (см. §1.5).

Обращаясь к анализу свойств механической части, выполненному в §1.5, можно заключить, что в структуре на рис.4.14 механическая часть объекта представляет собой консервативное колебательное звено, в котором при М=const возникшие механические колебания при принятых допущениях не затухают. Однако, рассматривая схему на рис.4.14, можно установить, что колебания скорости двигателя со, благодаря наличию внутренней обратной связи по скорости в системе электропривода должны вызывать колебания момента, обусловленные динамической жесткостью механической характеристики:

При отсутствии электромагнитной инерции (T₁=0)

Сравнивая эту зависимость с (1.18), можно убедиться, что при отсутствии электромагнитной инерции двигатель создает воздействующий на первую массу момент, аналогичный моменту вязкого трения. Следовательно, электропривод благодаря наличию электромеханической связи оказывает на колебания в механической части демпфирующее действие, аналогичное действию вязкого трения. Степень затухания колебаний в консервативной механической системе является количественным показателем демпфирующей способности электропривода.

Рассмотрим эффект демпфирования упругих колебаний на простейшем примере, предположив, что момент инерции второй массы настолько велик, что она практически не совершает колебаний, а электромагнитная инерция настолько мала, что можно принять Т_э=0. Этим условиям соответствуют электромеханическая схема на рис.4.15,а и структурная схема, изображенная на рис.4.15,б. Путем преобразования этой структуры получим передаточную функцию объекта по управляющему воздействию ₀:

Характеристическое уравнение системы

Корни данного уравнения

Если ₂>1/2T_M1 корни являются комплексно-сопряженными:

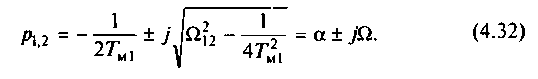
Нетрудно видеть, что при T_м колебания в рассматриваемой упругой электромеханической системе затухают вследствие демпфирующего действия электропривода. Рассмотрим влияние параметров электропривода на затухание колебаний, характеризуемое логарифмическим декрементом

Пусть якорь двигателя питается от источника тока I_я=I₁==const, тогда при Ф=Ф_ном=const M=сI₁=М₁=const. Механическая характеристика двигателя, соответствующая этому режиму, приведена на рис.4.16,a (прямая 1). Ей соответствуют =0 и T_m1=, при этом по (4.33) =0. Следовательно, при =0 демпфирующее действие электропривода на механические колебания отсутствует.

Подключив якорь к источнику регулируемого напряжения u_я, можно при различных u_я вводить добавочные резисторы R_доб с такими сопротивлениями, при которых I_кз=I₁=const, и получить семейство механических характеристик 2-7, показанных на рис.4.16,а. Этим характеристикам соответствуют значения

изменяющиеся в пределах от 0 до _е. При увеличении  от 0 до _е значения Т_м1 изменяются от  до T_м1е и в соответствии с (4.33) затухание колебаний постепенно увеличивается. При =_кр, когда 2T_м1кр₁₂=1, в соответствии с (4.33) =0о и переходный процесс в системе приобретает апериодический характер. Таким образом, зависимость =f() имеет вид, показанный на рис.4.16,б (кривая 1). Рассматривая эту кривую, можно убедиться, что изменение жесткости механической характеристики является эффективным средством изменения колебательности системы. Каждому значению J₁ и с₁₂ соответствует определенное значение _кр, обеспечивающее критическое демпфирование (=):

П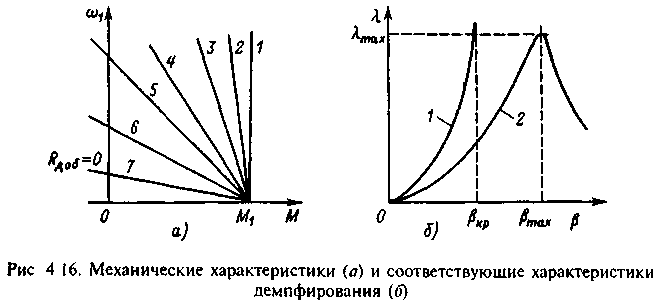 ри J₂= дальнейшее увеличение  в области >_кр в соответствии с (4.32) вызывает монотонное возрастание коэффициента затухания а, так как вторая масса колебаний совершать не может. При конечных значениях J₂ и  вторая масса вовлекается в процесс колебаний, причем в случае жесткой заделки первой массы возникшие колебания не затухают. Следовательно, если принять, что , и Т_M10, то в двухмассовой системе демпфирование должно уменьшаться и 0. Зависимость =f() для двухмассовой упругой электромеханической системы показана на рис.4.16,б (кривая 2). Здесь высокое демпфирование соответствует более узкой области значений р, причем существует оптимальное значение _mах, при котором =_1mах. Значения _mах зависят от конкретного сочетания параметров электромеханической системы, и при высоком демпфировании может существовать область значений , которым соответствуют =_mах=.

З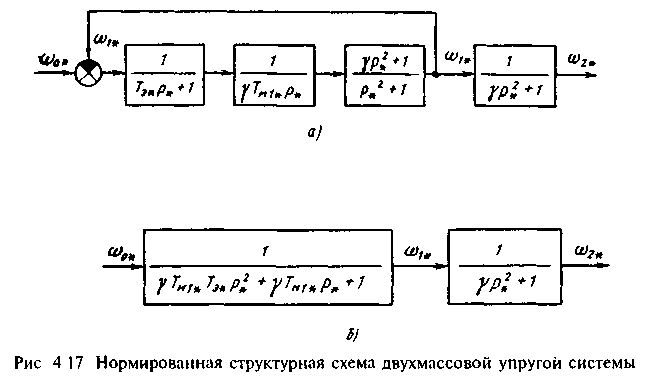 нание взаимосвязи демпфирующего действия электропривода с параметрами системы имеет важное практическое значение, при этом особый интерес представляет выявление сочетаний параметров, обеспечивающих возможный максимум демпфирования, т. е. значения _mах и их связь с параметрами системы. Анализ этих закономерностей упрощается удачным выбором системы обобщенных параметров и относительных единиц, через которые выражаются коэффициенты и переменные исходной структурной схемы электромеханической системы. Преобразованные таким образом структурные схемы называют нормированными структурными схемами.

Примером нормированной структурной схемы может служить схема на рис.4.14. Рассматривая ее, можно убедиться, что все частные коэффициенты в исходном математическом описании выражены через минимальное число обобщенных параметров: , ₁₂, Т_м1, Т_э. Число этих параметров можно сократить еще на единицу, использовав переход к относительному безразмерному времени t_*=₁₂t и соответственно к безразмерному оператору р_*=р/₁₂ Нормированная структура электромеханической системы при безразмерном времени t_* представлена на рис.4.17,а, причем T_М1*=T_м1₁₂ и T_э*=Т_э₁₂.

С помощью общего приема преобразования структурных схем определим по рис.4.17,a передаточную функцию системы по управлению при выходной величине _2*;

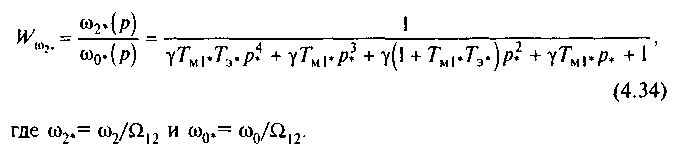
Характеристическое уравнение системы представим в виде

Корни (4.35) являются полюсами передаточной функции (4.34) и в связи с отсутствием в ней нулей полностью определяют вид частотных характеристик и переходных процессов по управлению _0*(p_*). В зависимости от сочетания параметров уравнение (4.35) может иметь либо две пары комплексно-сопряженных корней либo два комплексно-сопряженных и два действительных корня либо, наконец, все действительные корни. Прямой оценкой колебательности системы при этом может служить логарифмический декремент

где  и _p - показатель затухания и резонансная частота для той пары корней, которой соответствует меньшее значение .

Минимальное число обобщенных параметров, от которых зависят корни (4.35), создает благоприятные условия для обобщенного анализа демпфирующего действия электропривода в разомкнутой системе. При T_э*=const колебательность электромеханической системы в соответствии с (4.35) зависит только от соотношения масс  и от относительной электромеханической постоянной T_M1*=J₁₁₂/. Проведем анализ зависимости =f(; T_M1) Для случая Т_Э*=0. Подставляя это значение в (4.35), получаем

Примем, что имеется возможность изменять модуль жесткости механической характеристики в пределах от бесконечности до нуля, что обеспечит при данных параметрах механической части , ₁₂ и J₁ изменения постоянной времени T_м1, также от 0 до . Рассмотрим, какими свойствами будет обладать система при крайних значениях варьируемого параметра T_м1*. При T_M1*= (=0) уравнение (4.37) примет вид

т. е. при этом система содержит недемпфированное механическое колебательное звено с частотой свободных колебаний ₁₂.

Как выше было показано, при =0 электромеханическая связь отсутствует, момент М не колеблется, отвода энергии колебаний в электрическую часть системы нет, поэтому демпфирующее действие не проявляется.

При T_M1*=0 (=) уравнение (4.37) также упрощается:

Корни этого уравнения p_*1,2=±j/. Переходя к действительному времени t, получаем

где - частота свободных колебаний массы j₂ при жесткой заделке вала двигателя. В этом случае отсутствуют колебания массы двигателя J₁ и демпфирующая способность электропривода оказывается равной нулю по причине чрезмерно сильной электромеханической связи.

Таким образом, как при предельно слабой электромеханической связи (=0), так и при предельно сильной (жесткой) электромеханической связи (=) демпфирующий эффект отсутствует и логарифмический декремент (4.36) равен нулю. При увеличении  от нуля T_M1*=T_M1*₁₂ уменьшается, логарифмический декремент возрастает до максимума и при дальнейшем увеличении  вновь стремится к нулю, как это и показано на рис.4.16,б (кривая 2), где значению _mах соответствует оптимальное значение (Т_M1*)_max.

Из изложенного следует, что каждому значению  соответствует один максимум _mах, который наступает при определенном значении (Т_M1*)_max. Таким образом, _mях в системе без электромагнитной инерции зависит только от соотношения инерционных масс =J_/J₁. Оптимальная жесткость механической характеристики зависит от параметров механической части:

Формула (4.39) свидетельствует о том, что чем больше частота свободных механических колебаний системы, тем при большей жесткости _max достигается максимум логарифмического декремента _mах.

Определяющее влияние соотношения масс  на демпфирование колебаний, обусловленных упругими механическими связями, связано с отмеченной выше особенностью системы: создаваемый электроприводом момент вязкого трения воздействует непосредственно на первую массу упругой системы, поэтому отвод энергии колебаний от второй массы возможен только через упругое взаимодействие масс, реализующееся в моменте упругой связи М₁₂. Чем больше , т. е. чем больше момент инерции второй массы J₂, тем нагрузка упругой связи при колебаниях больше, тем больше вызываемые колебаниями М₁₂ колебания первой массы J₁ тем выше предельное демпфирование. При небольших моментах инерции второй массы (J₂<<J₁ 1), электромеханическая связь и демпфирование колебаний пренебрежимо малы.

В этом можно убедиться с помощью структурной схемы на рис.4.17,a. Если 1, передаточная функция ее части, охваченной отрицательной связью по скорости ₁ вырождается в колебательное звено, показатель колебательности которого m, как выше установлено, определяется соотношением постоянных времени Т_э* и T_M1* (рис.4.17,б), упругие колебания в движении первой массы не проявляются. При этом демпфирование колебаний второй массы отсутствует (если не учитывать естественного демпфирования за счет внутренних диссипативных сил), что следует иметь в виду при проектировании и наладке электроприводов.

Рассмотренное физическое свойство электропривода - его демпфирующее действие на упругие электромеханические колебания, возникающие в динамических режимах работы, относится к числу особо важных в практическом отношении. Еще недавно, до середины XX в., особенности взаимодействия электропривода с приводимым в движение механизмом, содержащим упругие механические связи, практически не привлекали внимания специалистов по электроприводу, а специалисты - механики проблемы борьбы с колебательными нагрузками механизмов, существенно снижающими их надежность работы и долговечность, решали, как правило, при простейшем представлении момента электропривода как независимой функции времени без учета демпфирующего действия электропривода. Создание уникальных по точности и производительности машин и технологических комплексов резко обострило эти проблемы.

Так, в процессе создания мощных шагающих экскаваторов машиностроители столкнулись с явлением возрастания динамических нагрузок резонансного характера в электроприводах поворота, вызывающих недопустимые вибрации и тряску при повороте экскаватора. Выполненные исследования показали, что неучет особенностей взаимодействия многодвигательного электропривода поворота с многомассовой упругой механической системой создавал условия, исключающие демпфирующее действие электропривода, что и приводило при наличии внутренних возмущений к опасным резонансным колебаниям, нелинейным вследствие наличия зазоров в передачах. Только принятие мер для реализации максимального демпфирования этих колебаний электроприводом позволило обеспечить работоспособность и высокую производительность машин.

Проведенные исследования динамики сложных электромеханических систем с упругими связями, зазорами и кинематическими погрешностями передач заложили основы нового важного интенсивно развивающегося раздела общей теории электропривода - теории упругих электромеханических систем. Главным содержанием этого раздела является анализ физических особенностей электромеханических систем в их многообразии, установление взаимосвязи структуры и параметров электропривода с колебательностью электромеханической системы, разработка методов синтеза электроприводов и оптимизации их режимов работы по критерию минимума колебательности. Так как современный электропривод, как правило, обеспечивает автоматическое регулирование координат по отклонению, возможности оптимизации динамики достаточно широки. Они будут кратко рассмотрены в гл.8 после изучения свойств регулируемого электропривода при стандартных настройках контуров регулирования момента и скорости.