4.5. Устойчивость статического режима работы электропривода

Статическому режиму работы соответствует движение всех элементов электромеханической системы с постоянной и одинаковой приведенной скоростью. Этот режим наступает после затухания свободных составляющих переходного процесса, вызванного изменением управляющего или возмущающих воздействий, и характеризуется равенством электромагнитного момента двигателя суммарному моменту нагрузки.

Последнее следует непосредственно из уравнений движения электропривода, если положить в них р=0. Так, для электромеханической системы с упругой связью, положив p=0 в (4.5), получим

откуда

Для одномассовой расчетной механической схемы, приняв р=0 в уравнении движения электропривода

получим тот же результат: М=М_с.

В гл.1 было показано, что в общем случае момент нагрузки в той или иной степени зависит от скорости. Зависимость M_c=f() или =f(М_с) является механической характеристикой исполнительного механизма, а так как момент двигателя также в соответствии с его механической характеристикой зависит от скорости, условие статического режима можно записать в таком виде:

где _с - скорость электропривода в статическом режиме.

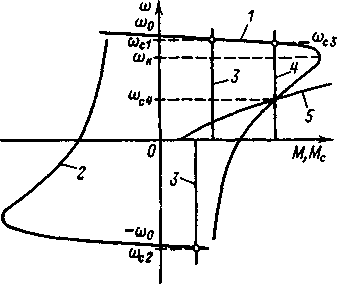Рис.4.13. К анализу статической устойчивости электропривода

Графически условие (4.28) определяется точкой пересечения механической характеристики двигателя =f(М) с механической характеристикой исполнительного механизма =f(М_с) (рис.4.13). На этом рисунке в качестве примера представлены механические характеристики 1 и 2 асинхронного двигателя для двух направлений вращения его магнитного поля, а также ряд механических характеристик различных исполнительных механизмов (3-5). Характеристика 3, как было показано в гл.1, соответствует механизму с активной полезной нагрузкой, например подъемной лебедке. При >0, что соответствует подъему груза, пересечение этой характеристики с механической характеристикой двигателя дает точку статического режима _c1, в которой двигатель, работая в двигательном режиме, преодолевает активный полезный момент и реактивный момент механических потерь. При противоположном направлении вращения (<0) характеристика 3, пересекаясь с характеристикой двигателя 2, дает точку статического режима _с2. Здесь двигатель работает в режиме рекуперативного торможения и его тормозной момент совместно с реактивным моментом механических потерь уравновешивает движущий момент полезной нагрузки.

Характеристика 4 пересекается с механической характеристикой двигателя в двух точках, чему соответствуют две скорости _с3 и _с4, при которых выполняется условие статического равновесия (4.28). Однако устойчивым это равновесие является только при скорости _с3. Незначительное отклонение скорости от _с4 вниз дает уменьшение момента двигателя, и в соответствии с (4.27) появляется динамический момент отрицательного знака, вызывающий дальнейшее снижение скорости. Аналогичное отклонение скорости вверх от _с4 приводит, напротив, к увеличению момента двигателя и появлению положительного динамического момента, что вызывает дальнейшее возрастание скорости вплоть до =_с3. При этом значении скорости динамические моменты, возникающие при любом малом отклонении скорости, направлены на уменьшение возникшего отклонения скорости и возвращают электропривод в точку устойчивого равновесия. Увеличение момента нагрузки вплоть до значения, соответствующего критическому моменту двигателя, приводит к слиянию точек устойчивого и неустойчивого равновесия в одну точку неустойчивого равновесия =_к=₀(1-s_k), поэтому участок механической характеристики асинхронного двигателя при <_к обычно называют неустойчивым.

Условия возникновения динамического момента при отклонениях от точки статического равновесия зависят как от формы характеристики двигателя, так и от вида характеристики исполнительного механизма. На рис.4.13 показана механическая характеристика вентилятора 5, пересекающая характеристику двигателя в точке _с4. Путем аналогичного анализа можно установить, что благодаря более значительным изменениям момента нагрузки, чем момента двигателя, возникающие при отклонениях скорости от _с4 динамические моменты возвращают систему к скорости _с4 и равновесие становится устойчивым.

Из изложенного следует, что при М_с=const устойчивость статического режима работы зависит от знака жесткости статической механической характеристики двигателя. Условие устойчивости: _ст=dM/d<0. Если момент механизма зависит от скорости, то его механическая характеристика также обладает определенной жесткостью _мех=dM_c/d, при этом условие статической устойчивости принимает вид

Следует иметь в виду, что приведенные рассуждения и полученные условия устойчивости статического режима работы справедливы только для электроприводов, у которых статическая и динамическая механические характеристики совпадают, например, в случае, когда T_э=0. В общем случае устойчивость статического режима работы электропривода определяется динамической жесткостью механической характеристики и параметрами механической части привода, поэтому она должна устанавливаться на основании анализа корней характеристического уравнения системы или частотными методами теории автоматического регулирования.