3.14. Режим динамического торможения асинхронного двигателя

Механическая характеристика на рис.3.42,а при f₁=0 соответствует режиму динамического торможения асинхронного двигателя при его независимом возбуждении со стороны статора постоянным током I₁. Такой режим возможен при питании от преобразователя частоты со свойствами источника тока при задании u_зч=0 (f₁=0). Однако в современном асинхронном электроприводе режим динамического торможения чаще используется для останова двигателя, получающего питание от сети, либо для регулирования скорости. Для осуществления режима динамического торможения асинхронный двигатель отключается от сети переменного тока и включается по схеме, приведенной на рис.3.44,а. При этом обмотка статора может быть соединена либо в звезду, либо в треугольник, в отдельных случаях подключают свободную фазу к одной из работающих, как показано на рис.3.44,a штриховой линией. Применяются и более сложные переключения обмоток статора для увеличения результирующей МДС при данном токе I_п или напряжении U_п.

Так как постоянный ток I_п не зависит от тока ротора в статике, а при достаточно большом R_1доб и в динамике, режим динамического торможения является частным случаем питания от источника тока. Поэтому проведенный анализ условий работы и характеристик двигателя при питании от источника тока полностью применим и к режиму динамического торможения при f₁=0 и ₀=0. В связи с наличием различных схем включения обмоток статора для использования полученных в §3.13 соотношений необходимо установить связь между трехфазным током I₁ для которого эти соотношения получены, и постоянным током I_п в схеме динамического торможения. Условием эквивалентности является равенство МДС, создаваемых постоянным током I_п при данной схеме соединения обмоток и переменным током I₁.

О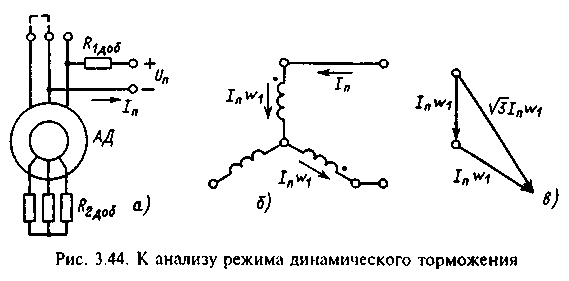 пределение эквивалентного тока I₁=I_экв, исходя из этого условия, не представляет затруднений. В качестве примера на рис.3.44,б приведена наиболее употребительная схема при соединении обмоток в звезду, а на рис.3.44,в векторным суммированием МДС фаз обмоток определена результирующая МДС для этой схемы:

Эквивалентный ток определим, приравняв F_п амплитуде результирующей МДС, создаваемой трехфазным током I₁=I_экв:

Следовательно, в данной схеме

Подставляя в полученные в §3.13 соотношения I₁=I_экв и ₀=0, можно использовать их для анализа динамического торможения. Выражение абсолютного скольжения для режима динамического торможения имеет вид

В соответствии с выражением критического момента М_к1 и критического скольжения s_k1 в (3.109) для режима динамического торможения можно записать

Нетрудно видеть, что введение добавочных резисторов в цепь ротора при динамическом торможении снижает жесткость рабочего участка, так же, как и при двигательном режиме.

3.15. Электромеханические свойства синхронных двигателей

Синхронные двигатели, как правило, исполняются с явнополюсным ротором, на котором размещается обмотка возбуждения. Питание обмотки возбуждения осуществляется через контактные кольца от источника постоянного напряжения, а трехфазная обмотка статора подключается к сети переменного тока, как показано на рис.3.46,a. Двухфазная модель такой машины представлена схемой на рис.3.46,б. Здесь обмотки фаз статора питаются симметричной двухфазной системой напряжений

Обмотка возбуждения размещена на оси d явнополюсного ротора и подключена к источнику постоянного напряжения и_в. Уравнения электромеханической характеристики, записанные для реальных переменных в осях а, р, d, q, имеют вид

О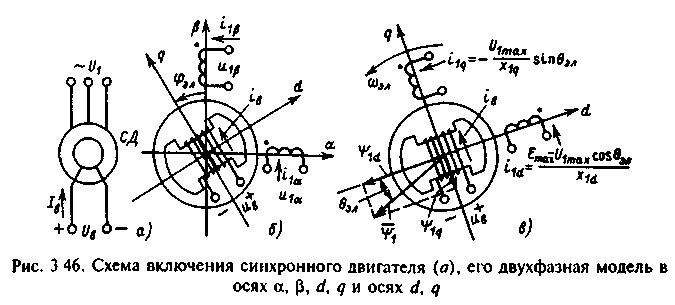 собенностью рассматриваемого двигателя является синхронное вращение ротора с вращающимся полем статора. При работе в двигательном режиме ротор отстает от поля статора на угол _ЭЛ=_0эл-_эл=_0эл·t-_эл, поэтому наиболее удобный для анализа вид уравнения механической характеристики имеют в осях d, q. Вначале преобразуем напряжения u_1, м_1 к осям d, q с помощью формул прямого преобразования (2.15):

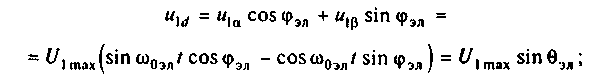
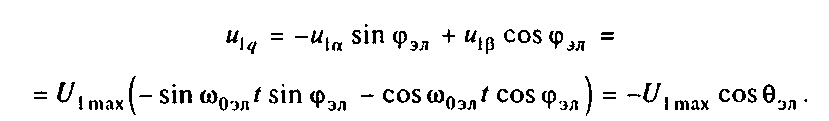
Подставив преобразованные выражения напряжений в (3.113) и дополнив эту систему уравнением электромагнитного момента, получим уравнения механической характеристики синхронного двигателя в осях d, q:

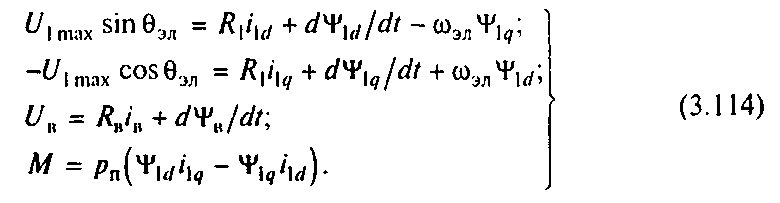
Схема синхронного двигателя в осях d, q представлена на рис.3.46,в. В соответствии с этой схемой записываем уравнения потокосцеплений, учитывая, что вследствие явнополюсности ротора

Уравнения (3.114) нелинейны в связи с наличием произведений переменных, поэтому для строгого анализа динамических режимов синхронного двигателя следует использовать цифровые или аналоговые вычислительные машины. Приближенное уравнение динамической механической характеристики может быть найдено с помощью угловой статической характеристики двигателя, для получения которой положим в (3.114) d/dt=0 и _эл=_0эл, пренебрежем активным сопротивлением статора R₁0, примем, что обмотка возбуждения получает питание от источника тока и во всех режимах i_в=-I_в=const, при этом система (3.114) примет вид

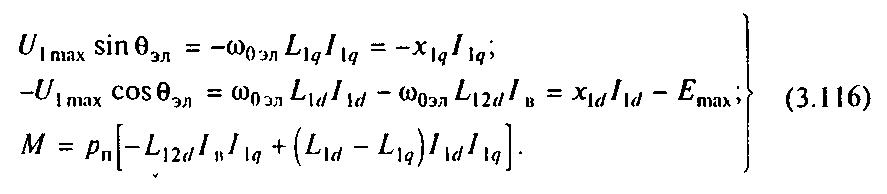
Из первого и второго уравнений (3.116) определяются токи статора:

Подставляя выражения токов в третье уравнение (3.116) и учитывая, что L_12dI_B=E_mах/_0эл, после преобразований получаем уравнение угловой характеристики двухфазного явнополюсного синхронного двигателя в виде

Произведем замену переменных двухфазной машины переменными трехфазной с помощью (2.37) и перейдем к эффективным значениям ЭДС и напряжения. В результате получим известное уравнение угловой характеристики трехфазного явнополюсного синхронного двигателя:

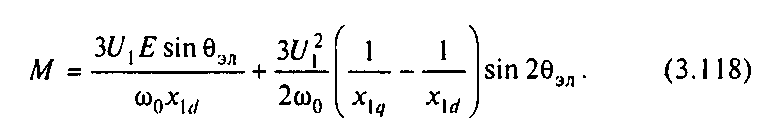
Уравнение (3.118) свидетельствует о том, что электромагнитный момент синхронного двигателя состоит из двух составляющих, первая из которых обусловлена взаимодействием вращающегося поля статора с полем возбужденного ротора, а вторая представляет собой реактивный момент, обусловленный явнополюсным исполнением ротора. Вследствие явнополюсности энергия магнитного поля максимальна при любом из двух возможных соосных с полем статора положений ротора, что и определяет зависимость реактивного момента от двойного угла _эл.

Примерный вид угловой характеристики М=f(_эл) показан на рис.3.47,а. Рассматривая ее, можно убедиться, что увеличение угла _эл вызывает рост электромагнитного момента вначале в зависимости, близкой к линейной. При _ЭЛ> 45° темп нарастания момента быстро снижается, и после достижения максимума М_mах дальнейшее возрастание угла  влечет за собой уменьшение момента двигателя. Без учета явнополюсности ротора максимум момента наступает при _ЭЛ=90°.

В номинальном режиме работы, когда двигатель развивает номинальный электромагнитный момент М_ном, угол _эл обычно составляет _ЭЛном=2030°. Этим обстоятельством определяется перегрузочная способность синхронного двигателя, которая лежит в пределах =М_тaх/М_ном=23. Рассмотрение рис.3.47,а,б позволяет заключить, что реактивный момент увеличивает крутизну рабочего участка угловой характеристики и несколько повышает перегрузочную способность двигателя.

П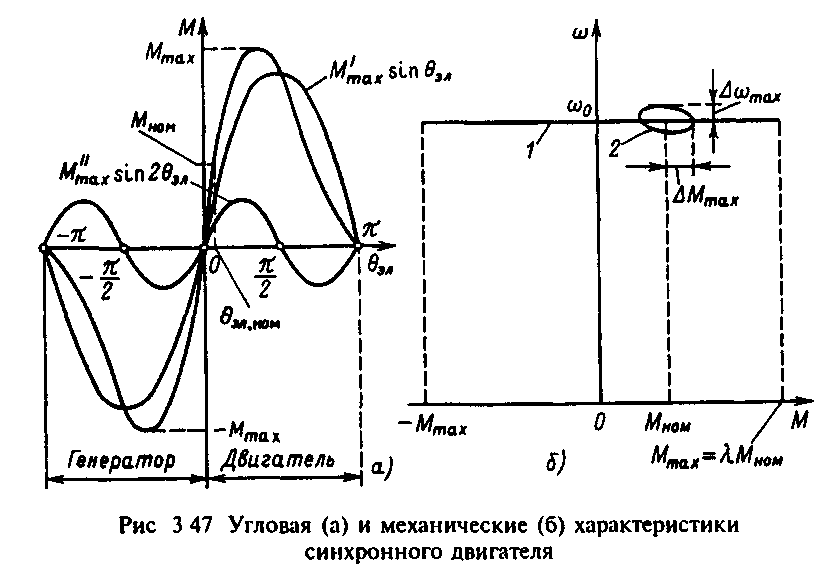 ерегрузочная способность синхронного двигателя менее чувствительна к понижению напряжения сети, чем у асинхронного двигателя, что относится к числу его важных достоинств. Этот вывод следует непосредственно из (3.118), если учесть, что реактивный синхронный момент, зависящий от квадрата напряжения, мало влияет на перегрузочную способность, а основная составляющая момента зависит от напряжения U₁ линейно, так как ЭДС машины Е определяется током возбуждения I_в.

Механизм образования синхронного момента виден на рис.3.46,в. На этом рисунке обозначены все токи, определяющие направление вектора потокосцепления статора связанного с осью вращающегося магнитного поля машины. Вектор определяется геометрической суммой потокосцеплений обмотки статора по оси d

и по оси q _1q=L_1qI_1q. В соответствии с (3.117) на рисунке приведены зависимости токов I_1d и I_1q от угла _эл Рассматривая рисунок, можно установить, что при идеальном холостом ходе I_1q=0 и вектор совпадает с осью ротора d. Под нагрузкой ось ротора d и составляющая вектора потокосцепления _1d, которая в основном определяется током возбуждения, отстают от оси вращающегося магнитного поля, определяемой положением вектора на угол _ЭЛ. Между постоянным магнитом, которым является возбужденный ротор, и вращающимся магнитным полем возникают силы взаимодействия. При малых углах _ЭЛ эти силы при увеличении _ЭЛ возрастают по закону, близкому к линейному. Нетрудно видеть, что рассмотренное электромагнитное взаимодействие вполне подобно механической упругой связи между полем ротора и результирующим полем машины. Поэтому по главным динамическим свойствам синхронный двигатель подобен упругим механическим системам.

Рабочий участок угловой характеристики М=f(_эл) можно с достаточной для многих задач инженерной практики точностью заменить линейной зависимостью М=k_эл, проходящей через точку номинального режима:

где с_эм - коэффициент жесткости упругой электромагнитной связи двигателя.

Дифференцируя (3.119), получаем приближенное уравнение динамической характеристики:

Как было установлено в гл. 1, момент упругого взаимодействия М₁₂ в двухмассовой линейной упругой системе

Дифференцирование этой зависимости дает уравнение, совпадающее по форме с (3.120), что еще раз подтверждает аналогию между электромагнитными взаимодействиями в синхронном двигателе и механическими в механической пружине. Этим определяется повышенная склонность синхронного двигателя к колебаниям, для устранения (или снижения) которой реальные синхронные двигатели снабжаются демпферной (пусковой) короткозамкнутой обмоткой. Эта обмотка выполняется в виде беличьей клетки на полюсах ротора и при возникновении колебаний скорости ротора, т. е. скольжения, создает асинхронный момент. Пренебрегая влиянием электромагнитной инерции на асинхронный момент, результирующий момент синхронной машины в динамических процессах можно приближенно представить в виде суммы синхронного М_син и асинхронного моментов М_ас:

где

С учетом (3.120) уравнение механической характеристики синхронного двигателя в операторной форме примет окончательный вид

Структурная схема электромеханического преобразования энергии, соответствующая (3.122), представлена на рис.3.48,а. При р=0 из (3.122) получаем уравнение статической механической характеристики =₀=const. Следовательно, в статическом виде изменения нагрузки на валу двигателя не приводят к изменениям скорости, так как модуль статической жесткости равен бесконечности. Это справедливо лишь в пределах перегрузочной способности двигателя, определяемой угловой характеристикой на рис.3.47,д. При возрастании нагрузки до значений, превышающих М_max=М_НОМ, двигатель выпадает из синхронизма. Статическая механическая характеристика синхронного двигателя соответственно имеет вид, показанный на рис.3.47,б (прямая 1).

В динамических режимах механическая характеристика синхронного двигателя, как следует из (3.122), не является абсолютно жесткой. В установившемся динамическом режиме вынужденных колебаний изменениям момента с амплитудой М_mах и соответствующим изменениям угла _эл по (3.122) соответствуют определенные амплитуды _mах колебаний скорости и динамическая механическая характеристика имеет вид эллипса (рис 3.47,б, кривая 2). Передаточная функция динамической жесткости определяется по рис.3.48,а:

Соответственно АФХ, АЧХ и ФЧХ динамической жесткости определяются соотношениями

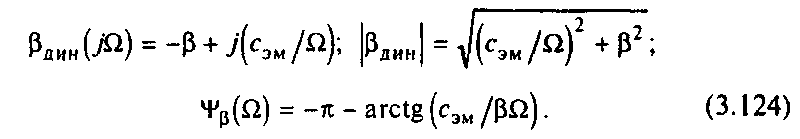
Логарифмические частотные характеристики динамической жесткости представлены на рис.3.48,б. Низкочастотная асимптота ЛАЧХ динамической жесткости имеет наклон -20 дБ/дек, поэтому модуль жесткости характеристики синхронного двигателя при возрастании частоты быстро убывает, стремясь к значению, определяемому жесткостью рабочего участка асинхронной характеристики M=f(), а фазовый сдвиг () изменяется от –3/2 до -.

Ч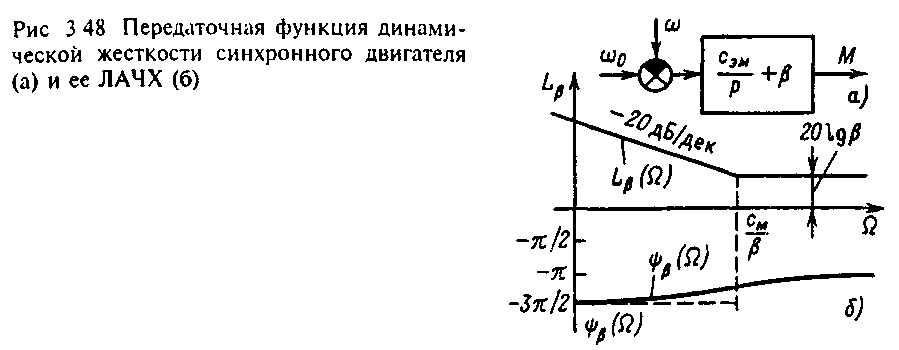 астотные характеристики динамической жесткости свидетельствуют о том, что соответствующая статическим режимам абсолютно жесткая характеристика синхронного двигателя для анализа динамических процессов неприменима. Динамические механические характеристики, соответствующие даже сравнительно медленным изменениям момента двигателя, могут существенно отличаться от статических.

Важным достоинством синхронного двигателя является возможность регулирования реактивной мощности путем воздействия на ток возбуждения I_в. Выражение для тока 1_1d (3.117) свидетельствует о том, что при прочих равных условиях этот ток и его знак определяются током возбуждения I_в, которому пропорциональна при принятых для обобщенной машины допущениях ЭДС Е_max. Ток I_1q не зависит от тока возбуждения, поэтому влияние возбуждения двигателя на условия преобразования энергии можно проанализировать с помощью векторных диаграмм, соответствующих системе (3.116) при _ЭЛ=const, представленных на рис.3.49.

П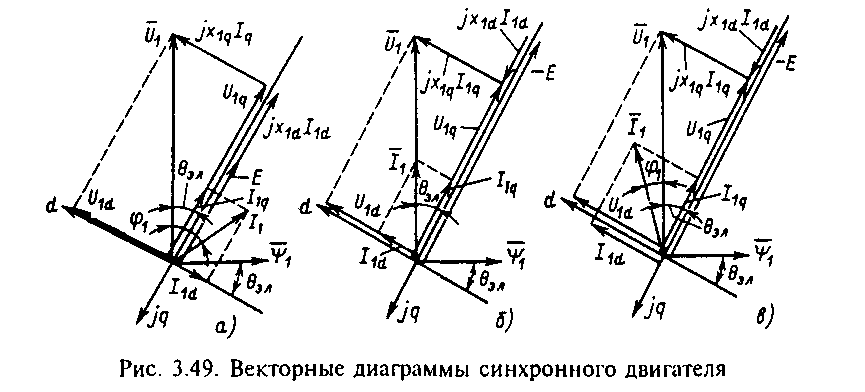 ри относительно небольшом токе возбуждения E_max<U_max·cos _ЭЛ и ток I_1d направлен в отрицательную сторону оси d (рис.3.49, a), при этом ток статора отстает от приложенного напряжения на угол ₁ и из сети потребляется реактивная мощность. Это потребление тем больше, чем меньше ток возбуждения. Увеличивая ток возбуждения, можно изменить направление тока I_1d и установить такое его значение, при котором вектор тока статора совпадает по направлению с напряжением сети (рис.3.49,б), при этом двигатель потребляет из сети (или отдает в сеть) только активную мощность, работая с cos ₁=1. Дальнейшее увеличение тока возбуждения и ЭДС двигателя Е приводит к работе двигателя с опережающим cos ф₁ и отдаче реактивной мощности в сеть (рис.3.49,в).

Из сравнения векторных диаграмм на рис.3.49 можно заключить, что при _ЭЛ=const увеличение тока возбуждения и ЭДС E вызывает увеличение активной составляющей тока рост активной мощности, а следовательно, и момента двигателя. При неизменном моменте двигателя увеличение тока возбуждения приводит к уменьшению угла _эл, а работа при ₁=0 соответствует минимальному току статора I₁ потребляемому двигателем при этом моменте. Как следует из (3.118), увеличение тока возбуждения I_в и ЭДС Е приводит к увеличению перегрузочной способности синхронного двигателя. Поэтому форсирование возбуждения при пиках нагрузки на практике используется для повышения устойчивости работы двигателя в этих режимах.