3.8. Динамические свойства электромеханического преобразователя с последовательным возбуждением

П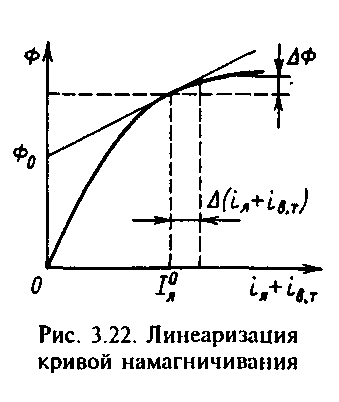 олученное в §3.6 математическое описание процессов электромеханического преобразования энергии в двигателе с последовательным возбуждением содержит произведения переменных, поэтому использовать его для анализа динамических свойств преобразователя можно лишь с помощью ЭВМ. Однако общие закономерности, основные динамические свойства электромеханического преобразователя с последовательным возбуждением могут быть выявлены аналитическим путем, если осуществить линеаризацию уравнений механической характеристики (3.50) в окрестности точки статического равновесия.

Так как линеаризация осуществляется в окрестности точки статического равновесия, кривую намагничивания следует аппроксимировать касательной в точке I_я⁰, Ф⁰, как показано на рис.3.22, при этом Ф=Ф₀+k'_ф(i_я+i_вт) и первые два уравнения системы (3.50) могут быть преобразованы к виду

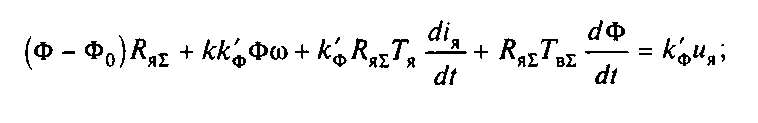
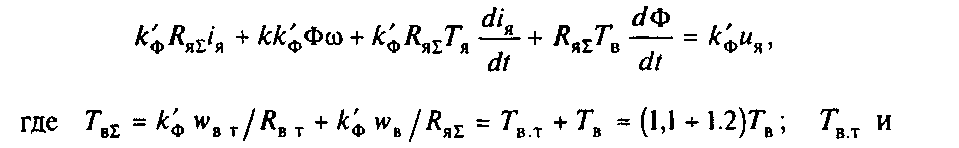
T_в- постоянные времени соответственно эквивалентного контура вихревых токов (см. рис.3.15,б) и обмотки возбуждения. Вычтя почленно из первого уравнения второе, получим более удобный для решения вид системы (3.50):

Линеаризуем систему (3.57) путем разложения в ряд Тэйлора в окрестности точки статического равновесия, обозначим d/dt=р, получим

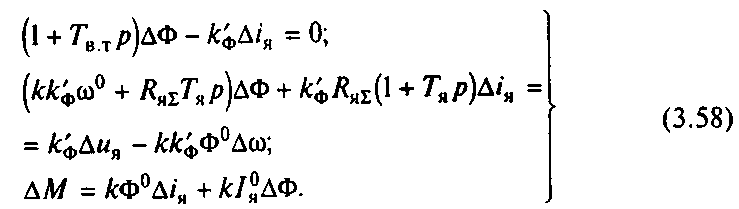
Решив систему (3.58) относительно Д/_я и М, получим линеаризованные уравнения электромеханической и механической характеристик двигателя в виде

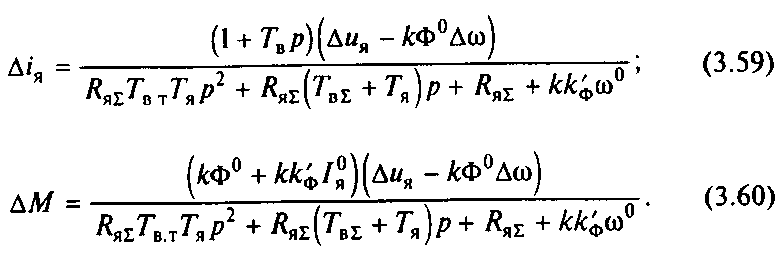
Уравнения (3.59) и (3.60) характеризуют основные динамические особенности преобразователя с последовательным возбуждением при условии ограничения отклонения переменных от точки статического равновесия узкими пределами. Сравнивая их, можно установить, что наличие контура вихревых токов определяет более значительные колебания тока, чем момента при тех же условиях. Это различие существенно усиливается, если не учитывать индуктивности рассеяния якорной цепи, положив Т_я=0. При этом порядок числителя и порядок знаменателя (3.59) становятся одинаковыми, что свидетельствует о возможности изменения тока якоря скачком и существенно искажает действительный характер процессов. Поэтому во всех случаях, когда ставится задача оценки характера изменения тока и его значения в том или ином динамическом режиме, следует пользоваться уравнением (3.59), не прибегая к дополнительным упрощениям.

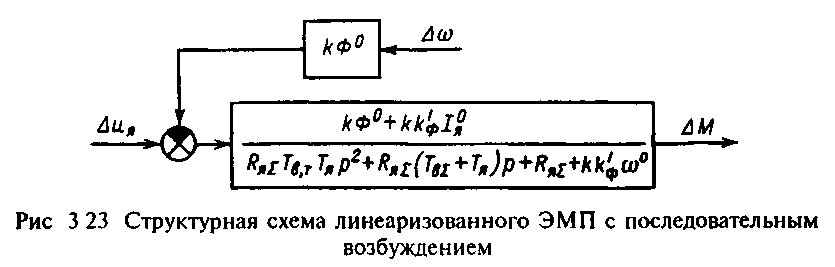
Структурная схема линеаризованного электромеханического преобразователя с последовательным возбуждением, соответствующая (3.60), представлена на рис.3.23. С помощью этой схемы определим передаточную функцию динамической жесткости механической характеристики:

Уравнение (3.61) свидетельствует о том, что динамическая жесткость в данном случае существенно зависит от положения точки статического равновесия на механической характеристике двигателя. При этом следует иметь в виду, что каждой точке статической характеристики соответствуют не только различные значения Ф°, I_я°, ⁰, но также и различные значения таких параметров, как T_в и k'_ф. При уменьшении момента двигателя по сравнению с номинальным (М°<М_ном) коэффициент k'_ф возрастает и при уменьшении потока до значений, соответствующих линейной части кривой намагничивания, становится равным коэффициенту k'_фmах=k'_ф [см. рис.3.16 и формулы (3.53) и (3.54)]. При дальнейшем уменьшении момента и потока k_ф остается постоянным, соответственно максимально и постоянно значение T_в. В области перегрузок (М°>М_ном) магнитная цепь двигателя насыщается, соответственно k'_ф и T_в принимают достаточно малые значения.

Если учесть, что Т_я и T_ВТ при I°_я<I_ном намного меньше, чем T_B и их произведение в (3.61) можно приближенно принять равным нулю, то для приближенных оценок получаем удобную формулу:

где

- модуль статической жесткости;

- эквивалентная электромагнитная постоянная

якорной цепи двигателя.

Формула (3.62) аналогична по форме формуле динамической жесткости двигателя с независимым возбуждением (3.44), но по существу отличается непостоянством модуля и эквивалентной электромагнитной постоянной в различных точках статической характеристики при I°_я<I_ном. Если магнитная цепь двигателя ненасыщенна, т. е. k_ф=k'_ф=const, то k'_фI°_я=Ф°, и модуль статической жесткости определяется соотношением

из которого следует, что с уменьшением нагрузки статическая жесткость механической характеристики уменьшается весьма быстро как из-за уменьшения потока Ф°, так и из-за возрастания скорости °. Модуль динамической жесткости при этом дополнительно снижается за счет электромагнитной инерции, характеризуемой постоянной времени Т_э так же, как и у двигателя с независимым возбуждением. При сопоставлении необходимо иметь в виду, что сумма T_в+Т_я при ненасыщенной машине намного превосходит значение Т_я для двигателя с независимым возбуждением, но включение обмотки возбуждения в силовую цепь приводит к тому, что T_э зависит от скорости ⁰ и существенно снижается при увеличении скорости. В области насыщения при I°_я>I_ном k'_ф0 и Т_В - стремится к значению, соответствующему индуктивности рассеяния обмотки возбуждения, при этом =k²Ф²/R_Я и Т_э=Т_я=L_Я, где L_я- суммарная индуктивность рассеяния якорной цепи. Таким образом, в области перегрузок динамические свойства двигателя с последовательным возбуждением практически совпадают с рассмотренными выше свойствами двигателя с независимым возбуждением.

Линеаризованные характеристики двигателя с последовательным возбуждением (3.59) и (3.60) могут быть использованы для анализа установившихся колебательных режимов электромеханических систем с двигателем последовательного возбуждения, а также для проверки устойчивости и качества замкнутых систем регулирования с таким двигателем при малых отклонениях от положения статического равновесия.