2.8. Физика атомного ядра и элементарных частиц

Строение и свойства атомных ядер. Состав ядра: протоны, нейтроны. Основные характеристики нуклонов и ядер. Изотопы. Понятие о ядерных силах. Масса и энергия связи в ядре. Средняя энергия нуклонов и её зависимость от массового числа. Неустой-чивость тяжёлых ядер по отношению к некоторым типам распада.

Радиоактивность. Ядерные реакции. Сущность явления радиоактивности. Типы радиоактивного распада. Основные харак-теристики -распада, -распада. Спектр -частиц. Нейтрино, -излу-чения радиоактивных ядер. Дозы ионизирующего излучения.

Понятие о ядерных реакциях. Законы сохранения в ядерных реакциях. Деление тяжёлых ядер. Понятие об элементарных частицах. Современная картина мира.

3. Основные рабочие формулы

С КРАТКИМИ ПОЯСНЕНИЯМИ

3.1. Физические основы механики

1. Вектор скорости точки есть производная радиус-вектора движущейся точки по времени:

.

Радиус-вектор  вектор, проведённый из начала координат в данную точку.

2. Вектор ускорения точки

.

3. Проекции скорости на оси координат:

; .

4. Проекции ускорения на оси координат:

; .

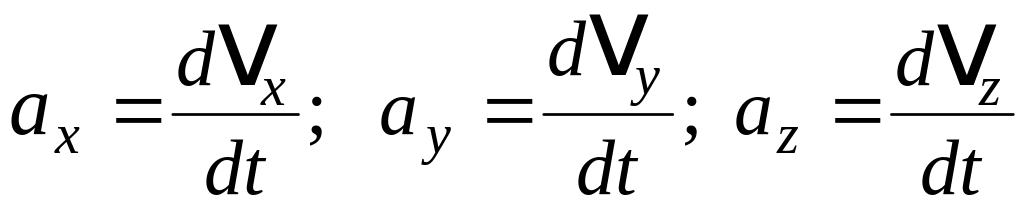5. Величина скорости

.

6. Вектор ускорения точки при криволинейном движении

,

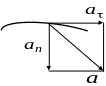
где  вектор тангенциального (касатель-ного) ускорения;  вектор нормального (центростремительного) ускорения.

Численные значения этих ускорений:

; ; ,

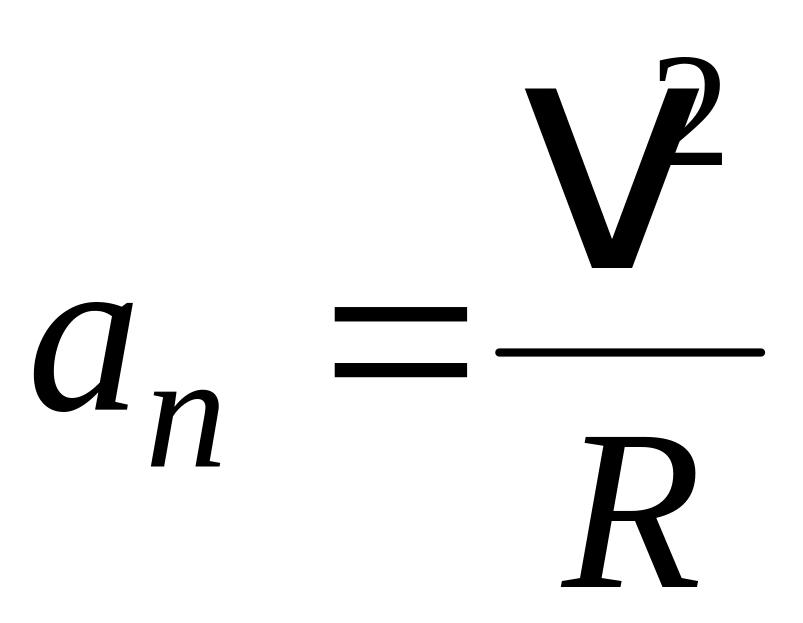где R – радиус кривизны траектории в данной точке.

7. Ускорение при прямолинейном движении (R =)

; .

8. Формулы для равномерного движения точки ( = const):

; .

9. Формулы для равномерного движения точки (a_τ = const):

; .

10. Угловая скорость тела есть первая производная угла по-ворота по времени:

.

11. Угловое ускорение тела есть первая производная угловой скорости по времени:

.

12. Формулы равномерного вращения (ω = const):

φ = ω  t; .

13. Число оборотов тела .

14. Частота вращения

или ,

где T – период вращения (время одного полного оборота); N – число оборотов, совершаемых телом за время t.

15. Угловая скорость тела, вращающегося равномерно,

.

16. Формулы равномерного вращения тела (ε = const):

; .

17. Пройденный путь, скорость и ускорения точки вращаю-щегося тела:

; ; ; ,

где R – расстояние точки от оси вращения.

18. Импульс материальной точки массой m, движущейся со скоростью , равен

.

19. Импульс системы материальных точек равен (по опре-делению) векторной сумме импульсов всех частиц, образующих систему:

.

20. Второй закон Ньютона:

,

где – результирующая сила, действующая на материальную точку.

21. Если масса постоянная, второй закон Ньютона может быть выражен формулой

,

где – ускорение.

22. Если сила постоянна по величине и направлению, то изменение импульса тела за конечный промежуток времени t равно произведению силы на время её действия:

или ,

где и – начальная и конечная скорости, разделённые проме-жутком времени t.

23. Сила упругости

,

где k – коэффициент упругости (в случае пружины  жёсткость).

24. Сила гравитационного взаимодействия

,

где – гравитационная постоянная; m₁, m₂ – массы взаимодейст-вующих тел; r – расстояние между ними.

25. Сила трения (скольжения). – сила нормального давления.

.

26. Закон сохранения импульса:

,

где n – число материальных точек (или тел), входящих в замкнутую систему.

27. Кинетическая энергия тела, движущегося поступательно,

.

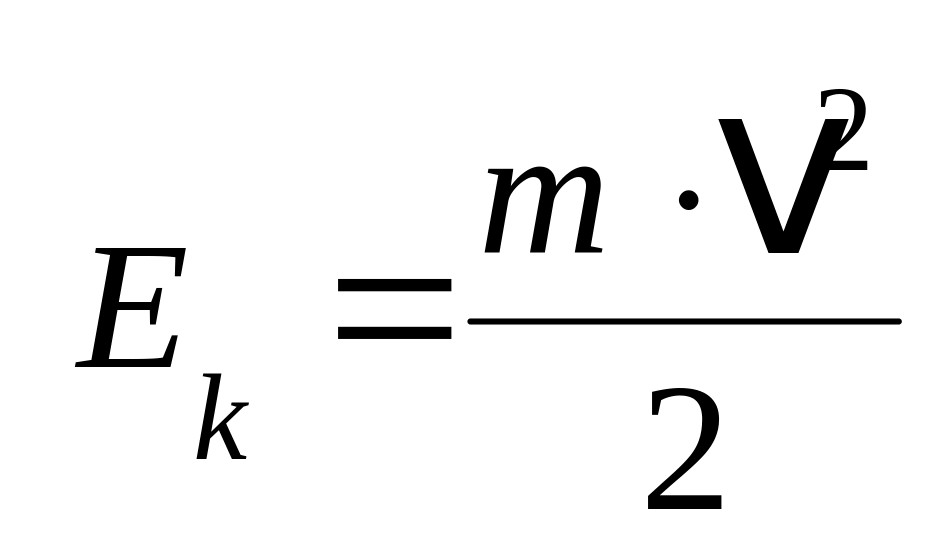28. Потенциальная энергия:

а) упругодеформированной пружины:

где k – жесткость пружины; x – абсолютная деформация.

б) гравитационного взаимодействия:

,

где  гравитационная постоянная; m₁ и m₂ – массы взаимодейст-вующих тел; r – расстояние между ними (тела рассматриваются как материальные точки).

в) тела, находящегося в однородном поле силы тяжести:

,

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, здесь R – радиус Земли).

29. Закон сохранения механической энергии:

.

30. Работа, совершаемая внешними силами, действующими на тело, и изменение его кинетической энергии связаны соотношением

.

31. Основное уравнение динамики вращательного движения относительно неподвижной оси z:

,

где результирующий момент внешних сил относительно оси z, действующих на тело; ε – угловое ускорение; момент инерции относительно оси вращения.

32. Момент инерции однородных тел вращения массовой m относительно их геометрических осей вращения:

а) тонкостенный цилиндр ;

б) сплошной цилиндр ;

в) шар .

33. Момент инерции однородного тонкого стержня длиной L относительно оси, проходящей через середину стержня перпенди-кулярно его длине,

.

34. Момент инерции тела относительно любой оси вращения и момент инерции относительно оси, параллельной данной и проходящей через центр масс тела, связаны соотношением (теорема Штейнера)

,

где a – расстояние между осями; m – масса тела.

35. Момент импульса вращающегося тела относительно оси вращения

,

где ω – угловая скорость тела.

36. Для материальной точки

,

где r – расстояние точки от оси, относительно которой определяется момент импульса; m – масса точки; – линейная скорость.

37. Работа постоянного момента силы , действующего на вращающее тело, находится по формуле

,

где φ – угол поворота тела.

38. Кинетическая энергия вращающегося тела

.

39. Кинетическая энергия тела, катящегося по плоскости без скольжения, равна

,

где  кинетическая энергия поступательного движения тела; – скорость центра масс тела;  кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.

40. Закон сохранения момента импульса: если суммарный момент внешних сил относительно некоторой оси равен нулю, то момент импульса системы относительно этой оси есть величина постоянная:

.