Задание 2.19.
В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 60 и 40 т. Тарифы перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей
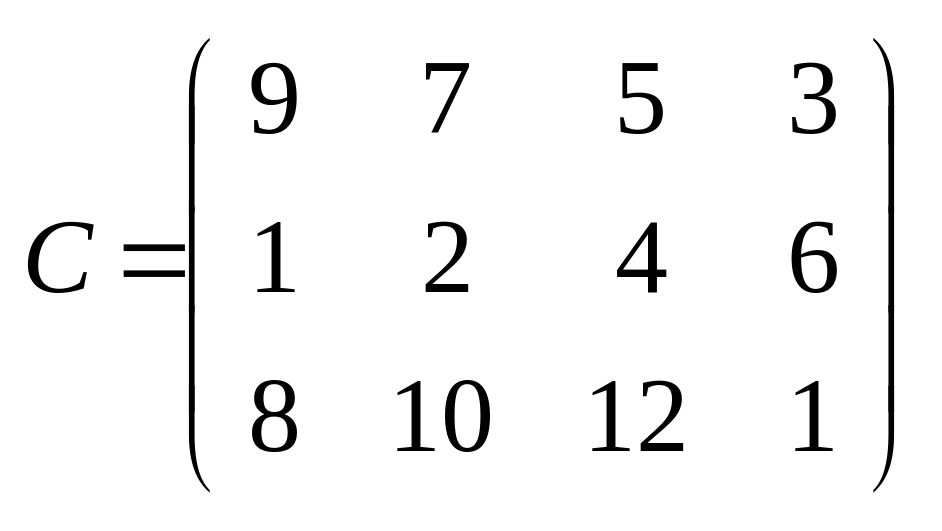
Составить такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.
Задание 2.20.
Компания имеет два товарных склада (А1 и А2) и трех оптовых покупателей (Bl, B2, ВЗ). Известно, что общий объем запасов на складах составляет 300 тыс. единиц продукции и совпадает с общим объемом заказов покупателей. Конкретные данные о загруженности каждого из складов (в тыс. ед.), потребности каждого покупателя (в тыс. ед.) и стоимости перевозки (тыс. руб./тыс. ед.) приведены в таблице. Минимизируйте общую стоимость перевозок.
|
Стоимость перевозок к потребителям |
Наличие |
|||
В1 |
В2 |
ВЗ |
|
||
Склады |
А1 |
8 |
5 |
6 |
120 |
А2 |
4 |
9 |
7 |
180 |
|
Запрос |
70 |
140 |
90 |
300 |
|
Задание 2.21.
Два торговых склада поставляют продукцию в четыре магазина. Издержки транспортировки продукции с торговых складов в магазины, наличие продукции на складах и потребности магазинов приведены в таблице.
|
Стоимость перевозок к потребителям |
Наличие |
||||
В1 |
В2 |
ВЗ |
В4 |
|
||
Склады |
А1 |
4 |
3 |
5 |
6 |
100 |
А2 |
8 |
2 |
4 |
7 |
200 |
|
Запрос |
50 |
100 |
75 |
75 |
300 |
|
Минимизируйте общую стоимость перевозок.
Задание 2.22.
Предположим, что нужно перевезти весь груз с трех складов в два пункта, причем весь груз должен быть перевезен во все пункты. В первый пункт должно быть перевезено 45 единиц груза, во второй — 79. На складах груз распределен следующим образом: на первом — 18, на втором — 75, на третьем — 31. Стоимость перевозки единицы груза со склада в пункт определяется таблице.
Пункт 1 |
Пункт 2 |
|
17 |
6 |
Склад 1 |
12 |
13 |
Склад 2 |
9 |
8 |
Склад 3 |
Требуется определить такую организацию перевозок, чтобы затраты на них были минимальными.
Задание 2.23. (Задача о расписании полетов)
Ежедневно авиалиния, которая принадлежит некоторой компании, осуществляет следующие перелеты между городами X и Y:
№ полета |
Отправление из X |
Прибытие в Y |
№ полета |
Отправление из Y |
Прибытие в X |
1 |
09.00 |
11.00 |
11 |
08.00 |
10.00 |
2 |
10.00 |
12.00 |
12 |
09.00 |
11.00 |
3 |
15.00 |
17.00 |
13 |
14.00 |
16.00 |
4 |
19.00 |
21.00 |
14 |
20.00 |
22.00 |
5 |
20.00 |
22.00 |
15 |
21.00 |
23.00 |
Требуется:
Организовать полеты «туда» и «обратно» так, чтобы минимизировать время простоя при условии, что каждому самолету требуется, по крайней мере, 1 ч для заправки.
Составить расписание полетов, совершаемых каждым из самолетов.
Представить найденное решение в виде диаграммы.
Выяснить сколько самолетов требуется для полетов по составленному расписанию.
Указания:
1. Вычислить по расписанию перелетов время простоя в каждом случае и записать результат в таблице:
П/в Х |
1 |
2 |
3 |
4 |
5 |
П/в Y |
11 |
12 |
13 |
14 |
15 |
11 |
23 |
24 |
5 |
9 |
10 |
1 |
21 |
22 |
3 |
9 |
10 |
12 |
22 |
23 |
4 |
8 |
9 |
2 |
20 |
21 |
2 |
8 |
9 |
13 |
17 |
18 |
23 |
3 |
9 |
3 |
15 |
16 |
21 |
3 |
4 |
14 |
11 |
12 |
17 |
21 |
22 |
4 |
11 |
12 |
17 |
23 |
24 |
15 |
10 |
11 |
16 |
20 |
21 |
5 |
10 |
11 |
16 |
22 |
23 |
2. Составить задачу целочисленного программирования о минимизации времени простоя и решить ее средствами Excel (аналогично решению Задания 25).
3. С помощью полученного решения составить схему полетов.
4. Выяснить по схеме полетов минимальное число самолетов, требуемых для организации перелетов.