1.3.3. Константи

Існує два види констант:

- звичайні - ціле або дробове число, рядок символів або окремий символ, логічне значення;

- іменовані - константа, повідомляється в розділі cost таким чином:

Ім’я _ константи = значення;

Приклад:

Н=10;

Сар =’ Корінь ’;

РІ=3.1415;

В результаті привласнення змінна набуває значення. У загальному вигляді оператор привласнення має вигляд:

Ім'я змінної := вираз;

1.3.4 Вирази

Вирази складаються з операндів і операторів. Оператори знаходяться між операндами. Операндами можуть бути константи і/або змінні. Оператори позначають наступні дії:

Таблиця 3 Оператори

Оператор	Дія
+	Складання
-	Віднімання
*	Множення
/	Ділення
DIV	Ділення без остачі
MOD	Обчислення залишку від ділення

1.3.5. Стандартні функції

Для виконання обчислень, які часто зустрічаються, і перетворень даних використовуються стандартні функції

Таблиця 4 Стандартних функції

Значення	Функція
x	ABS(x)
х2	SQR(x)
x	SQRT(x)
ex	EXP(x)
ln x	LN(x)
sin x	sin (x)
cos x	cos(x)
arctg x	arctan(x)

За допомогою цих функцій можна обчислити значення інших функцій.

SIN(X)/ COS(X) -

SQR(SIN(X) /COS(X)) -

SIN(SQR(X)) /COS(SQR(X)) -

Для зведення числа в речовинний або цілий ступінь використовується наступне математичне співвідношення:

exp(n*ln(x)) хn=en ^lnx

exp((1/n)*ln(x)) x^1/n

exp((m/n)*ln(x)) ^m=x^m/n

exp(n*ln(sin(x) /cos(x)))

exp(n*ln(ln(x)))

Якщо в арифметичних виразах є функції, що не входять до складу стандартних функцій, їх слід виразити через стандартні функції

Приклади записів арифметичних виразів для обчислення значення функції.

Приклад 1.

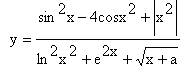
Y:=(SQR(SIN(X))-4*COS(SQR(X))+ABS(SQR(X))) / (SQR(LN(SQR(X)))+EXP(2*X)+SQRT(X+A))

Функції перетворення типів

Функції перетворення типів найчастіше використовуються в операторах, які забезпечують введення і виведення інформації. Наприклад, для того щоб вивести в полі виведення значення змінної типу real, необхідно спочатку одержати зображення числа, яке є значенням цієї змінної. Це можна зробити за допомогою функції FloatToStr, яке повертає строкове представлення виразу дійсного типа, відміченого при виклику

Таблиця 5 Функції перетворення типів

Функція	Значення
Chr(n)	Символ ANSI з номером n
IntToStr(n)	Рядок, який є зображенням значення цілого
FloatToStr(n)	Рядок, який є зображенням значення дійсного n
StrToInt (s)	Ціле, зображенням якого є рядок s
StrToFloat (s)	Дійсне, зображенням якого є рядок s
Round(n)	Ціле, найближче до n
Trunc(n)	Ціла частина від n
Frac(n)	Дробова частина дійсного n
Int (n)	Ціла частина дійсного n