3. Логарифмическая производная

Пусть задана дифференцируемая функция . Тогда называют логарифмической производной этой функции. Ясно, что . Иногда бывает проще сначала найти логарифмическую производную.

Пример. Найдем производную функции . Сначала найдем логарифмическую производную этой функции –

Отюда следует

Теперь найдем производную функции :

4. Теорема Лагранжа

1. Минимумы и максимумы

Пусть функция определена в окрестности точки . Точка называется точкой локального максимума, если 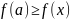для всех из достаточно малой окрестности точки . Если выполняется неравенство для всех из достаточно малой окрестности точки , то a называется точкой локального минимума. Точка локального минимума или локального максимума называется точкой локального экстремума.

Точек локального экстремума на заданном отрезке может быть сколь угодно много (в частности, бесконечно много). Значений в этих точках может быть также сколь угодно много. Но наибольшее (наименьшее) значение функции на заданном множестве может быть только одно. Каждая точка интервала, в которой достигается наибольшее значение (наименьшее значение) на этом интервале автоматически будет точкой локального максимума (локального минимума), но обратное неверно (см. рис.).

Теорема Ферма; необходимое условие экстремума. Пусть - точка локального экстремума функции , причем эта функция определена в окрестности точки и имеет в этой точке производную. Тогда

Доказательство. Предположим, что -- точка локального максимума. Тогда для имеем и . Следовательно, . Но этот правый предел совпадает с двусторонним пределом. Отсюда . Аналогично, рассматривая левый предел, т.е. налагая условие , получим, что . Из последних двух неравенств следует равенство . □

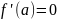Теорема Ролля. Пусть функция непрерывна на отрезке и дифференцируема на интервале , а в концах отрезка принимает одинаковое значение. Тогда найдется точка такая, что .

Доказательство. Пусть -- точки в которых функция достигает своих наименьшего и наибольшего значений (теорема Вейерштрасса). Если не является концевой точкой отрезка , то -- искомая точка по теореме Ферма.

Аналогично рассуждаем в случае, когда 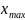не является концевой точкой. Итак, осталось разобрать случай, когда обе точки -- концевые. Тогда , и поэтому функция постоянна на отрезке , ибо любое значение лежит между . В этом случае в качестве c можно взять любую точку интервала . □

Механический смысл теоремы Ролля: если материальная точка, двигаясь на оси, возвратилась в исходную точку, то найдется момент времени, в котором ее мгновенная скорость была равна нулю. Геометрический смысл теоремы Ролля состоит в том, что если концы гладкой кривой лежат на одном и том же уровне относительно некоторой прямой, то найдется точка на этой кривой, касательная в которой параллельна заданной прямой.

Теорема Лагранжа. Пусть функция непрерывна на отрезке и дифференцируема на интервале . Тогда найдется точка такая, что

или

Доказательство. Рассмотрим вспомогательную функцию и применим к ней теорему Ролля. Это можно сделать, так как . Тогда получаем точку с условием , т.е.

Механический смысл теоремы Лагранжа: -- если материальная точка движется на оси некоторый конечный отрезок времени, то найдется промежуточный момент времени, в котором ее мгновенная скорость была равна средней скорости. Геометрический смысл теоремы Лагранжа состоит в том, что если через концы гладкой кривой провести секущую ℓ , то найдется точка на этой кривой, касательная в которой параллельна прямой ℓ .

Обобщим теорему Лагранжа

Теорема Коши. Пусть функции f(x) и g(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), причем g'(x)≠ 0 для любой точки x∈ (a,b). Тогда найдется точка c∈ (a,b) такая, что

Доказательство такое же как и у теоремы Лагранжа, но следует взять вспомогательную функцию .